O-cresol Concentration Online Measurement Based On Near Infrared Spectroscopy Via Partial Least Square Regression

Zihao Chen; Niannian Zheng; Xiaoli Luan; Fei Liu

doi:10.3791/59077

JoVE Journal > Engineering

Engineering

O-cresol Concentration Online Measurement Based On Near Infrared Spectroscopy Via Partial Least Square Regression

Published: November 08, 2019

doi:

10.3791/59077

Zihao Chen¹, Niannian Zheng¹, Xiaoli Luan¹, Fei Liu¹

¹Key Laboratory for Advanced Process Control of Light Industry of the Ministry of Education, Institute of Automation,Jiangnan University

Summary

The protocol describes a method of predicting o-cresol concentration during the production of polyphenylene ether using near-infrared spectroscopy and partial least squares regression. To describe the process more clearly and completely, an example of predicting the o-cresol concentration during the production of polyphenylene is used to clarify the steps.

Abstract

Unlike macroscopic process variables, near-infrared spectroscopy provides process information at the molecular level and can significantly improve the prediction of the components in industrial processes. The ability to record spectra for solid and liquid samples without any pretreatment is advantageous and the method is widely used. However, the disadvantages of analyzing high-dimensional near-infrared spectral data include information redundancy and multicollinearity of the spectral data. Thus, we propose to use partial least squares regression method, which has traditionally been used to reduce the data dimensionality and eliminate the collinearity between the original features. We implement the method for predicting the o-cresol concentration during the production of polyphenylene ether. The proposed approach offers the following advantages over component regression prediction methods: 1) partial least squares regression solves the multicollinearity problem of the independent variables and effectively avoids overfitting, which occurs in a regression analysis due to the high correlation between the independent variables; 2) the use of the near-infrared spectra results in high accuracy because it is a non-destructive and non-polluting method to obtain information at microscopic and molecular scales.

Introduction

Near infrared (NIR) spectroscopy (NIRS) has gained wide acceptance as a fast, efficient, non-destructive, and non-polluting modern analytical technology; the method has been used during the past several years for product quality detection and analysis and chemical component measurement in industrial processes. The most essential specialty of the method is its ability to record spectra for solid and liquid samples without any pre-processing, making NIRS especially suitable for the direct and rapid detection and analysis of natural and synthetic products¹^,². Unlike traditional sensors that measure process variables (e.g., temperature, pressure, liquid level, etc.) at a macroscopic scale and inevitably suffer the external noise and background interference, NIRS detects the structural information of the chemical composition at microscopic and molecular scales. Thus, essential information can be measured more accurately and effectively than with other methods³^,⁴.

Polyphenyl ether, as one of the engineering plastics, are widely used due to its heat resistance, flame retardant, insulation, electrical properties, dimensional stability, impact resistance, creep resistance, mechanical strength and other properties⁵. More importantly, it is non-toxic and harmless compared to other engineering plastics. At present, 2,6-xylenol is one of the basic raw materials for the synthesis of polyphenylene ether, and it is usually prepared by catalyzed alkylation of phenol with methanol method⁶. There are two main products of this preparation method, o-cresol and 2,6-xylenol. After a series of separation and extraction steps, 2,6 xylenol is used to produce polyphenylene ether. However, trace amounts of o-cresol remain in 2,6-xylenol. O-cresol does not participate in the synthesis of polyphenylene ether and will remain in the polyphenylene ether product, resulting in a decrease in product quality or even the substandard. At present, most companies still analyze the compositions of complex organic mixtures such as liquid phase polyphenyl ether products containing impurities (e.g., o-cresol) by physical or chemical separation analysis such as chromatography⁷^,⁸. The separation principle of chromatography is the use of the mixture of compositions in the fixed phase and the flow phase in the dissolution, analysis, adsorption, desorption or other affinity of the minor differences in the performance. When the two phases move relative to each other, the compositions are separated by the above actions repeatedly in the two phases. Depending on the object, it usually takes a few minutes to a few tens of minutes to complete a complex material separation operation. It can be seen that the measurement efficiency is low.

Nowadays, the measurement of product quality and the advanced control technology based on this analysis for the modern fine process chemical materials industry is the key direction to further improve product quality. In the process industry of polyphenyl ether production, real-time measurement of o-cresol content in polyphenylene ether product is of great development significance. Chromatographic analysis clearly cannot meet the requirements of advanced control technology for real-time measurement of substances and signal feedback. Therefore, we propose the partial least squares regression (PLSR) method to establish a linear model between the NIRS data and the o-cresol concentration, which realize the online measurement of o-cresol content in the liquid polyphenylene ether product of outlet.

The pre-processing for NIRS plays the most important role prior to multivariate statistical modeling. NIRS wavenumbers in the NIR spectrum and the particle sizes of biological samples are comparable, so it is known for unexpected scatter effects that has influence on the recorded sample spectra. By performing appropriate pre-processing methods, these effects are easy to be eliminated largely⁹. The most commonly used pre-processing techniques in NIRS are categorized as scatter correction and spectral derivative methods. First group of methods includes multiplicative scatter correction, detrending, standard normal variate transformations, and normalization. The spectral derivation methods include the use of the first and second derivatives.

Prior to developing a quantitative regression model, it is important to remove the unsystematic scatter variations from the NIRS data because they have a significant influence on the accuracy of the predictive model, its complexity and parsimony. The selection of a suitable pre-processing method should always depend on the subsequent modeling step. Here, if the NIR spectral dataset does not follow the Lambert-Beer law, then other factors tend to compensate for the non-ideal behavior of the prediction for predicted components. The disadvantage of the existence of such needless factors leads to the increase of model complexity, even most likely, a reduction in the robustness. Thus, the application of spectral derivatives and a conventional normalization to the spectral data is an essential part of the method.

After spectral preprocessing, the NIRS data with a high signal-to-noise ratio and low background interference are obtained. Modern NIRS analysis provides the rapid acquisition of large amounts of absorbance over an appropriate spectral range. The chemical composition of the sample is then predicted by extracting the relevant variables using the information contained in the spectral curve. Generally, NIRS is combined with multivariate analysis techniques for qualitative or quantitative analyses¹⁰. A multivariate linear regression (MLR) analysis is commonly used for developing and mining the mathematical relationship between the data and the components in industrial processes and has been widely used in NIRS analysis.

However, there are two fundamental problems when implementing an MLR for preprocessed NIRS data. One problem is the variable redundancy. The high dimensionality of the NIRS data often renders the prediction of a dependent variable unreliable because variables are included that have no correlation with the components. These redundant variables reduce the information efficiency of the spectral data and affect the accuracy of the model. In order to eliminate the variable redundancy, it is essential to develop and maximize the correlation between the NIRS data and the predicted components.

Another problem is the issue of multicollinearity in the NIRS data. One of the important assumptions of multiple linear regression models is that there is no linear relationship between any of the explanatory variables of the regression model. If this linear relationship exists, it is proved that there is multicollinearity in the linear regression model and the assumption is violated. In multiple linear regressions, such as an ordinary least squares regression (OLSR), multiple correlations between the variables affect the parameter estimation, increase the model error, and affect the stability of the model. To eliminate the multilinear correlation between the NIR spectral data, we use variable selection methods that maximize the inherent variability of the samples.

Here, we propose to use the PLSR, which is a generalization of multiple linear regression that has been widely used in the field of NIRS¹¹^,¹². The PLSR integrates the basic functions of the MLR, canonical correlation analysis (CCA), and principal component analysis (PCA) and combines the forecasting analysis with a non-model data connotation analysis. The PLSR can be divided into two parts. The first part selects the components of the characteristic variables and the predicted components by partial least squares analysis (PLS). PLS maximizes the inherent variability of principal components by making the covariance of the principal components and predicted components as large as possible when extracting the principal components. Next, the OLSR model of o-cresol concentration is established for the principal components selected. PLSR is suitable for the analysis of noisy data with numerous independent variables that are strongly collinear and highly correlated and for the simultaneous modeling of several response variables. Also, PLSR extracts the effective information of the sample spectra, overcomes the problem of multicollinearity, and has the advantages of strong stability and high prediction accuracy¹³^,¹⁴.

The following protocol describes the process of using the PLSR model for measuring the o-cresol concentration using NIR spectral data. The reliability and accuracy of the model are evaluated quantitatively by using the determination coefficient (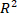), the prediction correlation coefficient (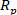) and the mean square prediction error of cross-validation (MSPECV). Moreover, to intuitively show the advantages of the PLSR, the evaluation indicators are visualized in several plots for a qualitative analysis. Finally, evaluation indicators of an experiment are presented in table format to quantitatively illustrate the reliability and precision of the PLSR model.

Protocol

1. NIR spectrum data acquisition with Fourier transform (FT)-NIR process spectrometer

Install the liquid phase optical fiber probe of the near-infrared spectrometer at the outlet of the polyphenyl ether product. And open the OPUS software on the upper computer connected to the instrument and start to configure the measurement.
Connecting to spectrometer
1. On the Measure menu, select the Optic Setup and Service command, or click the icon from the toolbar.
2. On the dialog that opens, click the Optical Bench tab.
3. Check whether the spectrometer settings are ok. If yes, close the dialog. If no, continue with step 4.
4. From the Configuration drop-down list, select the particular spectrometer type.
5. Enter the spectrometer’s IP address into the Optical Bench URL entry field.
6. Click the Connect button.
Setting up measurement parameters
1. On the Measure menu, select the Measurement command, or click the icon from the toolbar.
2. On the dialog that opens, define the measurement parameters on the different tabs.
  NOTE: Details on the individual measurement parameters are described in the OPUS Reference Manual.
3. Click the Accept & Exit button.
Storing experiment file
1. On the Measure menu, select the Advanced Measurement command. Then, click the Advanced tab.
2. On the dialog that opens, define the resolution as 4 cm^-1.
3. Define the number of scans as 16 scans in the Sample/Background Scan Time entry fields.
4. Define the path to automatically store the measuring data from 4,000 cm^-1-12,500 cm^-1.
5. Determine the data type for the result spectrum as Absorbance.
6. Click the Save button.
7. On the dialog that opens, define a name for the experiment file and save this name.
Measuring background spectrum
1. On the Measure menu, select the Advanced Measurement command.
2. Click the Optic tab.
3. On the dialog that opens, click the Aperture setting drop-down list and select the same value used to acquire a sample spectrum.
4. Click the Basic tab.
5. On the dialog that opens, click the Background Single Channel button.
Measuring sample spectrum
1. Place the sample into the optical path of the spectrometer. The way in which this is done depends on the spectrometer configuration.
2. On the Measure menu, select the Advanced Measurement command.
3. Click the Basic tab.
4. On the dialog that opens, define the sample description and sample form in the particular entry field. This information is stored together with the spectrum.
5. Click the Sample Single Channel button to start online measurement. And save the NIR spectrum of each scan as OPUS file.
Collect the polyphenylene samples every 6 h and test the o-cresol concentration with liquid chromatography in the laboratory of industry to obtain a chemical reference value.
NOTE: Laboratory staff of industry field take each polyphenyl ether sample from the outlet of the liquid phase polyphenyl ether. The o-cresol content in each sample was measured three times by liquid chromatography. Then, the mean value of the results of the three times analysis was taken as the reference value of the o-cresol content to reduce the accidental error.
Obtain 600 chemical reference values of o-cresol concentration in the laboratory. The calibration range of o-cresol concentration is from 42.1063 mg/1 g polyphenyl ether product to 51.6763 mg/1 g polyphenyl ether product.
Combine the NIR spectra at the given test times with the chemical reference values of the o-cresol concentration.
Use the software OPUS to read the original spectral set as shown in Figure 1.
1. On the File menu, click the Load File command.
2. On the dialog that opens, select the particular spectrum file.
3. Click the Open button. The spectrum is displayed in the spectrum window.

2. NIR spectroscopy data pre-processing

With the spectral preprocessing function in, obtain spectral dataset preprocessed with first-order derivative.
1. Open The Unscrambler which is a multivariate data analysis and experimental design software, select the Import command under File. Import the OPUS file as original NIR spectral dataset.
2. Select Transform command under Modify. And select the Savitzky Golay Derivatives under Derivatives.
3. Define the Samples and Variables as All Samples and All Variables in Scope. And define the number of Smoothing points as 13 and the Derivative as 1^st derivative in Parameters.
4. Click OK to start the derivative.
  CAUTION: The increase of smoothness can reduce the sharp fluctuations of the curve, reduce the noise effect but also weaken the characteristics of the curve and make the curve distorted. Therefore, the appropriate smoothness selected according to the observation of the actual fluctuation intensity of the curve and the effect after processing.
Perform vector normalization on the sample spectra to normalize the value of the absorbance.
1. Select the Normalization command under Modify.
2. Define the Samples and Variables as All Samples and All Variables in Scope.
3. Select Vector normalization in the Type.
4. Click OK to perform vector normalization.

3. Establishment of PLSR model

Creation of the NIR spectral data set
1. Open Uncrambler.exe, select Export under File with the Matlab files to export the preprocessed spectral data set into .mat File and to obtain the spectral data set X automatically with 2203 variables.
2. Obtain a complete NIR spectral dataset X (a matrix of 600 rows and 2203 columns) and the corresponding chemical reference values Y (a vector of 600 rows) in the form of .mat file for subsequent analysis and modeling.
Selection of the appropriate number of principal components
1. Open Matlab and import the .mat file containing the preprocessed near-infrared spectral data into the workspace by dragging the .mat file to the workspace.
  NOTE: The .mat file stores the near-infrared spectral data X as an independent variable and the o-cresol content of the product as a dependent variable in the form of two matrices.
2. Open the programmed .m file in the Editor. Click Open under the Editor option, select the compiled .m file in the file storage directory, and then click Confirm.
3. Extract 15 principal components according to the optimization objective of Equation 1 and the OLSR model between the extracted principal components and the predicted values of the o-cresol concentration with the program containing the command plsregress() in Matlab.
  [XL, YL, XS, YS, BETA, PCTVAR, MSE] = plsregress(X,Y,ncomp,’CV’,k);
  Consult the MATLAB help document to get the usage details and the return value.
  NOTE: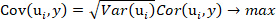 Equation 1
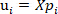  , and 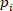is the i_thprincipal components of the NIR spectral data;
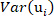  is the projection of the i_th principal components of the NIR spectral data;
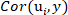  is the Pearson correlation coefficient for the i_th principal components and the o-cresol concentration.
4. Obtain the 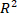value of the NIR spectral data and the predicted values for the different principal components using Equation 2.
  NOTE: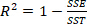 Equation 2
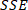  is the sum of squares due to error and is defined as ;
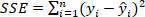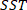  is the total sum of squares and is defined as ;
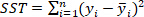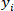  is the reference value of the o-cresol concentration of test dataset;
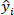  is the predicted value of the o-cresol concentration of test dataset;
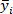  is the mean value of reference value of the o-cresol concentration of test dataset;
  is the number of samples of test dataset.
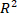5. Determine the values and the trend with increasing number of principal components as shown in Figure 2. Select 10 as the appropriate number of principal components with the 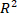value of 0.9917.
  NOTE: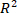 value is the proportion of the variance in the dependent variable that is predictable by the independent variables. The higher the 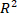value is, the higher the goodness-of-fit is and vice versa.
Validation of the goodness-of-fit and accuracy of the PLSR model with 10 principal components by using the command plsregress().
1. Repeat the modeling process with 10 principal components as steps 3.2.1-3.2.5 with 10 principal components.
2. Evaluate the model based on a 10-fold cross-validation using the plots of the percent variance explained in the NIR spectral data, the residuals, and the MSPECV.
3. Plot the percent variance explained in NIR spectral data, the residuals, and the MSPECV as Figures 3, 4, and 5.
4. Tabulate the evaluation indicators of 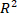,,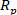 and MSPE of 10-fold cross validation for the PLSR model for a quantitative analysis as shown in Table 1.
  NOTE: The equations of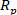 and MSPE are shown as Equation 3 and Equation 4.
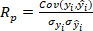  Equation 3
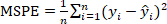  Equation 4
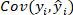  is the covariance of reference value and predicted value of o-cresol concentration; 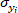is the standard deviation of reference value of o-cresol concentration;
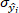  is the standard deviation of predicted value of o-cresol concentration.

Representative Results

The predicted value of o-cresol Impurity in polyphenyl ether products is obtained by PLSR-based near-infrared spectroscopy. Figure 2 and Figure 3 respectively show the reliability of the method in the feature selection stage from the curve of the decision coefficient and the error interpretation percentage increasing with the number of principal components.

Specifically, please note that in the selection of the principal components, in order to minimize the complexity of the model, generally, when the two indicators do not increase significantly with the number of principal elements, the subsequent principal elements with less information can be discarded. In this paper, according to the two curves, when 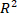is 0.9917, it is the threshold to discard subsequent principal components.

Visually test the accuracy and stability of the method for predicting the purity of o-cresol products by means in shown Figure 4 and Figure 5. Based on the training set and test set generated by the o-cresol samples obtained from industrial field and their corresponding near-infrared spectroscopy data, we compared the residual and mean square error of the predicted and reference values of the purity of polyphenyl ether products.

The residual here refers to the difference between the o-cresol content reference value and the PLSR model estimate (fitted value). Using the information provided by the residuals can help us examine the rationality of the established PLSR model assumptions and the reliability of collecting near-infrared spectral data. It is shown that PLSR method effectively reduce the residuals to an acceptable range. Moreover, the PLSR has a small fluctuation range from -0.2 to 0.2, while the calibration range is from 42.1063 mg/1 g polyphenyl ether product to 51.6763 mg/1 g polyphenyl ether product. The residual plot data let us conclude qualitatively that the PLSR for the measurement of the o-cresol content based on the NIR spectral data has high accuracy.

The cross-validation mean square error is a measure of the degree of difference between the reference and the predicted o-cresol content. This can help us evaluate the degree of change in the predictive data. The smaller the value of MSE, the better the accuracy of the predictive model describing o-cresol content. Figure 5 indicates that the MSPECV for the o-cresol concentration measurement based on the PLSR decrease as the number of principal components increases and reach an acceptable minimum at 10 principal components. Moreover, the error decreases significantly and the descent process is relatively stable. This proves that the PLSR results in high stability for the measurement of the o-cresol concentration using NIRS.

The model evaluation indicators for a 10-fold cross-validation are shown in Table 1. The 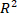of 0.98332 is pretty high for the PLSR, indicating that the model based on the PLSR well reflects the linear relationship between the NIR spectral data and the o-cresol concentration (i.e., the model has stronger explanatory power). The Pearson correlation coefficient 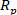is a statistic used to reflect the degree of linear correlation between two variables. The larger the absolute value of 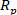, the stronger the correlation. This can help to quantitatively observe a linear correlation between the predicted o-cresol content value and the chemical reference value to confirm the reliability of the model. The mean relative prediction error (MRPE) of 0.01106 is very low for the PLSR and the prediction correlation coefficient 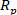of 0.99161 is large; therefore, the PLSR model is of great prediction stability and accuracy.

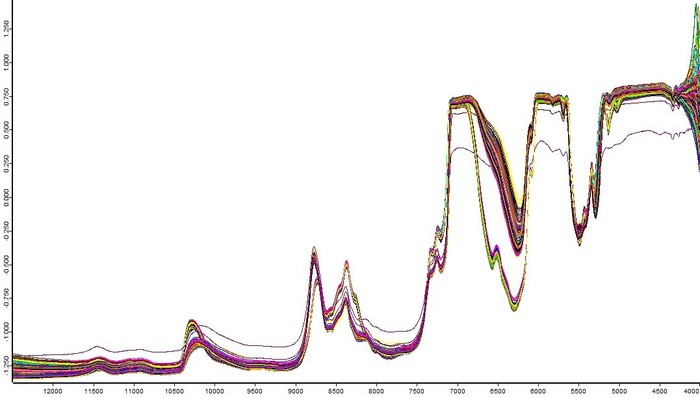
Figure 1. Original NIR spectrum taken with FT-NIR spectrometer. The figure shows the non-preprocessed spectral dataset collected over a period of time by the FT-NIR spectrometer. Please click here to view a larger version of this figure.

Figure 2. Determination coefficient for the o-cresol concentration determined by PLSR. The figure shows the trend of the determination coefficient for the o-cresol concentration with increasing number of components. Please click here to view a larger version of this figure.

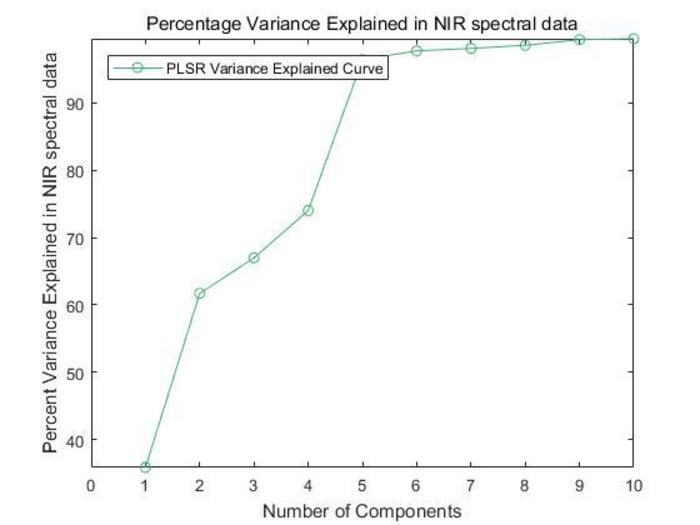
Figure 3. Percent variance explained in the NIR spectral data for the PLSR. The figure shows the percent variance explained in the NIR spectral data for the principal components under the PLSR. Please click here to view a larger version of this figure.

Figure 4. Residual of the PLSR for the test set. The figure shows the residuals of the 200 test set samples for the PLSR. Please click here to view a larger version of this figure.

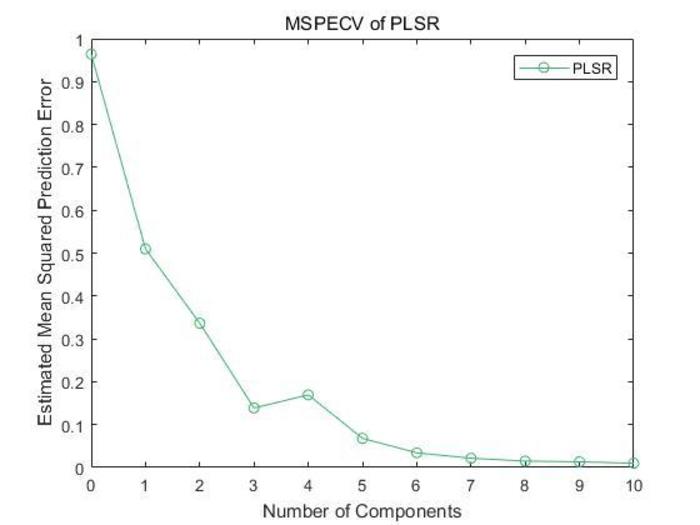
Figure 5. MSPECV of the PLSR. The precision of the PLSR model was evaluated with a 10-fold cross-validation; the MSPECV of model is shown in Figure 5. Please click here to view a larger version of this figure.

	Interpretability	Prediction accuracy
PLSR	R²	R_p	MRPECV
PLSR	0.98332	0.9916	0.01106

Table 1. Evaluation indices of the model. Table 1 shows the model evaluation indicators for a 10-fold cross-validation.

Discussion

This protocol describes the process of performing the PLSR on the measurement of the o-cresol concentration remaining in the liquid product of polyphenylene ether with NIRS.

The two critical steps in this process are the pre-processing of the original NIR spectral data and the variables selection of the high-dimensional NIR spectral data.

Generally, the non-systematic background interference leads to the non-systematic scattering deviation or baseline drift of NIR spectrum. Proper NIR spectral pre-processing method (derivative, normalization, multivariate scattering correction, etc.), as the first critical step, eliminates background interference and increases the signal-to-noise ratio of data.

Multiple linear correlations existing in the high-dimensional NIR spectral data introduces unnecessary computation and reduces the operation efficiency of the regression model. Moreover, there are redundant variables that have weak or even no correlation to the o-cresol content in liquid polyphenyl ether products. The variable selection based on PLS, as the second critical step, solves the above two problems, which reduces the complexity of the model and enhances its robustness compared with the direct use of OLSR for modeling.

In addition, the technology has its limitations as following. Firstly, it requires that there is no significant nonlinear correlation between the various dimensional variables of the NIR spectral data. As the PLS algorithm mechanism is based on the expectation of maximizing the variance of NIR spectral data variables and maximizing the Pearson correlation between the selected principal component and the content of o-cresol. Therefore, the operation of the algorithm on data is essentially a linear combination of high-dimensional variables, which does not include the possible nonlinear relationship between data¹⁵. Secondly, due to the offline modeling, it cannot be self-updated. Our work has not yet covered the effects of interaction between o-cresol and solvent molecules or other impurity molecules on NIRS. The interaction between o-cresol and solvents or other impurity molecules may have an unexpected effect on NIRS, but we still have not found an appropriate method to quantify this effect. Thirdly, the change of environment, working condition and other factors may lead to the concept drift of the model.

However, for the existing methods such as physical or chemical separation analysis for the measurement of chemical substance content in the chemical material industry, NIRS detects composition and structural information about chemical substance content from a microscopic molecular perspective. In general, the qualitative transition at the macroscopic level is caused by the quantitative change at the microscopic level. Therefore, this technology has stronger accuracy, timeliness and sensitivity than other methods. Moreover, the combination with data analysis technology can effectively utilize industrial big data, which is conducive to industrial automation and even intelligent construction.

In the future, this technology can be flexibly applied to online measurement of various liquid or solid phase chemicals content in other fine process industries where the measurement of general sensors and laboratory measurement is difficult or unable to meet the industrial requirements¹⁶. Moreover, this technology can be widely combined with advanced control technology due to the real-time feedback of analysis variables and thus meet higher industrial requirements¹⁷^,¹⁸^,¹⁹.

Disclosures

The authors have nothing to disclose.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 61722306 and 61473137) and National First-class Discipline Program of Light Industry Technology and Engineering (LITE2018-025).

Materials

MPA II Multi Purpose FT-NIR Analyzer	Bruker	1
Fiber Optic Probes(Liquid phase)	Bruker	1
Liquid chromatography analyzer	/	1
Laboratory Equipment and Supplies(e.g. test tube, etc.)	/
MATLAB	MathWork	1
OPUS	Bruker	1
Principal computer	DELL	1
The Unscrambler	CAMO	1

References

Nicolai, B. M., et al. Nondestructive measurement of fruit and vegetable quality by means of NIR spectroscopy: A review. Postharvest Biology and Technology. 46 (2), 99-118 (2007).
Chang, C. W., Laird, D. A., Mausbach, M. J., Hurburgh, C. R. Near-infrared reflectance spectroscopy-principal components regression analyses of soil properties. Soil Science Society of America Journal. 65 (2), 480-490 (2001).
Chen, Y., et al. Near-infrared spectroscopy for rapid evaluation of different processing products of Sophora japonica. L. Spectroscopy Letters. 51 (1), 37-44 (2018).
Cayuela, J. A., Garcia, J. F. Nondestructive measurement of squalene in olive oil by near infrared spectroscopy. LWT-FOOD SCIENCE AND TECHNOLOGY. 88, 103-108 (2018).
Joaquim, M., Rudnick, R. L., Shubkin, R. L. Polyphenyl Ether Lubricants. Synthetic Lubricants and High-performance Functional. , 239 (1999).
Grabowska, H., Kaczmarczyk, W., Wrzyszcz, J. Synthesis of 2,6-Xylenol by Alkylation of Phenol with Methanol. Applied Catalysis. 47 (2), 351-355 (1989).
Jeon, D. B., et al. Determination of volatile organic compounds, catechins, caffeine and theanine in Jukro tea at three growth stages by chromatographic and spectrometric methods. FOOD CHEMISTRY. 219, 443-452 (2016).
Davidyuk, E. I., Demchenko, V. F., Klisenko, M. A. Rapid group separation and identification of chlorinated organic compounds by high performance liquid chromatography. JOURNAL OF ANALYTICAL CHEMISTRY. 52 (11), 1058-1065 (1997).
Rinnan, A., Berg, F., Engelsen, S. B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends in Analytical Chemistry. 28 (10), 1201-1222 (2009).
Zou, X. B., Zhao, J. W., Povey, M. J. W., Holmes, M., Mao, H. P. Variables selection methods in near-infrared spectroscopy. Analytica Chimica Acta. (1-2), 14-32 (2010).
Dunn, B. W., Beecher, H. G., Batten, G. D., Ciavarella, S. The potential of near-infrared reflectance spectroscopy for soil analysis – a case study from the Riverine Plain of south-eastern Australia. Australian Journal of Experimental Agriculture. 42 (5), 607-614 (2002).
Wang, C. K., Zhang, T. L., Pan, X. Z. Potential of visible and near-infrared reflectance spectroscopy for the determination of rare earth elements in soil. Geoderma. 306, 120-126 (2017).
Gatius, F., Miralbes, C., David, C., Puy, J. Comparison of CCA and PLS to explore and model NIR data. Chemometrics and Intelligent Laboratory Systems. , 76-82 (2017).
Wold, S., Sjostrom, M., Eriksson, L. PLS-regression: a basic tool of chemometrics. Chemometrics & Intelligent Laboratory. 58 (2), 109-130 (2001).
Douglas, R. K., Nawar, S., Alamar, M. C., Mouazen, A. M., Coulon, F. Rapid prediction of total petroleum hydrocarbons concentration in contaminated soil using vis-NIR spectroscopy and regression techniques. SCIENCE OF THE TOTAL ENVIRONMENT. 616, 147-155 (2017).
Grassi, S., Alamprese, C. Advances in NIR spectroscopy applied to process analytical technology in food industries. CURRENT OPINION IN FOOD SCIENCE. 22 (SI), 17-21 (2018).
Trung, T., Downes, G., Meder, R., Allison, B. Pulp mill and chemical recovery control with advanced analysers – from trees to final product. APPITA. 68 (1), 39-46 (2015).
Vann, L., Sheppard, J. Use of near-infrared spectroscopy (NIRs) in the biopharmaceutical industry for real-time determination of critical process parameters and integration of advanced feedback control strategies using MIDUS control. Journal of Industrial Microbiology& Biotechnology. 44 (12), 1589-1603 (2017).
Modrono, S., Soldado, A., Martinez-Fernandez, A., de la Roza-Delgado, B. Handheld NIRS sensors for routine compound feed quality control: Real time analysis and field monitoring. TALANTA. 162, 597-603 (2017).

Play Video

PDF

DOI

DOWNLOAD MATERIALS LIST

Cite This Article

Chen, Z., Zheng, N., Luan, X., Liu, F. O-cresol Concentration Online Measurement Based On Near Infrared Spectroscopy Via Partial Least Square Regression. J. Vis. Exp. (153), e59077, doi:10.3791/59077 (2019).

Automatically Generated