Hamiltonianos excitónicos para calcular espectros de absorción óptica y propiedades optoelectrónicas de agregados y sólidos moleculares
Summary
Aquí, presentamos un protocolo para parametrizar un Hamiltoniano excitónico de fijación apretada para calcular espectros de absorción óptica y propiedades optoelectrónicas de materiales moleculares a partir de cálculos químicos cuánticos de primeros principios.
Abstract
El diseño racional de agregados moleculares desordenados y sólidos para aplicaciones optoelectrónicas se basa en nuestra capacidad para predecir las propiedades de dichos materiales utilizando métodos teóricos y computacionales. Sin embargo, los grandes sistemas moleculares donde el trastorno es demasiado significativo para ser considerado en el límite perturbativo no pueden describirse utilizando la primera química cuántica de principios o la teoría de la banda. El modelado multiescala es un enfoque prometedor para comprender y optimizar las propiedades optoelectrónicas de estos sistemas. Utiliza métodos químicos cuánticos de primeros principios para calcular las propiedades de moléculas individuales, luego construye modelos Hamiltonianos de agregados moleculares o materiales a granel basados en estos cálculos. En este artículo, presentamos un protocolo para la construcción de un Hamiltoniano de fijación ajustada que representa los estados excitados de un material molecular en la base de Frenckel excitons: pares de electrones-agujero que se localizan en moléculas individuales que componen el material. La parametrización hamiltoniana propuesta aquí explica los acoplamientos excitónicos entre moléculas, así como la polarización electrostática de la densidad de electrones en una molécula por la distribución de carga en las moléculas circundantes. Este modelo Hamiltonianos se puede utilizar para calcular espectros de absorción óptica y otras propiedades optoelectrónicas de agregados moleculares y sólidos.
Introduction
En las últimas dos décadas, sólidos y películas que están hechas de moléculas orgánicas agregadas han encontrado múltiples aplicaciones en dispositivos optoelectrónicos. Los dispositivos basados en estos materiales tienen muchas propiedades atractivas, incluyendo peso pequeño, flexibilidad, bajo consumo de energía y potencial de producción barata utilizando la impresión de inyección de tinta. Las pantallas basadas en diodos orgánicos emisores de luz (OLED) están reemplazando las pantallas cristalinas líquidas como estado de la técnica para teléfonos móviles, portátiles, televisores y otros dispositivos electrónicos1,2,3,4. Se espera que la importancia de los ODOpara las aplicaciones de iluminación aumente en los próximos años4. El rendimiento de los dispositivos fotovoltaicos orgánicos está mejorando constantemente, con eficiencias de conversión de energía por encima del 16% recientemente reportadas para células solares orgánicas de unión única5. Los materiales orgánicos también tienen el potencial de interrumpir otras tecnologías, como las comunicaciones de fibra óptica, donde su uso permite el desarrollo de moduladores electroópticos con anchos de banda extremadamente altos de 15 THz y superioresa6,7.
Un desafío importante en la optimización de materiales moleculares de estado sólido para aplicaciones en optoelectrónica es que normalmente sus propiedades dependen en gran medida de la estructura a nanoescala del material. El proceso de producción permite definir la nanoestructura de un material en cierta medida mediante el uso de técnicas de crecimiento controlado, tales como la deposición de vapor químico,8 plantillas de moléculas ópticamente activas en otro material (es decir, una matriz depolímeros 9,10), recocido térmico11,,12,etc. Sin embargo, el trastorno a nanoescala es intrínseco a la mayoría de los materiales moleculares y por lo general no se puede eliminar por completo. Por lo tanto, entender cómo el trastorno afecta las propiedades de un material y encontrar maneras de diseñarlo para un rendimiento óptimo es esencial para el diseño racional de materiales optoelectrónicos orgánicos.
El grado de trastorno en los materiales moleculares suele ser demasiado grande para tratarlo como una perturbación de una estructura cristalina periódica con una estructura electrónica que puede ser descrita por la teoría de la banda. Por otro lado, el número de moléculas que deben incluirse en una simulación para reproducir las propiedades de un material a granel o una película es demasiado grande para utilizar los primeros principios métodos químicos cuánticos como la teoría funcional de densidad (DFT)13,14 y la teoría funcional de densidad dependiente del tiempo (TD-DFT)15,16. Las moléculas orgánicas con aplicaciones en optoelectrónica suelen tener sistemas relativamente grandes conjugados; muchos también tienen grupos de donantes y aceptadores. Capturar el comportamiento correcto de transferencia de carga en estas moléculas es esencial para calcular sus propiedades optoelectrónicas, pero sólo se puede lograr utilizando funciones híbridas corregidas de largo alcance en TD-DFT17,,18,,19,,20. Los cálculos que utilizan tales funciones se escalan súper linealmente con el tamaño del sistema y, en la actualidad, sólo son prácticos para modelar las propiedades optoelectrónicas de moléculas orgánicas individuales o pequeños agregados moleculares que se pueden describir utilizando no más de 104 funciones de base atómica. Un método de simulación que podría describir materiales desordenados que consisten en un gran número de cromóforos sería muy útil para modelar estos sistemas.
La magnitud de las interacciones intermoleculares en los materiales moleculares es a menudo comparable o menor que el orden de variación en los parámetros energéticos (como las energías eigenestatales o las energías de excitación) entre moléculas individuales que componen el material. En tales casos, el modelado multiescala es el enfoque más prometedor para comprender y optimizar las propiedades optoelectrónicas de los grandes sistemas moleculares desordenados21,,22,,23. Este enfoque utiliza métodos químicos cuánticos de primeros principios (normalmente DFT y TD-DFT) para calcular con precisión las propiedades de las moléculas individuales que componen el material. El Hamiltoniano de una muestra de material que es lo suficientemente grande como para representar el material molecular a granel (tal vez, mediante el empleo de condiciones límite periódicas) se construye utilizando los parámetros que se calcularon para moléculas individuales. Este Hamiltoniano se puede utilizar para calcular los parámetros optoelectrónicos de un agregado molecular grande, una película delgada o un material molecular a granel.
Los modelos exciton son una subclase de modelos multiescala en los que los estados excitados de un material molecular se representan en base a exciminutos:pares de electrones-agujeros que están unidos por la atracción Coulomb24,25. Para modelar muchos procesos de estado excitado, es suficiente incluir sólo excitons de Frenkel26,donde el electrón y el agujero se localizan en la misma molécula. Los excicranos de transferencia de carga, donde el electrón y el agujero están localizados en diferentes moléculas, pueden necesitar ser incluidos en algunos casos (por ejemplo, al modelar la separación de carga en sistemas de donante-aceptador)27,28. Aunque los modelos de excitón son modelos multiescala que se pueden parametrizar utilizando sólo cálculos de primer principio en moléculas individuales, todavía tienen en cuenta las interacciones intermoleculares. Los dos tipos de interacción principales que pueden explicar son (a) acoplamientos excitónicos entre moléculas que caracterizan la capacidad de los excicidores para deslocalizar o transferir entre moléculas y (b) polarización electrostática de la densidad de electrones en una molécula por la distribución de carga en las moléculas circundantes. Hemos demostrado previamente que ambos factores son importantes para modelar las propiedades ópticas y electroópticas de los agregados moleculares, como los espectros de absorción óptica29 y las primeras hiperpolarizabilidades30.
En este artículo, presentamos un protocolo para parametrizar modelos de exciton que se pueden utilizar para calcular los espectros ópticos y otras propiedades optoelectrónicas de grandes agregados moleculares y materiales moleculares a granel. Se supone que el Hamiltoniano excitónico es un Hamiltoniano de24,,25,
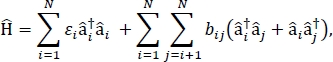
donde i es la energía de excitación de la molécula ith en el material, bij es el acoplamiento excitónico entre las moléculas ith y jth, i y i son los operadores de creación y aniquilación, respectivamente, para un estado excitado en la molécula ith en el material. i† Los parámetros hamiltonianos excitónicos se encuentran utilizando cálculos TD-DFT que se realizan en moléculas individuales que componen el material. En estos cálculos TD-DFT, la distribución de la carga en todas las demás moléculas del material está representada por la incrustación electrostática de cargas de punto atómico para tener en cuenta la polarización electrostática de la densidad electrónica de una molécula. Las energías de excitación, i, para moléculas individuales se toman directamente de la salida de cálculo TD-DFT. Los acoplamientos excónicos, bij, entre moléculas se calculan utilizando el método de cubo de densidad de transición31,con las densidades de transición de estado de tierra a excitación para las moléculas que interactúan tomadas de la salida de un cálculo TD-DFT en Gaussian32 y posteriores al procesamiento utilizando el analizador multifunción de onda33. Multiwfn Para simular las propiedades de los sólidos moleculares a granel, se pueden aplicar condiciones límite periódicas al Hamiltoniano.
El protocolo actual requiere que el usuario tenga acceso a los programas Gaussian32 y Multiwfn33. El protocolo ha sido probado usando Gaussian 16, revisión B1 y Multiwfn versión 3.3.8, pero también debería funcionar para otras versiones recientes de estos programas. Además, el protocolo utiliza una utilidad C++ personalizada y una serie de scripts personalizados de Python 2.7 y Bash, cuyo código fuente se proporciona bajo la Licencia Pública General GNU (Versión 3) en https://github.com/kocherzhenko/ExcitonicHamiltonian. Los cálculos están diseñados para realizarse en una máquina que ejecuta un sistema operativo de la familia Unix/Linux.
Protocol
Representative Results
Discussion
El método que se presenta aquí permite múltiples personalizaciones. Por ejemplo, es posible modificar los parámetros de los cálculos DFT y TD-DFT, incluyendo la densidad funcional, el conjunto de bases y la definición específica de las cargas de punto atómico.
Se recomienda utilizar funciones de largo alcance corregidas, como por ejemplo, b97X, B97XD o PBE, con el fin de obtener densidades de transición razonables para transiciones con carácter de transferencia de carga. Puede ser in…
Disclosures
The authors have nothing to disclose.
Acknowledgements
Agradecemos al Dr. Andreas Tillack (Laboratorio Nacional Oak Ridge), al Dr. Lewis Johnson (Universidad de Washington) y al Dr. Bruce Robinson (Universidad de Washington) por desarrollar el programa de simulaciones de Monte Carlo de grano grueso que se utilizó para generar la estructura del sistema molecular presentado en la sección de Resultados Representativos. A.A.K. y P.F.G. cuentan con el apoyo de un premio de investigación colaborativa de la Facultad de Ciencias de la CSU East Bay. M.H. cuenta con el apoyo de una beca Forever Pioneer del Center for Student Research, CSU East Bay. C.M.I. y S.S. cuentan con el apoyo del Departamento de Defensa de los Estados Unidos (Propuesta 67310-CH-REP) bajo la División de Materiales Orgánicos de investigación científica de la Fuerza Aérea.
Materials
| Gaussian 16, revision B1 |
| Multiwfn version 3.3.8 |
| GNU compiler collection version 9.2 |
| python 2.7.0 |
References
- Tsujimura, T. . OLED Display Fundamentals and Applications, 2nd Ed. , (2017).
- Barnes, D. LCD or OLED: Who Wins. SID Symposium Digest of Technical Papers. 44 (1), 26-27 (2013).
- Mizukami, M., et al. Flexible Organic Light-Emitting Diode Displays Driven by Inkjet-Printed High-Mobility Organic Thin-Film Transistors. IEEE Electron Device Letters. 39 (1), 39-42 (2018).
- Koden, M. . OLED Displays and Lighting. , (2017).
- Fan, B., et al. Achieving Over 16% Efficiency for Single-Junction Organic Solar Cells. Science China Chemistry. 62 (6), 746-752 (2018).
- Dalton, L. R., Gunter, P., Jazbinsek, M., Kwon, O. P., Sullivan, P. A. . Organic Electro-Optics and Photonics: Molecules, Polymers, and Crystals. , (2015).
- Robinson, B. H., et al. Optimization of Plasmonic-Organic Hybrid Electro-Optics. Journal of Lightwave Technology. 36 (21), 5036-5047 (2018).
- Yu, D., Yang, Y. Q., Chen, Z., Tao, Y., Liu, Y. F. Recent Progress on Thin-Film Encapsulation Technologies for Organic Electronic Devices. Optics Communications. 362 (1), 43-49 (2016).
- Wanapun, D., Hall, V. J., Begue, N. J., Grote, J. G., Simpson, G. J. DNA-Based Polymers as Chiral Templates for Second-Order Nonlinear Optical Materials. ChemPhysChem. 10 (15), 2674-2678 (2009).
- Siao, Y. Y., et al. Orderly Arranged NLO Materials on Exfoliated Layered Templates Based on Dendrons with Alternating Moieties at the Periphery. Polymer Chemistry. 4 (9), 2747-2759 (2013).
- Sepeai, S., Salleh, M. M., Yahaya, M., Umar, A. A. Improvement of White Organic Light Emitting Diode Performances by an Annealing Process. Thin Solid Films. 517 (16), 4679-4683 (2009).
- Mao, G., et al. Considerable Improvement in the Stability of Solution Processed Small Molecule OLED by Annealing. Applied Surface Science. 257 (17), 7394-7398 (2011).
- Parr, R. G., Yang, W. . Density Functional Theory of Atoms and Molecules. , (1989).
- Dreizlerm, R. M., Gross, E. K. U. . Density Functional Theory: An Approach to the Quantum Many-body Problem. , (1990).
- Burke, K., Werschnik, J., Gross, E. K. U. Time-Dependent Density Functional Theory: Past, Present, and Future. Journal of Chemical Physics. 123 (6), 062206 (2005).
- Ullrich, C. . Time-Dependent Density-Functional Theory: Concepts and Applications. , (2011).
- Vydrov, O. A., Scuseria, G. E. Assessment of a Long-Range Corrected Hybrid Functional. Journal of Chemical Physics. 125 (23), 234109 (2006).
- Tawada, Y., Tsuneda, T., Yanagisawa, S. A Long-Range-Corrected Time-Dependent Density Functional Theory. Journal of Chemical Physics. 120 (18), 5425 (2004).
- Rohrdanz, M. A., Herbert, J. M. Simultaneous Benchmarking of Ground- and Excited-State Properties with Long-Range-Corrected Density Functional Theory. Journal of Chemical Physics. 129 (3), 034107 (2008).
- Autschbach, J. Charge-Transfer Excitations and Time-Dependent Density Functional Theory: Problems and Some Proposed Solutions. ChemPhysChem. 10 (11), 1757-1760 (2008).
- Nelson, J., Kwiatkowski, J. J., Kirkpatrick, J., Frost, J. M. Modeling Charge Transport in Organic Photovoltaic Materials. Accounts of Chemical Research. 42 (11), 1768-1778 (2009).
- Walker, A. B. Multiscale Modeling of Charge and Energy Transport in Organic Light-Emitting Diodes and Photovoltaics. Proceedings of the IEEE. 97 (9), 1587-1596 (2009).
- Wang, L., Li, Q., Shuai, Z., Chenc, L., Shic, Q. Multiscale Study of Charge Mobility of Organic Semiconductor with Dynamic Disorders. Physical Chemistry Chemical Physics. 12 (13), 3309-3314 (2010).
- Davydov, A. S. . Theory of Molecular Excitons. , (1971).
- Agranovich, V. M. Excitations in Organic Solids. International Series of Monographs on Physics. 142, (2008).
- Frenkel, J. On the Transformation of Light into Heat in Solids. I. Physical Review. 37 (1), 17-44 (1931).
- Kocherzhenko, A. A., Lee, D., Forsuelo, M. A., Whaley, K. B. Coherent and Incoherent Contributions to Charge Separation in Multichromophore Systems. Journal of Physical Chemistry C. 119 (14), 7590-7603 (2015).
- Lee, D., Forsuelo, M. A., Kocherzhenko, A. A., Whaley, K. B. Higher-Energy Charge Transfer States Facilitate Charge Separation in Donor-Acceptor Molecular Dyads. Journal of Physical Chemistry C. 121 (24), 13043-13051 (2017).
- Kocherzhenko, A. A., Sosa Vazquez, X. A., Milanese, J. M., Isborn, C. M. Absorption Spectra for Disordered Aggregates of Chromophores Using the Exciton Model. Journal of Chemical Theory and Computation. 13 (8), 3787-3801 (2017).
- Kocherzhenko, A. A., et al. Unraveling Excitonic Effects for the First Hyperpolarizabilities of Chromophore Aggregates. Journal of Physical Chemistry C. 123 (22), 13818-13836 (2019).
- Krueger, B., Scholes, G., Fleming, G. Calculation of Couplings and Energy-Transfer Pathways between the Pigments of LH2 by the ab Initio Transition Density Cube Method. Journal of Physical Chemistry B. 102 (27), 5378-5386 (1998).
- Frisch, M. J., et al. Gaussian 16, Revision B.01. Gaussian, Inc. , (2016).
- Lu, T., Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. Journal of Computational Chemistry. 33 (5), 580-592 (2012).
- Chai, J. D., Head-Gordon, M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. Journal of Chemical Physics. 128 (8), 084106 (2008).
- Hehre, W., Ditchfield, R., Pople, J. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. Journal of Chemical Physics. 56 (5), 2257-2261 (1972).
- Hariharan, P., Pople, J. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theoretica chimica acta. 28 (3), 213-222 (1973).
- Breneman, C. M., Wiberg, K. B. Determining Atom-Centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis. Journal of Computational Chemistry. 11 (3), 361-373 (1990).
- Mulliken, R. S. Electronic Population Analysis on LCAO-MO MolecularWave Functions. I. Journal of Chemical Physics. 23 (10), 1833-1840 (1955).
- Jen, A., et al. Exceptional Electro-Optic Properties through Molecular Design and Controlled Self-Assembly. Proceedings of SPIE. 5935, 593506 (2005).
- Hirata, S., Head-Gordon, M. Time-Dependent Density Functional Theory Within the Tamm-Dancoff Approximation. Chemical Physics Letters. 314 (3-4), 291-299 (1999).
- Randolph, K. A., Myers, L. L. . Basic Statistics in Multivariate Analysis. , 11-34 (2013).
- Garrett, K., et al. Optimum Exchange for Calculation of Excitation Energies and Hyperpolarizabilities of Organic Electro-optic Chromophores. Journal of Chemical Theory and Computation. 10 (9), 3821-3831 (2014).
- Sekino, H., Maeda, Y. Polarizability and Second Hyperpolarizability Evaluation of Long Molecules by the Density Functional Theory with Long-Range Correction. Journal of Chemical Physics. 126 (1), 014107 (2007).
- Johnson, L. E., Dalton, L. R., Robinson, B. H. Optimizing Calculations of Electronic Excitations and Relative Hyperpolarizabilities of Electrooptic Chromophores. Accounts of Chemical Research. 47 (11), 3258-3265 (2014).
- Lee, J., et al. Molecular Mechanics Simulations and Improved Tight-Binding Hamiltonians for Artificial Light Harvesting Systems: Predicting Geometric Distributions, Disorder, and Spectroscopy of Chromophores in a Protein Environment. Journal of Physical Chemistry B. 122 (51), 12292-12301 (2018).
- Bellinger, D., Pflaum, J., Brüning, C., Engel, V., Engels, B. The Electronic Character of PTCDA Thin Films in Comparison to Other Perylene-Based Organic Semi-conductors: Ab Initio-, TD-DFT and Semi-Empirical Computations of the Opto-Electronic Properties of Large Aggregates. Physical Chemistry Chemical Physics. 19 (3), 2434 (2017).
- Zuehlsdorff, T. J., Isborn, C. M. Combining the Ensemble and Franck-Condon Approaches for Calculating Spectral Shapes of Molecules in Solution. The Journal of Chemical Physics. 148 (2), 024110 (2018).
- Zuehlsdorff, T. J., Isborn, C. M. Modeling Absorption Spectra of Molecules in Solution. International Journal of Quantum Chemistry. 119 (1), 25719 (2019).
- Plötz, P. A., Megow, J., Niehaus, T., Kühn, O. All-DFTB Approach to the Parametrization of the System-Bath Hamiltonian Describing Exciton-Vibrational Dynamics of Molecular Assemblies. Journal of Chemical Theory and Computation. 14 (10), 5001-5010 (2018).
- Tillack, A., Johnson, L., Eichinger, B., Robinson, B. H. Systematic Generation of Anisotropic Coarse-Grained Lennard-Jones Potentials and Their Application to Ordered Soft Matter. Journal of Chemical Theory and Computation. 12 (9), 4362-4374 (2016).

