Excitonic Hamiltonians for Calculating Optical Absorption Spectra and Optoelectronic Properties of Molecular Aggregates and Solids

Aleksey A. Kocherzhenko; Sapana  V. Shedge; Pauline  F. Germaux; Mohammad Heidarian; Christine  M. Isborn

doi:10.3791/60598

JoVE Journal > Chemistry

Chemie

Excitonic Hamiltonians for Calculating Optical Absorption Spectra and Optoelectronic Properties of Molecular Aggregates and Solids

Published: May 27, 2020

doi:

10.3791/60598

Aleksey A. Kocherzhenko¹, Sapana V. Shedge², Pauline F. Germaux¹, Mohammad Heidarian¹, Christine M. Isborn²

¹Department of Chemistry and Biochemistry,California State University, East Bay, ²Department of Chemistry and Chemical Biology,University of California, Merced

Summary

Here, we present a protocol for parametrizing a tight-binding excitonic Hamiltonian for calculating optical absorption spectra and optoelectronic properties of molecular materials from first-principles quantum chemical calculations.

Abstract

Rational design of disordered molecular aggregates and solids for optoelectronic applications relies on our ability to predict the properties of such materials using theoretical and computational methods. However, large molecular systems where disorder is too significant to be considered in the perturbative limit cannot be described using either first principles quantum chemistry or band theory. Multiscale modeling is a promising approach to understanding and optimizing the optoelectronic properties of such systems. It uses first-principles quantum chemical methods to calculate the properties of individual molecules, then constructs model Hamiltonians of molecular aggregates or bulk materials based on these calculations. In this paper, we present a protocol for constructing a tight-binding Hamiltonian that represents the excited states of a molecular material in the basis of Frenckel excitons: electron-hole pairs that are localized on individual molecules that make up the material. The Hamiltonian parametrization proposed here accounts for excitonic couplings between molecules, as well as for electrostatic polarization of the electron density on a molecule by the charge distribution on surrounding molecules. Such model Hamiltonians can be used to calculate optical absorption spectra and other optoelectronic properties of molecular aggregates and solids.

Introduction

In the past two decades, solids and films that are made from aggregated organic molecules have found multiple applications in optoelectronic devices. Devices based on such materials have many attractive properties, including small weight, flexibility, low power consumption, and potential for cheap production using inkjet printing. Displays based on organic light emitting diodes (OLEDs) are replacing liquid crystalline displays as state of the art for mobile phones, laptops, television sets, and other electronic devices¹^,²^,³^,⁴. The importance of OLEDs for lighting applications is expected to increase in the coming years⁴. The performance of organic photovoltaic devices is steadily improving, with power conversion efficiencies above 16% recently reported for single-junction organic solar cells⁵. Organic materials also have the potential to disrupt other technologies, such as fiber-optic communications, where their use enables the development of electro-optic modulators with extremely high bandwidths of 15 THz and above⁶^,⁷.

A major challenge in optimizing solid-state molecular materials for applications in optoelectronics is that typically their properties strongly depend on the nanoscale structure of the material. The production process allows defining the nanostructure of a material to some extent by using controlled growth techniques, such as chemical vapor deposition,⁸ templating of optically active molecules onto another material (i.e., a polymer matrix⁹^,¹⁰), thermal annealing¹¹^,¹², etc. However, nanoscale disorder is intrinsic to most molecular materials and usually cannot be eliminated entirely. Therefore, understanding how disorder affects the properties of a material and finding ways to engineer it for optimal performance is essential for the rational design of organic optoelectronic materials.

The degree of disorder in molecular materials is usually too great to treat it as a perturbation of a periodic crystalline structure with an electronic structure that can be described by band theory. On the other hand, the number of molecules that must be included in a simulation to reproduce the properties of a bulk material or a film is too great to use first principles quantum chemical methods like density functional theory (DFT)¹³^,¹⁴ and time-dependent density functional theory (TD-DFT)¹⁵^,¹⁶. Organic molecules with applications in optoelectronics typically have relatively large π-conjugated systems; many also have donor and acceptor groups. Capturing the correct charge-transfer behavior in such molecules is essential to calculating their optoelectronic properties, but it can only be accomplished using long-range corrected hybrid functionals in TD-DFT¹⁷^,¹⁸^,¹⁹^,²⁰. Calculations that use such functionals scale super linearly with the size of the system and, at present, they are only practical for modeling the optoelectronic properties of individual organic molecules or small molecular aggregates that can be described using no more than ~10⁴ atomic basis functions. A simulation method that could describe disordered materials that consist of large numbers of chromophores would be very useful for modeling these systems.

The magnitude of intermolecular interactions in molecular materials is often comparable to or smaller than the order of variation in the energetic parameters (such as the eigenstate energies or excitation energies) between individual molecules that make up the material. In such cases, multiscale modeling is the most promising approach to understanding and optimizing the optoelectronic properties of large disordered molecular systems²¹^,²²^,²³. This approach uses first-principles quantum chemical methods (usually DFT and TD-DFT) to accurately calculate the properties of individual molecules that compose the material. The Hamiltonian of a material sample that is large enough to represent the bulk molecular material (perhaps, by employing periodic boundary conditions) is then constructed using the parameters that were calculated for individual molecules. This Hamiltonian can then be used to calculate the optoelectronic parameters of a large molecular aggregate, a thin film, or a bulk molecular material.

Exciton models are a subclass of multiscale models in which excited states of a molecular material are represented in a basis of excitons: electron-hole pairs that are bound by Coulomb attraction²⁴^,²⁵. For modeling many excited state processes, it is sufficient to only include Frenkel excitons²⁶, where the electron and the hole are localized on the same molecule. Charge transfer excitons, where the electron and the hole are localized on different molecules, may need to be included in some cases (e.g., when modeling charge separation in donor-acceptor systems)²⁷^,²⁸. Although exciton models are multiscale models that can be parametrized using only first-principle calculations on individual molecules, they still account for intermolecular interactions. The two primary interaction types that they can account for are (a) excitonic couplings between molecules that characterize the ability of excitons to delocalize across or transfer between molecules and (b) electrostatic polarization of the electron density on a molecule by the charge distribution on surrounding molecules. We have previously shown that both of these factors are important for modeling the optical and electro-optic properties of molecular aggregates, such as the optical absorption spectra²⁹ and first hyperpolarizabilities³⁰.

In this paper, we present a protocol for parametrizing exciton models that can be used to calculate the optical spectra and other optoelectronic properties of large molecular aggregates and bulk molecular materials. The excitonic Hamiltonian is assumed to be a tight-binding Hamiltonian²⁴^,²⁵,

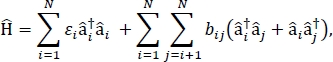
where ε_i is the excitation energy of the i^th molecule in the material, b_ij is the excitonic coupling between the i^th and the j^th molecules, â_i^† and â_i are the creation and annihilation operators, respectively, for an excited state on the i^th molecule in the material. The excitonic Hamiltonian parameters are found using TD-DFT calculations that are performed on individual molecules that make up the material. In these TD-DFT calculations, the charge distribution on all other molecules in the material is represented by electrostatic embedding of atomic point charges to account for electrostatic polarization of a molecule’s electronic density. The excitation energies, ε_i, for individual molecules are taken directly from the TD-DFT calculation output. The excitonic couplings, b_ij, between molecules are calculated using the transition density cube method³¹, with the ground-to-excited state transition densities for the interacting molecules taken from the output of a TD-DFT calculation in Gaussian³² and post-processed using the Multiwfn multifunctional wavefunction analyzer³³. For simulating the properties of bulk molecular solids, periodic boundary conditions may be applied to the Hamiltonian.

The current protocol requires that the user have access to the Gaussian³² and Multiwfn³³ programs. The protocol has been tested using Gaussian 16, revision B1 and Multiwfn version 3.3.8, but should also work for other recent versions of these programs. In addition, the protocol uses a custom C++ utility and a number of custom python 2.7 and Bash scripts, the source code for which is provided under the GNU General Public License (Version 3) at https://github.com/kocherzhenko/ExcitonicHamiltonian. The calculations are intended to be performed on a machine running an operating system from the Unix/Linux family.

Protocol

1. Splitting the multi-molecular system into individual molecules

Generate the structure of the system for which the excitonic Hamiltonian needs to be constructed in Tripos MOL2 molecular file format. This structure can be a snapshot from a molecular dynamics or Monte Carlo simulation of the system.
If all molecules in the system consist of the same number of atoms, use the python 2.7 script getMonomers.py to generate files that contain the Cartesian coordinates for atoms in individual molecules that compose the system. Molecules that make up the system do not have to be identical (e.g., they can be isomers). This script takes two input parameters.
1. Specify the name of the Tripos MOL2 file that contains the geometry of the system from step 1.1 (a string).
2. Specify the number of atoms in each individual molecule that makes up the system (an integer). To complete this step, use the command:
  ./getMonomers.py YLD124-300K_0-210000.mol2 125
  Takes the structure that is contained in the sample file YLD124-300K_0-210000.mol2 on Github; writes Cartesian coordinates of individual molecules to files monomer_N.com in XYZ format, where N is a four-digit number that identifies the molecule in the system.
If a system consists of molecules with different numbers of atoms, generate the structures for individual molecules using an alternative script or manually. The procedure described in subsequent steps can be used without any modifications.

2. Generating ground state point charges for atoms in individual molecules

Set up a plain text file, chargeOptions.txt, with the options for a Gaussian DFT calculation of the atomic point charges in the ground state of an electrically neutral molecule. In order to obtain a reasonably accurate charge distribution for transitions with charge-transfer character, it is recommended to specify the parameters as follows.
1. Use a long-range corrected density functional (such as ωB97X)³⁴.
2. Use a sufficiently large basis set that includes at least d polarization functions on non-hydrogen atoms (such as 6-31G*)³⁵^,³⁶.
3. Use a superfine integration grid.
4. Use a very tight self-consistent field convergence criterion (energy convergence to 10^–10 Hartree).
5. Use atomic point charges that are fit to reproduce the electrostatic potential in the vicinity of the molecule, as is done in the CHelpG method³⁷, because the calculated atomic charges will be used to represent the electrostatic environment.
  NOTE: In typical molecular aggregates and solids distances between molecules are relatively large, so it is often acceptable to use other atomic point charge definitions, such as Mulliken charges³⁸.
6. Include the NoSymm keyword in the input file to ensure that the atomic coordinates in the Gaussian output file are written in input orientation, rather than in standard orientation.
7. Specify the name of the calculation in the comment line of the Gaussian input file.
8. Specify the charge and multiplicity of the molecule (0 and 1, respectively) in a separate line. Sample calculation options specified in the file chargeOptions.txt may be:
  #p wB97X/6-31G* Integral(Grid=SuperFineGrid) NoSymm SCF(Conver=10) Pop=CHelpG
  Monomer charges
  0 1
Set up the Gaussian input files for all individual molecules that make up the system using the parameters in the file chargeOptions.txt. This step can be efficiently accomplished using the following Bash script:
for f in monomer_*.xyz
do
cat chargeOptions.txt > ${f%xyz}com
tail -n +3 $f >> ${f%xyz}com
echo "" >> ${f%xyz}com
done
NOTE: The script will produce Gaussian input files with the same names as the XYZ files generated in step 1.2, but with the extension .com. These files will contain the calculation options specified in chargeOptions.txt and the atomic coordinates from the respective .xyz files, terminated by a blank line.
Run the Gaussian calculations, specifying the output file name to be the same as the input .com filename, but with the extension .log.
Extract the CHelpG atomic point charges from the Gaussian output files with the extension .log, using the python 2.7 script getCHelpG.py. The script takes 2 input parameters: the name of the Gaussian output file with the extension .log and the number of atoms in a single molecule.
NOTE: The script getCHelpG.py writes a file with the same name as the Gaussian output file, but with the extension .chg. There are 4 columns in this file: the first three with the Cartesian coordinates of atoms in the molecules, the last one with the CHelpG atomic point charges. The following Bash script can efficiently extract charges from all files:
for f in monomer_*.log; do ./getCHelpG.py $f N; done
(N is the number of atoms in a molecule.)
If a definition of the atomic point charges other than CHelpG was used in step 2.1, extract the charges from the Gaussian output file using an alternative script or manually.

3. Calculating the excitation energies and transition densities of individual molecules in the material in the presence of an electrostatic environment

Set up a plain text file, monomerOptions.txt, with the options for a Gaussian TD-DFT calculation of the excited state energies and ground-to-excited state transition density matrices for individual monomers. Suggested parameters are the same as those used for the calculation of the atomic point charges in step 2.1.
1. Use a range-separated density functional, such as ωB97X³⁴.
2. Use a sufficiently large basis set that includes at least d polarization functions on non-hydrogen atoms (such as 6-31G*)³⁵^,³⁶.
3. Use a superfine integration grid.
4. Use a very tight self-consistent field convergence criterion (energy convergence to 10^–10 Hartree).
5. Include the NoSymm keyword to ensure that the atomic coordinates in the Gaussian output file are written in input orientation, rather than in standard orientation;
6. In order to obtain reasonably accurate transition densities, set a low threshold for printing eigenvector components (i.e., even coefficients for basis functions with very small contributions to an eigenvector – ideally, at least to the order of 10^–5 – should be printed to the output file).
  NOTE: To set this condition, one needs to use Gaussian internal options: set overlay 9, option 40 to the absolute value of the exponent for the threshold for printing eigenvector components (e.g., IOp(9/40) = 5 sets the cutoff threshold to 10^–5).
7. Specify the name of the calculation in the comment line of the Gaussian input file.
8. Specify the charge and multiplicity of the molecule (0 and 1, respectively) in a separate line. Sample calculation options specified in the file monomerOptions.txt may be:
  #p tda(NStates=10) wB97X/6-31G* Integral(Grid=SuperFineGrid) NoSymm SCF(Conver=10) iop(9/40=5)
  Monomer with charges
  0 1
Set up the Gaussian input files for the calculation of the excitation energies and transition densities of all individual molecules in the material in the presence of an electrostatic environment represented by the point charges on all other molecules in the material, with file name monomer_N_wCh.com.
1. Include a request to save a Gaussian checkpoint file with filename monomer_N_wCh.chk in the Gaussian input file.
  NOTE: For the naming convention described in this protocol, this step can be accomplished using the python 2.7 script getMonomerWCh.py that reads in the calculation options specified in the file monomerOptions.txt, the atomic coordinates for individual molecules in the system that are stored in files monomer_N.xyz, and atomic point charges for all individual molecules that are stored in files monomer_N.chg (N is the number of the monomer).
Run the Gaussian calculations, specifying the output file name to be the same as the input .com filename, but with the extension .log. The calculation will also save a checkpoint file with the same filename, but with the extension .chk.

4. Extracting excitation energies for bright states of individual molecules that make up the system from the Gaussian output files

Copy the excitation energies for the bright excited states of individual monomers from the Gaussian output files with the extension .log to a plain text file called all_energies.txt.
NOTE: If there is only one bright excited state and all Gaussian output files are in the same directory, then this step can be efficiently accomplished by creating an empty plain text file, all_energies.txt, then appending the line in the output file that contains the excitation energy of the bright state for each monomer using the following Bash script:
for f in monomer*WCh.log; do grep "Excited State M" $f >> all_energies.txt; done
(M is the number of the excited bright state; the number of spaces between the word State and the number M should be the same as in the Gaussian output files.)
In the file all_energies.txt, keep only the column that contains the numerical values of the excitation energies (in eV); delete all other columns.

5. Calculating the excitonic couplings for all pairs of molecules that make up the molecular system

Convert the checkpoint files to human-readable format using the formchk utility that is part of Gaussian using the following Bash script:
for f in monomer_*.chk; do formchk $f; done
NOTE: The human-readable formatted checkpoint files will have the same name as the original checkpoint files, but with the extension .fchk.
Use the python 2.7 script switchSign.py that takes the name of the Gaussian output file with the extension .log and the number of excited states N included in the calculation as input parameters.
NOTE: This script prints out the contents of the .log file switching the direction of the transition dipole moment vectors from the ground to all excited states if the angle between the ground state permanent dipole moment vector and the transition dipole moment vector for the ground to first excited state transition is obtuse.
Save the output produced by the script switchSign.py to a file that has the same name as the .log file, but with the extension .log2.
For molecules where the angle between the ground state permanent dipole moment vector and the transition dipole moment vector for the ground to first excited state transition is acute, copy the .log file to a file with the same name and extension .log2.
NOTE: If the naming convention recommended in this protocol is used, steps 5.2–5.4 can be accomplished efficiently for all individual monomers using the following Bash script:
for f in monomer*_wCh.log
do
./switchSign.py $f 10 > ${f}2
if [ -s ${f}2 ]
then
echo 'Switching transition dipole moment signs for' $f
else
echo 'Copying' $f 'to' ${f}2
cp ${f} ${f}2
fi
done
Use the Multiwfn multifunctional wavefunction analyzer to write the transition density cube file based on the Gaussian formatted checkpoint file with the extension .fchk and the processed Gaussian output file with the extension .log2.
NOTE: Gaussian only natively supports saving the spatial density distribution to a density cube file for observables that correspond to Hermitian operators. Because the transition density operator is not Hermitian, a postprocessing program is required to obtain a density cube file.
1. Launch the Multiwfn program.
2. Submit the Gaussian formatted checkpoint file (the file with the extension .fchk generated in step 5.1) as the input file.
3. Select option 18, Electron excitation analysis, from the Main function menu.
4. Select option 1, Analyze and visualize hole-electron distribution, transition dipole moment and transition density, from the Electron excitation analyses menu.
5. Submit the Gaussian output file with adjusted signs for the transition dipole vectors (the file with the extension .log2 saved in step 5.2) when prompted to Input the path of the Gaussian output file or plain text file containing excitation data.
6. Specify the transition for which the transition density cube file should be generated (if there is only one bright state, it is the transition from the ground state to that state).
7. Select option 1, Visualize and analyze hole, electron and transition density and so on, in the next menu.
8. Select the number of points in the grid for which the transition density cube file will be generated: a larger number of points results in more accurate excitonic couplings, but increases the calculation time significantly, in most cases, option 1, Low quality grid, covering whole system, about 125000 points in total, is sufficient.
9. Select option 13, Output cube file of transition density to current folder, in the following menu. Transition density cube file transdens.cub will be written, rename this file to have the same name as the .log2 and .fchk files, with the extension .cub.
  NOTE: Multiwfn is intended to run interactively, with calculation options entered from the keyboard in response to prompts. However, it is more convenient to set up a file with processing options and then to have Multiwfn read them from that file.
To efficiently generate set up files with Multiwfn processing options for all .fchk files in the current directory, use the Bash script makeOpt.sh. The files written by the script makeOpt.sh have the same names as the .fchk files with the extension .opt.
Generate the transition density cube files in a single batch using the following Bash script:
for f in monomer*_wCh.fchk
do
Multiwfn $f < ${f%fchk}opt
mv transdens.cub ${f%fchk}cub
done
NOTE: Figure 1 shows the transition density for a molecule of 2-[4-[(E,3E)-3-[3-[(E)-2-[4-[bis[2-[tert-butyl-(dimethyl)silyl]oxyethyl]amino]phenyl]ethenyl]-5,5-dimethylcyclohex-2-en-1-ylidene]prop-1-enyl]-3-cyano-5-phenyl-5-(trifluoromethyl)furan-2-ylidene]propanedinitrile (commonly referred to as YLD 124 [Jen2005])³⁹ in the presence of point charges of surrounding molecules.
Convert .cub files to files that explicitly specify the coordinates of the centers of all cubes on the grid used in step 5.5.8 (first 3 columns) and the values of the transition density inside the cube (last column) using the python 2.7 script cubeFormat.py. The script takes the name of a .cub file as input. To convert all .cub files in a directory, use the Bash script:
for f in monomer_0*.cub; do echo $f; ./cubeFormat.py $f; done
NOTE: The script cubeFormat.py writes a formatted density cube file with the same name as the input file it takes, but with the extension .fcub.
Use the .fcub files generated in step 5.8 to calculate the excitonic couplings between all pairs of molecules in the system using the transition density cube method³¹. This step can be accomplished using the cubePairGen program that takes two .fcub files for different molecules as input. To run it, use the command:
./cubePairGen monomer_N_wCh.fcub monomer_M_wCh.fcub
NOTE: The program returns a file named coup_N_M with a single line that contains three numbers: the molecule numbers N and M, followed by the excitonic coupling between these two molecules in eV. The program source code in the file CubePairGen.cpp can be compiled using the C++ compiler in the GNU Compiler Collection with the command:
g++ CubePairGen.cpp –o cubePairGen
If the file naming convention suggested in this protocol is used, the calculations can be run as a batch for all pairs of individual molecules that make up the system studied. To run these calculations, use the following Bash script:
for f in *.fcub
do
for g in *.fcub
do
ff=${f#monomer_}
gg=${g#monomer_}
fff=${ff%_wCh*}
ggg=${gg%_wCh*}
if [ "$fff" -gt "$ggg" ]
then
(*) ./cubePairgen' $f $g '> coup_'${fff}'_'${ggg}
fi
done
done
NOTE: Figure 2 shows the transition densities for two molecules of YLD 124 that are used to calculate the excitonic coupling between these molecules. For large systems, where the total number of molecule pairs is large, the line marked by an asterisk in the Bash script can be modified to submit calculations to a supercomputing cluster’s queuing system.
Once the calculations in step 5.8 are finished, create an empty file all_couplings.txt and combine all excitonic couplings into a single file using the following Bash script:
for f in coup_0*; do cat $f >> all_couplings.txt; done

6. Setting up the excitonic Hamiltonian

Combine the excited state energies in the file all_energies.txt that was generated in step 4.2 and the excitonic couplings in the file all_couplings.txt that was generated in step 5.9 into a single file that contains the complete excitonic Hamiltonian matrix using the python 2.7 script SetupHam.py using the terminal command:
./Setup_Ham.py all_energies.txt all_couplings.txt N >Hamiltonian.txt
NOTE: The program will write a file Hamiltonian.txt with three columns: the row number, column number, and value in eV for each matrix element, with rows separated by blank lines.
1. Specify the name of the file that contains excitonic energies.
2. Specify the name of the file that contains excitonic couplings.
3. Specify the dimension N of the Hamiltonian matrix (the number of molecules in the system).

Representative Results

In this section we present representative results for computing the optical absorption spectrum of an aggregate of six YLD 124 molecules, shown in Figure 3a, where the structure of the aggregate was obtained from a coarse-grained Monte Carlo simulation. YLD 124 is a prototypical charge-transfer chromophore that consists of an electron-donating group of diethyl amine with tert-butyldimethylsilyl protecting groups that is connected via a π -conjugated bridge to the electron accepting group 2-(3-cyano-4,5,5-trimethyl-5H-furan-2-ylidene)-malononitrile³⁹. This molecule has a large ground-state dipole moment, ~30 D. Electronic structure calculations for individual molecules were performed using the ωB97X³⁴ functional with the 6-31G* basis set³⁵^,³⁶. TD-DFT calculations used the Tamm-Dancoff approximation⁴⁰. Partial atomic charges were computed with the CHelpG population analysis method³⁷.

The Hamiltonian for this system, constructed using the protocol described in this paper, is shown in Table 1.

The absorption spectrum calculated for this excitonic Hamiltonian is shown in blue in Figure 3b. Because there are six molecules with only a single bright excited state for each molecule, a 6-by-6 excitonic Hamiltonian was generated, resulting in six transitions. The eigenvalues of this Hamiltonian are the lowest six excited state energies for the molecular aggregate. The height of the vertical lines represents the oscillator strength f_i for each transition from the ground to the i^th excited state of the molecular aggregate. It can be found using the expression²⁹

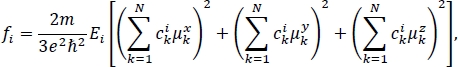
where m is the electron mass, e is the elementary charge, ħ is the reduced Planck’s constant, N is the total number of molecules in the aggregate, E_i is the eigenvalue that corresponds to the i^th excited state of the molecular aggregate, c_kⁱ is the expansion coefficient for the contribution of the k^th molecule in the aggregate to the i^th excited state of the aggregate written in the basis of bright excited states on individual molecules, and μ_k^α are the components of the transition dipole moment vector for the ground to bright excited state of the k^th molecule in the aggregate, α = x, y, z . The values of E_i and c_kⁱ are found by solving the eigenvalue equation for the Hamiltonian matrix (the time-independent Schrödinger equation). The values of μ_k^αcan be found in the “.log2” files that are generated in step 5.2 of the protocol. The total spectrum is a smooth line created by summing over Gaussian functions centered at each of the excitation energies and weighted by the corresponding oscillator strengths²⁹.

For comparison, the spectrum computed from an all-electron TD-DFT calculation on the entire molecular aggregate is shown in magenta. For these spectra, the integrated intensity of the exciton spectrum is larger than the TD-DFT spectrum (I_exc/I_TD-DFT = 1.124) and the difference in the mean absorption energies is E_exc – E_TD-DFT = 0.094 eV. These offsets are systematic for molecular aggregates of a given size and can be corrected for to obtain very good agreement between exciton model and TD-DFT spectra. For instance, for a set of 25 molecular aggregates that each consists of 6 YLD 124 molecules, the average integrated intensity ratio I_exc/I_TD-DFT = 1.126, with a standard deviation of 0.048, and the difference in the mean absorption energies is E_exc – E_TD-DFT = 0.057 eV, with a standard deviation of 0.017 eV. The exciton model and TD-DFT spectra shown in Figure 3b also have similar shapes, as characterized by Pearson’s product-moment correlation coefficient⁴¹ between them of 0.9818 and Pearson’s product-moment correlation coefficient between their derivatives of 0.9315. On average, for a set of 25 molecular aggregates that each consists of 6 YLD 124 molecules, the agreement in spectral shape is even better than for the example shown, with values of 0.9919 (standard deviation of 0.0090) and 0.9577 (standard deviation of 0.0448) for the two Pearson’s coefficients, respectively²⁹. Our earlier work suggests that the spectral shape is primarily determined by local electrostatic interactions between chromophores in the aggregate that are accounted for in the exciton model described in this paper, whereas the excitation energy and intensity depend considerably on the mutual polarization between the chromophore and its environment that the model neglects²⁹.

Figure 1: An isosurface for the transition density plotted for a single molecule of YLD 124. The the positions of atomic charges on surrounding molecules are shown by gray dots. Please click here to view a larger version of this figure.

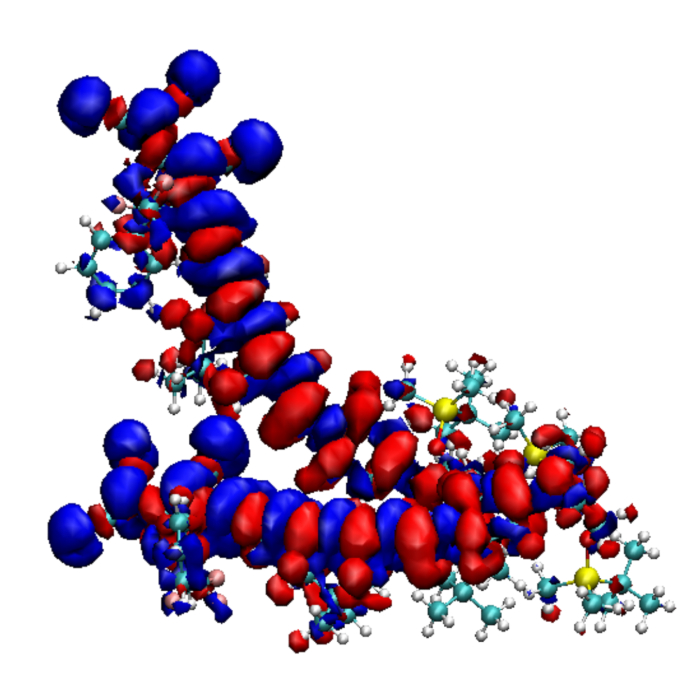
Figure 2: The transition densities plotted for two molecules of YLD 124, i and j, that are used for computing the excitonic coupling b_ij between these molecules. The surrounding charges are not shown. Please click here to view a larger version of this figure.

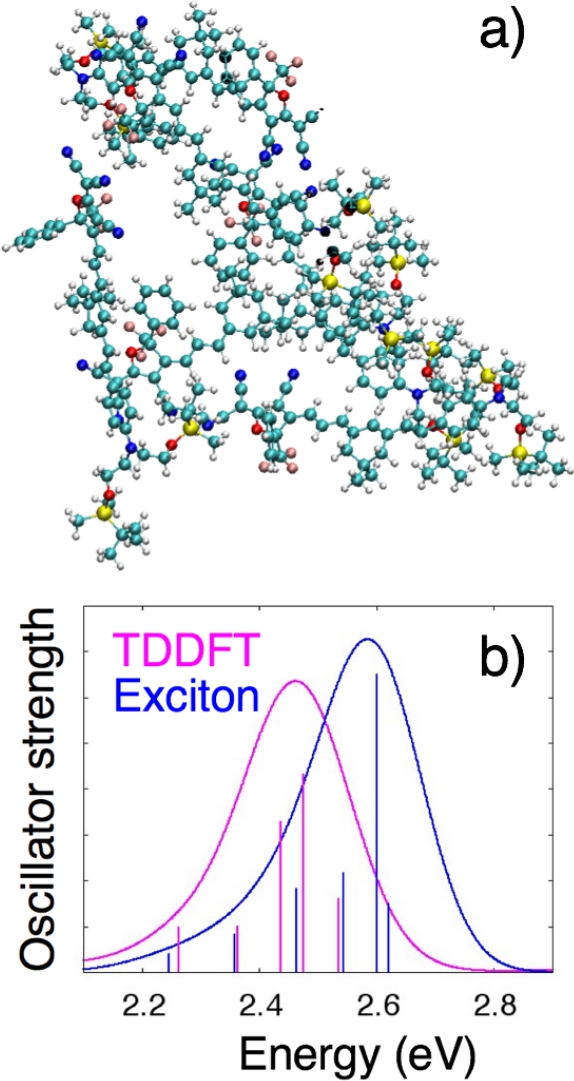
Figure 3: The structure and calculated spectrum for an aggregate of six YLD 124 molecules. (a) The aggregate structure used in the sample calculation. (b) The corresponding absorption spectra created using the exciton model Hamiltonian (blue) and an all-electron TD-DFT calculation on the entire aggregate (magenta). Please click here to view a larger version of this figure.

2.4458	-0.0379	-0.0899	0.0278	-0.0251	0.0120
-0.0379	2.4352	-0.0056	-0.1688	-0.0070	-0.0085
-0.0899	-0.0056	2.5111	0.0032	0.0239	0.0794
0.0278	-0.1688	0.0032	2.3954	0.0057	0.0073
-0.0251	-0.0070	0.0239	0.0057	2.5171	-0.0211
0.0120	-0.0085	0.0794	0.0073	-0.0211	2.5256

Table 1: The Hamiltonian for a sample calculation on the aggregate of six YLD 124 molecules shown in Figure 3a. The diagonal elements are the excitation energies of individual molecules; the off-diagonal elements are the excitonic couplings between molecules (all values are in eV).

Discussion

The method presented here allows for multiple customizations. For instance, it is possible to modify the parameters of the DFT and TD-DFT calculations, including the density functional, basis set, and specific definition of the atomic point charges.

Using long-range corrected functionals, such as ωB97X, ωB97XD, or ωPBE, is recommended in order to obtain reasonable transition densities for transitions with charge-transfer character. It may be interesting to study to what extent the specific choice of functional (or of the functional parameters, such as the amount of exact exchange or the value of the range separation parameter ω) affects the calculated optoelectronic properties for specific systems⁴²^,⁴³^,⁴⁴.

The accuracy of the Hamiltonian parametrization can potentially be improved by using larger basis sets, but at the expense of computational cost. Furthermore, given the approximations intrinsic to the exciton model²⁴^,²⁵, improving its parametrization may not always lead to a significantly improved agreement with experimental observations.

We have found the choice of the specific definition of atomic point charges in the Hamiltonian parametrization to have only a small effect on the resulting optical absorption spectra for aggregates of YLD 124 molecules. It may even be acceptable to use the atomic charges from force fields for roughly representing a molecule’s electrostatic environment. However, using atomic point charges that are computed from first principles for specific molecules in a molecular aggregate for parametrizing the excitonic Hamiltonian leads to improved agreement with absorption spectra calculated using TD-DFT.

Step 5.2 in the protocol is necessary because the transition dipole moment between the ground and excited states of a monomer is not an observable and its phase may be chosen arbitrarily. Gaussian selects this phase so that the components of the transition dipole moment vector are real, but this restriction leaves the signs of the transition dipole moment vector components ambiguous. For calculating the excitonic couplings between monomers, one must ensure that the directions of the transition dipole moment vectors are selected uniformly for all molecules that make up the system. To accomplish this task, one can find the angles between the transition dipole moment vector of each molecule and some vector observable for that molecule (e.g., its permanent ground state dipole moment). If the molecular system is made up of molecules of the same type, even with some geometric variations, the angle between the transition dipole moment and the ground state dipole moment vectors should be relatively similar for all individual molecules. If it turns out that the angle between these vectors is acute for some molecules and obtuse for others, then the direction of the transition dipole moment vector in Gaussian has not be selected uniformly for all molecules. To make it uniform, the signs of the vector components should be reversed either for all molecules where this angle is acute or for all molecules where this angle is obtuse (it does not matter which).

With the exception of step 1.2, the current protocol can be applied to aggregates that consist of multiple molecular species. For such systems, the script getMonomers.py would need to be modified, or the system could be split into individual molecules manually. The protocol can also be easily extended to systems that consist of molecules with more than a single bright excited state. The sequence of steps, in this case, would remain unchanged, but a larger number of parameters would need to be calculated: excitation energies for all bright excited states and excitonic couplings between all bright excited states. Modifications to steps 4 and 5 would need to be made accordingly.

The molecular exciton model proposed here only includes Frenkel excitons on the individual molecules in the aggregate or molecular solid and neglects any charge transfer that may occur between molecules. Our earlier work suggests that this approximation is reasonable for aggregates of YLD 124 molecules²⁹. However, in some cases intermolecular charge transfer states may significantly affect the optoelectronic properties of molecular materials⁴⁶. In principle, such charge transfer can be incorporated into exciton models²⁷^,²⁸, albeit at a considerably increased computational cost compared to the case when only Frenkel excitons are accounted for.

In the current model, the effect of molecular vibrations on the optical absorption spectrum is represented by applying Gaussian broadening to the stick spectrum that is calculated using the exciton model. This approximation is rather crude: a more accurate broadening function can be calculated, for instance, by treating the temperature-dependent broadening classically through the sampling of the possible configurations of molecular arrangements in the material (e.g., from molecular dynamics or Monte Carlo simulations) and including the quantum mechanical vibronic contributions as a zero-temperature correction to each vertical transition⁴⁷^,⁴⁸. Alternatively, the spectral density for the vibrational bath that interacts with Frenkel excitons in molecular assemblies can be efficiently calculated using the density functional theory based tight-binding (DFTB) method⁵⁰.

When parametrizing the excitonic Hamiltonian for very large systems, it may be reasonable to only calculate excitonic couplings between molecules that are within some cutoff distance from each other and assume the couplings for molecules at larger distances to be negligibly small. However, when determining this cutoff distance, one must keep in mind that the excitonic couplings depend on the relative orientations of molecules, as well as on the distance between them⁴⁵. For simulating the optoelectronic properties of bulk molecular solids, periodic boundary conditions may be used, so long as the dimensions of the simulated material cell are larger than the cutoff distance for excitonic interactions.

When simulating the optoelectronic properties of bulk molecular solids, it is also important to adequately sample the various possible arrangements of chromophores in the molecular solid. A sufficiently large number of snapshots with representative arrangements of chromophores in the solid sample can be obtained (e.g., from a Monte Carlo simulation of the sample’s microstructure⁵⁰). The calculated optoelectronic properties (e.g., the calculated optical absorption spectra) should then be averaged over all snapshots.

Properties beyond optical absorption spectra can also be computed with the exciton model. For example, the hyperpolarizability of molecular aggregates has been calculated using the exciton approximation to a two-state model³⁰. In addition to the properties of organic materials for optoelectronics, the excitonic Hamiltonians described in this paper are also useful for studying the properties of natural and artificial photosynthetic systems.

Offenlegungen

The authors have nothing to disclose.

Acknowledgements

We thank Dr. Andreas Tillack (Oak Ridge National Laboratory), Dr. Lewis Johnson (University of Washington), and Dr. Bruce Robinson (University of Washington) for developing the program for coarse-grained Monte Carlo simulations that was used to generate the structure of the molecular system presented in the Representative Results section. A.A.K. and P.F.G. are supported by a Collaborative research award from the College of Science, CSU East Bay. M.H. is supported by a Forever Pioneer fellowship from the Center for Student Research, CSU East Bay. C.M.I. and S.S. are supported by the U.S. Department of Defense (Proposal 67310-CH-REP) under the Air Force Office of Scientific Research Organic Materials Division.

Materials

Gaussian 16, revision B1

Multiwfn version 3.3.8

GNU compiler collection version 9.2

python 2.7.0

Referenzen

Tsujimura, T. . OLED Display Fundamentals and Applications, 2nd Ed. , (2017).
Barnes, D. LCD or OLED: Who Wins. SID Symposium Digest of Technical Papers. 44 (1), 26-27 (2013).
Mizukami, M., et al. Flexible Organic Light-Emitting Diode Displays Driven by Inkjet-Printed High-Mobility Organic Thin-Film Transistors. IEEE Electron Device Letters. 39 (1), 39-42 (2018).
Koden, M. . OLED Displays and Lighting. , (2017).
Fan, B., et al. Achieving Over 16% Efficiency for Single-Junction Organic Solar Cells. Science China Chemistry. 62 (6), 746-752 (2018).
Dalton, L. R., Gunter, P., Jazbinsek, M., Kwon, O. P., Sullivan, P. A. . Organic Electro-Optics and Photonics: Molecules, Polymers, and Crystals. , (2015).
Robinson, B. H., et al. Optimization of Plasmonic-Organic Hybrid Electro-Optics. Journal of Lightwave Technology. 36 (21), 5036-5047 (2018).
Yu, D., Yang, Y. Q., Chen, Z., Tao, Y., Liu, Y. F. Recent Progress on Thin-Film Encapsulation Technologies for Organic Electronic Devices. Optics Communications. 362 (1), 43-49 (2016).
Wanapun, D., Hall, V. J., Begue, N. J., Grote, J. G., Simpson, G. J. DNA-Based Polymers as Chiral Templates for Second-Order Nonlinear Optical Materials. ChemPhysChem. 10 (15), 2674-2678 (2009).
Siao, Y. Y., et al. Orderly Arranged NLO Materials on Exfoliated Layered Templates Based on Dendrons with Alternating Moieties at the Periphery. Polymer Chemistry. 4 (9), 2747-2759 (2013).
Sepeai, S., Salleh, M. M., Yahaya, M., Umar, A. A. Improvement of White Organic Light Emitting Diode Performances by an Annealing Process. Thin Solid Films. 517 (16), 4679-4683 (2009).
Mao, G., et al. Considerable Improvement in the Stability of Solution Processed Small Molecule OLED by Annealing. Applied Surface Science. 257 (17), 7394-7398 (2011).
Parr, R. G., Yang, W. . Density Functional Theory of Atoms and Molecules. , (1989).
Dreizlerm, R. M., Gross, E. K. U. . Density Functional Theory: An Approach to the Quantum Many-body Problem. , (1990).
Burke, K., Werschnik, J., Gross, E. K. U. Time-Dependent Density Functional Theory: Past, Present, and Future. Journal of Chemical Physics. 123 (6), 062206 (2005).
Ullrich, C. . Time-Dependent Density-Functional Theory: Concepts and Applications. , (2011).
Vydrov, O. A., Scuseria, G. E. Assessment of a Long-Range Corrected Hybrid Functional. Journal of Chemical Physics. 125 (23), 234109 (2006).
Tawada, Y., Tsuneda, T., Yanagisawa, S. A Long-Range-Corrected Time-Dependent Density Functional Theory. Journal of Chemical Physics. 120 (18), 5425 (2004).
Rohrdanz, M. A., Herbert, J. M. Simultaneous Benchmarking of Ground- and Excited-State Properties with Long-Range-Corrected Density Functional Theory. Journal of Chemical Physics. 129 (3), 034107 (2008).
Autschbach, J. Charge-Transfer Excitations and Time-Dependent Density Functional Theory: Problems and Some Proposed Solutions. ChemPhysChem. 10 (11), 1757-1760 (2008).
Nelson, J., Kwiatkowski, J. J., Kirkpatrick, J., Frost, J. M. Modeling Charge Transport in Organic Photovoltaic Materials. Accounts of Chemical Research. 42 (11), 1768-1778 (2009).
Walker, A. B. Multiscale Modeling of Charge and Energy Transport in Organic Light-Emitting Diodes and Photovoltaics. Proceedings of the IEEE. 97 (9), 1587-1596 (2009).
Wang, L., Li, Q., Shuai, Z., Chenc, L., Shic, Q. Multiscale Study of Charge Mobility of Organic Semiconductor with Dynamic Disorders. Physical Chemistry Chemical Physics. 12 (13), 3309-3314 (2010).
Davydov, A. S. . Theory of Molecular Excitons. , (1971).
Agranovich, V. M. Excitations in Organic Solids. International Series of Monographs on Physics. 142, (2008).
Frenkel, J. On the Transformation of Light into Heat in Solids. I. Physical Review. 37 (1), 17-44 (1931).
Kocherzhenko, A. A., Lee, D., Forsuelo, M. A., Whaley, K. B. Coherent and Incoherent Contributions to Charge Separation in Multichromophore Systems. Journal of Physical Chemistry C. 119 (14), 7590-7603 (2015).
Lee, D., Forsuelo, M. A., Kocherzhenko, A. A., Whaley, K. B. Higher-Energy Charge Transfer States Facilitate Charge Separation in Donor-Acceptor Molecular Dyads. Journal of Physical Chemistry C. 121 (24), 13043-13051 (2017).
Kocherzhenko, A. A., Sosa Vazquez, X. A., Milanese, J. M., Isborn, C. M. Absorption Spectra for Disordered Aggregates of Chromophores Using the Exciton Model. Journal of Chemical Theory and Computation. 13 (8), 3787-3801 (2017).
Kocherzhenko, A. A., et al. Unraveling Excitonic Effects for the First Hyperpolarizabilities of Chromophore Aggregates. Journal of Physical Chemistry C. 123 (22), 13818-13836 (2019).
Krueger, B., Scholes, G., Fleming, G. Calculation of Couplings and Energy-Transfer Pathways between the Pigments of LH2 by the ab Initio Transition Density Cube Method. Journal of Physical Chemistry B. 102 (27), 5378-5386 (1998).
Frisch, M. J., et al. Gaussian 16, Revision B.01. Gaussian, Inc. , (2016).
Lu, T., Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. Journal of Computational Chemistry. 33 (5), 580-592 (2012).
Chai, J. D., Head-Gordon, M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. Journal of Chemical Physics. 128 (8), 084106 (2008).
Hehre, W., Ditchfield, R., Pople, J. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. Journal of Chemical Physics. 56 (5), 2257-2261 (1972).
Hariharan, P., Pople, J. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theoretica chimica acta. 28 (3), 213-222 (1973).
Breneman, C. M., Wiberg, K. B. Determining Atom-Centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis. Journal of Computational Chemistry. 11 (3), 361-373 (1990).
Mulliken, R. S. Electronic Population Analysis on LCAO-MO MolecularWave Functions. I. Journal of Chemical Physics. 23 (10), 1833-1840 (1955).
Jen, A., et al. Exceptional Electro-Optic Properties through Molecular Design and Controlled Self-Assembly. Proceedings of SPIE. 5935, 593506 (2005).
Hirata, S., Head-Gordon, M. Time-Dependent Density Functional Theory Within the Tamm-Dancoff Approximation. Chemical Physics Letters. 314 (3-4), 291-299 (1999).
Randolph, K. A., Myers, L. L. . Basic Statistics in Multivariate Analysis. , 11-34 (2013).
Garrett, K., et al. Optimum Exchange for Calculation of Excitation Energies and Hyperpolarizabilities of Organic Electro-optic Chromophores. Journal of Chemical Theory and Computation. 10 (9), 3821-3831 (2014).
Sekino, H., Maeda, Y. Polarizability and Second Hyperpolarizability Evaluation of Long Molecules by the Density Functional Theory with Long-Range Correction. Journal of Chemical Physics. 126 (1), 014107 (2007).
Johnson, L. E., Dalton, L. R., Robinson, B. H. Optimizing Calculations of Electronic Excitations and Relative Hyperpolarizabilities of Electrooptic Chromophores. Accounts of Chemical Research. 47 (11), 3258-3265 (2014).
Lee, J., et al. Molecular Mechanics Simulations and Improved Tight-Binding Hamiltonians for Artificial Light Harvesting Systems: Predicting Geometric Distributions, Disorder, and Spectroscopy of Chromophores in a Protein Environment. Journal of Physical Chemistry B. 122 (51), 12292-12301 (2018).
Bellinger, D., Pflaum, J., Brüning, C., Engel, V., Engels, B. The Electronic Character of PTCDA Thin Films in Comparison to Other Perylene-Based Organic Semi-conductors: Ab Initio-, TD-DFT and Semi-Empirical Computations of the Opto-Electronic Properties of Large Aggregates. Physical Chemistry Chemical Physics. 19 (3), 2434 (2017).
Zuehlsdorff, T. J., Isborn, C. M. Combining the Ensemble and Franck-Condon Approaches for Calculating Spectral Shapes of Molecules in Solution. The Journal of Chemical Physics. 148 (2), 024110 (2018).
Zuehlsdorff, T. J., Isborn, C. M. Modeling Absorption Spectra of Molecules in Solution. International Journal of Quantum Chemistry. 119 (1), 25719 (2019).
Plötz, P. A., Megow, J., Niehaus, T., Kühn, O. All-DFTB Approach to the Parametrization of the System-Bath Hamiltonian Describing Exciton-Vibrational Dynamics of Molecular Assemblies. Journal of Chemical Theory and Computation. 14 (10), 5001-5010 (2018).
Tillack, A., Johnson, L., Eichinger, B., Robinson, B. H. Systematic Generation of Anisotropic Coarse-Grained Lennard-Jones Potentials and Their Application to Ordered Soft Matter. Journal of Chemical Theory and Computation. 12 (9), 4362-4374 (2016).

Play Video

PDF

DOI

DOWNLOAD MATERIALS LIST

Diesen Artikel zitieren

Kocherzhenko, A. A., Shedge, S. V., Germaux, P. F., Heidarian, M., Isborn, C. M. Excitonic Hamiltonians for Calculating Optical Absorption Spectra and Optoelectronic Properties of Molecular Aggregates and Solids. J. Vis. Exp. (159), e60598, doi:10.3791/60598 (2020).