分子集合体と固体の光吸収スペクトルと光電子特性を計算するためのエキシトニック・ハミルトン人
Summary
ここでは、第一原理量子化学的計算から、光吸収スペクトルと分子材料の光電子特性を計算するための緊密結合型励起性のハミルトンをパラメトリジングするためのプロトコルを提示する。
Abstract
光電子用途のための無秩序な分子集合体および固体の合理的な設計は、理論的および計算的方法を用いてそのような物質の特性を予測する能力に依存している。しかし、障害が大きすぎて摂動限界で考えられない大きな分子系は、第一原理量子化学またはバンド理論を用いて記述することはできません。マルチスケールモデリングは、このようなシステムの光電子特性を理解し、最適化するための有望なアプローチです。第一原理量子化学的手法を用いて個々の分子の特性を計算し、これらの計算に基づいて分子集合体またはバルク物質のモデル・ハミルトンを構築する。本論文では、フレンケル励起子に基づく分子材料の励起状態を表す強固結合型のHamiltonianを構築するためのプロトコルを提示する: 材料を構成する個々の分子に局在する電子正孔対である。ここで提案されたHamiltonianパラメタイゼーションは、分子間の励起的な結合、ならびに周囲の分子上の電荷分布による分子上の電子密度の静電分極化を説明する。このようなモデルのHamiltoniansは、光吸収スペクトルおよび分子凝集体および固体の他の光電子特性を計算するために使用することができる。
Introduction
過去20年間で、凝集した有機分子から作られた固体およびフィルムは、光電子デバイスで複数の用途を発見しました。このような材料に基づくデバイスは、軽量化、柔軟性、低消費電力、インクジェット印刷を使用した安価な生産の可能性など、多くの魅力的な特性を持っています。有機発光ダイオード(OLD)に基づくディスプレイは、液晶ディスプレイを携帯電話、ラップトップ、テレビ、およびその他の電子機器1、2、3、42,の最先端として置き1換えています。3,4照明アプリケーションの OLD の重要性は、今後4年で増加すると予想されます。有機太陽光発電デバイスの性能は着実に改善しており、単接合型有機太陽電池5に対して最近報告された電力変換効率は16%を超えています。有機材料はまた、光ファイバー通信などの他の技術を破壊する可能性があり、その使用により、15 THz以上の66,7以上の非常に高い帯域幅を有する電気光学変調器の開発が可能になる。
オプトエレクトロニクスの用途に向けて固体分子材料を最適化する上での大きな課題は、その特性が一般的に材料のナノスケール構造に大きく依存していることである。製造プロセスでは、化学気相成長、光学活性分子の8個のテンプレート化などの制御された成長技術(すなわち、ポリマーマトリックス99、10)、熱アニーリング11、12、,12などによって、ある程度材料のナノ構造を定義することができます。10しかし、ナノスケールの疾患は、ほとんどの分子材料に固有であり、通常は完全に排除することはできません。したがって、有機光電子材料の合理的な設計には、物質の特性にどのような影響を与えるかを理解し、最適な性能を得るためにそれを設計する方法を見つけることが不可欠です。
分子材料の障害の程度は、通常、バンド理論で記述できる電子構造を有する周期的な結晶構造の摂動として扱うには大きすぎる。一方、バルク材料やフィルムの特性を再現するためにシミュレーションに含まれなければならない分子の数は、密度関数論(DFT)13、14および時間依存密度機能理論(TD-DFT)15,16のような量子化学的方法を第一原理に使用するには大きすぎる。,14 15,16オプトエレクトロニクスに応用されている有機分子は、典型的には、比較的大きなπ共役系を有する。多くはドナーとアクソクターグループを持っています。このような分子における正しい電荷移動挙動を捕捉することは、それらの光電子特性を計算するために不可欠であるが、TD-DFT17、18、19、2018,19,20の17長距離補正ハイブリッド機能を使用してのみ達成することができる。このような機能を用いる計算は、システムの大きさに応じて超直線的にスケールし、現在のところ、〜104未満の原子基底関数を使用して記述できる個々の有機分子または小分子集合体の光電子特性を4モデル化する場合にのみ実用的である。多数のクロモフォアで構成される無秩序な材料を記述できるシミュレーション方法は、これらのシステムをモデル化するのに非常に有用であろう。
分子材料における分子間相互作用の大きさは、多くの場合、材料を構成する個々の分子間のエネルギーパラメータ(固有エネルギーや励起エネルギーなど)の変動の順序に匹敵するか、または小さい。このような場合、マルチスケールモデリングは、大きな障害分子系21,22,23,22の光電子特性を理解し最適化23するための最も有望なアプローチである。このアプローチでは、第一原理量子化学的方法(通常DFTおよびTD-DFT)を用いて、物質を構成する個々の分子の特性を正確に計算します。バルク分子材料を表すのに十分な大きさの材料サンプルのHamiltonian(おそらく、周期的な境界条件を採用することによって)は、個々の分子について計算されたパラメータを使用して構築される。このHamiltonianは、大きな分子集合体、薄膜、またはバルク分子材料の光電子パラメータを計算するために使用することができます。
励起子モデルは、分子材料の励起状態が励起基に表現される多尺度モデルのサブクラスである: クーロンの引力24,2525によって結合される電子正24孔対。多くの励起状態のプロセスをモデル化する場合、電子と正孔が同じ分子に局在するフレンケル励起子26のみを含むだけで十分である。電荷移動励起子は、電子と正孔が異なる分子に局在する場合、場合によっては含める必要がある(例えば、ドナー・アクセプター系における電荷分離をモデル化する場合)27,28。,28励起子モデルは、個々の分子に対する第一原理計算のみを使用してパラメータ化できるマルチスケールモデルですが、分子間相互作用を引き続き説明しています。彼らが説明できる2つの主要な相互作用タイプは、(a)分子間のエキシトン結合または分子間の偏光または分子間の移動能力を特徴付ける分子間の励起的な結合であり、(b)周囲の分子の電荷分布によって分子上の電子密度の静電分極化である。我々は、これらの要因の両方が、光吸収スペクトル29および第1超極極性30のような分子集合体の光学的および電気光学的特性をモデル化するために重要であることを示した。
本論文では、大きな分子集合体やバルク分子材料の光学スペクトルやその他の光電子特性の計算に使用できる、励起子モデルをパラメータ化するためのプロトコルを紹介する。興奮性のハミルトンは、密結合のハミルトン24、25であると25仮定され、
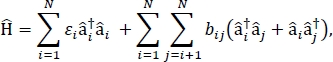
ここでεiは、物質中のi番目の分子の励起エネルギーであり、bijは、i番目とj番目の分子の間の励起的結合であり、âi†と â iはそれぞれ、材料中のi番目の分子の励起状態に対する生成および消滅演算子である。エキシトン・ハミルトンのパラメータは、材料を構成する個々の分子に対して行われるTD-DFT計算を使用して見つかります。これらのTD-DFT計算では、材料内の他のすべての分子の電荷分布は、分子の電子密度の静電分極化を考慮して原子点電荷の静電的埋め込みによって表される。個々の分子に対する励起エネルギー εiは、TD-DFT計算出力から直接取り出される。分子間の励起結合は、bij、b遷移密度キューブ法31を用いて計算され、ガウシアン32におけるTD-DFT計算の出力から得られた相互作用分子の地盤から励起状態への移行密度を有し、Multiwfn多機能波関数アナライザ33を用いて後処理される。バルク分子固形物の特性をシミュレートするために、周期的境界条件を、Hamiltonianに適用してもよい。
現在のプロトコルでは、ユーザがガウス32およびMultiwfn33プログラムにアクセスできる必要があります。このプロトコルはGaussian 16、リビジョンB1、Multiwfnバージョン 3.3.8 を使用してテストされていますが、これらのプログラムの他の最近のバージョンでも動作するはずです。さらに、このプロトコルは、カスタム C++ ユーティリティと、カスタム Python 2.7 および Bash スクリプトを使用 https://github.com/kocherzhenko/ExcitonicHamiltonianします。この計算は、Unix/Linux ファミリのオペレーティング システムを実行しているマシンで実行することを目的としています。
Protocol
Representative Results
Discussion
ここで紹介する方法では、複数のカスタマイズが可能です。たとえば、密度機能、基準セット、原子点電荷の特定の定義など、DFT および TD-DFT 計算のパラメータを変更することができます。
電荷移動文字を使用した遷移に対して合理的な遷移密度を得るために、ωB97X、ωB97XD、ωPBEなどの長い範囲補正機能を使用することをお勧めします。機能的(または正確な交換量や範?…
Disclosures
The authors have nothing to disclose.
Acknowledgements
アンドレアス・ティラック博士(オークリッジ国立研究所)、ルイス・ジョンソン博士(ワシントン大学)、ブルース・ロビンソン博士(ワシントン大学)は、代表結果セクションで提示された分子系の構造を生成するために使用された粗粒度モンテカルロシミュレーションのプログラムを開発してくれたことに感謝します。A.A.K.とP.F.G.は、CSUイーストベイの科学大学の共同研究賞によって支えされています。M.H.は、CSUイーストベイの学生研究センターのフォーエバーパイオニアフェローシップによってサポートされています。C.M.I.と米国は、米国国防総省(提案67310-CH-REP)の下で、空軍科学研究有機材料部門の下で支援されています。
Materials
| Gaussian 16, revision B1 |
| Multiwfn version 3.3.8 |
| GNU compiler collection version 9.2 |
| python 2.7.0 |
References
- Tsujimura, T. . OLED Display Fundamentals and Applications, 2nd Ed. , (2017).
- Barnes, D. LCD or OLED: Who Wins. SID Symposium Digest of Technical Papers. 44 (1), 26-27 (2013).
- Mizukami, M., et al. Flexible Organic Light-Emitting Diode Displays Driven by Inkjet-Printed High-Mobility Organic Thin-Film Transistors. IEEE Electron Device Letters. 39 (1), 39-42 (2018).
- Koden, M. . OLED Displays and Lighting. , (2017).
- Fan, B., et al. Achieving Over 16% Efficiency for Single-Junction Organic Solar Cells. Science China Chemistry. 62 (6), 746-752 (2018).
- Dalton, L. R., Gunter, P., Jazbinsek, M., Kwon, O. P., Sullivan, P. A. . Organic Electro-Optics and Photonics: Molecules, Polymers, and Crystals. , (2015).
- Robinson, B. H., et al. Optimization of Plasmonic-Organic Hybrid Electro-Optics. Journal of Lightwave Technology. 36 (21), 5036-5047 (2018).
- Yu, D., Yang, Y. Q., Chen, Z., Tao, Y., Liu, Y. F. Recent Progress on Thin-Film Encapsulation Technologies for Organic Electronic Devices. Optics Communications. 362 (1), 43-49 (2016).
- Wanapun, D., Hall, V. J., Begue, N. J., Grote, J. G., Simpson, G. J. DNA-Based Polymers as Chiral Templates for Second-Order Nonlinear Optical Materials. ChemPhysChem. 10 (15), 2674-2678 (2009).
- Siao, Y. Y., et al. Orderly Arranged NLO Materials on Exfoliated Layered Templates Based on Dendrons with Alternating Moieties at the Periphery. Polymer Chemistry. 4 (9), 2747-2759 (2013).
- Sepeai, S., Salleh, M. M., Yahaya, M., Umar, A. A. Improvement of White Organic Light Emitting Diode Performances by an Annealing Process. Thin Solid Films. 517 (16), 4679-4683 (2009).
- Mao, G., et al. Considerable Improvement in the Stability of Solution Processed Small Molecule OLED by Annealing. Applied Surface Science. 257 (17), 7394-7398 (2011).
- Parr, R. G., Yang, W. . Density Functional Theory of Atoms and Molecules. , (1989).
- Dreizlerm, R. M., Gross, E. K. U. . Density Functional Theory: An Approach to the Quantum Many-body Problem. , (1990).
- Burke, K., Werschnik, J., Gross, E. K. U. Time-Dependent Density Functional Theory: Past, Present, and Future. Journal of Chemical Physics. 123 (6), 062206 (2005).
- Ullrich, C. . Time-Dependent Density-Functional Theory: Concepts and Applications. , (2011).
- Vydrov, O. A., Scuseria, G. E. Assessment of a Long-Range Corrected Hybrid Functional. Journal of Chemical Physics. 125 (23), 234109 (2006).
- Tawada, Y., Tsuneda, T., Yanagisawa, S. A Long-Range-Corrected Time-Dependent Density Functional Theory. Journal of Chemical Physics. 120 (18), 5425 (2004).
- Rohrdanz, M. A., Herbert, J. M. Simultaneous Benchmarking of Ground- and Excited-State Properties with Long-Range-Corrected Density Functional Theory. Journal of Chemical Physics. 129 (3), 034107 (2008).
- Autschbach, J. Charge-Transfer Excitations and Time-Dependent Density Functional Theory: Problems and Some Proposed Solutions. ChemPhysChem. 10 (11), 1757-1760 (2008).
- Nelson, J., Kwiatkowski, J. J., Kirkpatrick, J., Frost, J. M. Modeling Charge Transport in Organic Photovoltaic Materials. Accounts of Chemical Research. 42 (11), 1768-1778 (2009).
- Walker, A. B. Multiscale Modeling of Charge and Energy Transport in Organic Light-Emitting Diodes and Photovoltaics. Proceedings of the IEEE. 97 (9), 1587-1596 (2009).
- Wang, L., Li, Q., Shuai, Z., Chenc, L., Shic, Q. Multiscale Study of Charge Mobility of Organic Semiconductor with Dynamic Disorders. Physical Chemistry Chemical Physics. 12 (13), 3309-3314 (2010).
- Davydov, A. S. . Theory of Molecular Excitons. , (1971).
- Agranovich, V. M. Excitations in Organic Solids. International Series of Monographs on Physics. 142, (2008).
- Frenkel, J. On the Transformation of Light into Heat in Solids. I. Physical Review. 37 (1), 17-44 (1931).
- Kocherzhenko, A. A., Lee, D., Forsuelo, M. A., Whaley, K. B. Coherent and Incoherent Contributions to Charge Separation in Multichromophore Systems. Journal of Physical Chemistry C. 119 (14), 7590-7603 (2015).
- Lee, D., Forsuelo, M. A., Kocherzhenko, A. A., Whaley, K. B. Higher-Energy Charge Transfer States Facilitate Charge Separation in Donor-Acceptor Molecular Dyads. Journal of Physical Chemistry C. 121 (24), 13043-13051 (2017).
- Kocherzhenko, A. A., Sosa Vazquez, X. A., Milanese, J. M., Isborn, C. M. Absorption Spectra for Disordered Aggregates of Chromophores Using the Exciton Model. Journal of Chemical Theory and Computation. 13 (8), 3787-3801 (2017).
- Kocherzhenko, A. A., et al. Unraveling Excitonic Effects for the First Hyperpolarizabilities of Chromophore Aggregates. Journal of Physical Chemistry C. 123 (22), 13818-13836 (2019).
- Krueger, B., Scholes, G., Fleming, G. Calculation of Couplings and Energy-Transfer Pathways between the Pigments of LH2 by the ab Initio Transition Density Cube Method. Journal of Physical Chemistry B. 102 (27), 5378-5386 (1998).
- Frisch, M. J., et al. Gaussian 16, Revision B.01. Gaussian, Inc. , (2016).
- Lu, T., Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. Journal of Computational Chemistry. 33 (5), 580-592 (2012).
- Chai, J. D., Head-Gordon, M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. Journal of Chemical Physics. 128 (8), 084106 (2008).
- Hehre, W., Ditchfield, R., Pople, J. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. Journal of Chemical Physics. 56 (5), 2257-2261 (1972).
- Hariharan, P., Pople, J. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theoretica chimica acta. 28 (3), 213-222 (1973).
- Breneman, C. M., Wiberg, K. B. Determining Atom-Centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis. Journal of Computational Chemistry. 11 (3), 361-373 (1990).
- Mulliken, R. S. Electronic Population Analysis on LCAO-MO MolecularWave Functions. I. Journal of Chemical Physics. 23 (10), 1833-1840 (1955).
- Jen, A., et al. Exceptional Electro-Optic Properties through Molecular Design and Controlled Self-Assembly. Proceedings of SPIE. 5935, 593506 (2005).
- Hirata, S., Head-Gordon, M. Time-Dependent Density Functional Theory Within the Tamm-Dancoff Approximation. Chemical Physics Letters. 314 (3-4), 291-299 (1999).
- Randolph, K. A., Myers, L. L. . Basic Statistics in Multivariate Analysis. , 11-34 (2013).
- Garrett, K., et al. Optimum Exchange for Calculation of Excitation Energies and Hyperpolarizabilities of Organic Electro-optic Chromophores. Journal of Chemical Theory and Computation. 10 (9), 3821-3831 (2014).
- Sekino, H., Maeda, Y. Polarizability and Second Hyperpolarizability Evaluation of Long Molecules by the Density Functional Theory with Long-Range Correction. Journal of Chemical Physics. 126 (1), 014107 (2007).
- Johnson, L. E., Dalton, L. R., Robinson, B. H. Optimizing Calculations of Electronic Excitations and Relative Hyperpolarizabilities of Electrooptic Chromophores. Accounts of Chemical Research. 47 (11), 3258-3265 (2014).
- Lee, J., et al. Molecular Mechanics Simulations and Improved Tight-Binding Hamiltonians for Artificial Light Harvesting Systems: Predicting Geometric Distributions, Disorder, and Spectroscopy of Chromophores in a Protein Environment. Journal of Physical Chemistry B. 122 (51), 12292-12301 (2018).
- Bellinger, D., Pflaum, J., Brüning, C., Engel, V., Engels, B. The Electronic Character of PTCDA Thin Films in Comparison to Other Perylene-Based Organic Semi-conductors: Ab Initio-, TD-DFT and Semi-Empirical Computations of the Opto-Electronic Properties of Large Aggregates. Physical Chemistry Chemical Physics. 19 (3), 2434 (2017).
- Zuehlsdorff, T. J., Isborn, C. M. Combining the Ensemble and Franck-Condon Approaches for Calculating Spectral Shapes of Molecules in Solution. The Journal of Chemical Physics. 148 (2), 024110 (2018).
- Zuehlsdorff, T. J., Isborn, C. M. Modeling Absorption Spectra of Molecules in Solution. International Journal of Quantum Chemistry. 119 (1), 25719 (2019).
- Plötz, P. A., Megow, J., Niehaus, T., Kühn, O. All-DFTB Approach to the Parametrization of the System-Bath Hamiltonian Describing Exciton-Vibrational Dynamics of Molecular Assemblies. Journal of Chemical Theory and Computation. 14 (10), 5001-5010 (2018).
- Tillack, A., Johnson, L., Eichinger, B., Robinson, B. H. Systematic Generation of Anisotropic Coarse-Grained Lennard-Jones Potentials and Their Application to Ordered Soft Matter. Journal of Chemical Theory and Computation. 12 (9), 4362-4374 (2016).

