Excitonic Hamiltonians for Calculating Optical Absorption Spectra and Optoelectronic Properties of Molecular Aggregates and Solids
Summary
Hier stellen wir ein Protokoll zur Parametrisierung eines eng bindenden exzitonischen Hamiltonian zur Berechnung optischer Absorptionsspektren und optoelektronischer Eigenschaften molekularer Materialien aus quantenchemischen Berechnungen erster Prinzipien vor.
Abstract
Die rationelle Konstruktion ungeordneter molekularer Aggregate und Feststoffe für optoelektronische Anwendungen beruht auf unserer Fähigkeit, die Eigenschaften solcher Materialien mit theoretischen und rechnerischen Methoden vorherzusagen. Große molekulare Systeme, bei denen eine Störung zu signifikant ist, um in der Störgrenze berücksichtigt zu werden, können jedoch weder mit den ersten Prinzipien der Quantenchemie noch mit der Bandtheorie beschrieben werden. Multiscale-Modellierung ist ein vielversprechender Ansatz, um die optoelektronischen Eigenschaften solcher Systeme zu verstehen und zu optimieren. Es verwendet erste Prinzipien quantenchemische Methoden, um die Eigenschaften einzelner Moleküle zu berechnen, dann konstruiert Modell Hamiltonians von molekularen Aggregaten oder Schüttgütern auf der Grundlage dieser Berechnungen. In diesem Beitrag stellen wir ein Protokoll zur Konstruktion eines eng bindenden Hamiltonian vor, das die angeregten Zustände eines molekularen Materials auf der Basis von Frenckel-Exziten darstellt: Elektronen-Loch-Paare, die auf einzelnen Molekülen lokalisiert sind, aus denen das Material besteht. Die hier vorgeschlagene Hamiltonsche Parametrisierung berücksichtigt exzitonische Kopplungen zwischen Molekülen sowie eine elektrostatische Polarisation der Elektronendichte auf einem Molekül durch die Ladungsverteilung auf umgebenden Molekülen. Ein solches Modell Hamiltonians kann verwendet werden, um optische Absorptionsspektren und andere optoelektronische Eigenschaften von molekularen Aggregaten und Feststoffen zu berechnen.
Introduction
In den letzten zwei Jahrzehnten haben Feststoffe und Folien, die aus aggregierten organischen Molekülen hergestellt werden, mehrere Anwendungen in optoelektronischen Geräten gefunden. Geräte, die auf solchen Materialien basieren, haben viele attraktive Eigenschaften, einschließlich geringem Gewicht, Flexibilität, geringem Stromverbrauch und Potenzial für eine billige Produktion mit Inkjet-Druck. Displays, die auf organischen Leuchtdioden (OLEDs) basieren, ersetzen flüssige kristalline Displays als State-of-the-Art für Mobiltelefone, Laptops, Fernsehgeräte und andere elektronische Geräte1,2,3,4. Die Bedeutung von OLEDs für Beleuchtungsanwendungen wird in den kommenden Jahren voraussichtlich zunehmen4. Die Leistung von organischen Photovoltaik-Geräten verbessert sich stetig, mit Leistungsumwandlungseffizienzen von über 16% kürzlich für Ein-Kreuzung organische Solarzellen5gemeldet. Organische Materialien haben auch das Potenzial, andere Technologien zu stören, wie glasfaserkommunikation, wo ihre Verwendung die Entwicklung von elektro-optischen Modulatoren mit extrem hohen Bandbreiten von 15 THz und mehr6,7ermöglicht.
Eine große Herausforderung bei der Optimierung von Festkörper-Molekularmaterialien für Anwendungen in der Optoelektronik besteht darin, dass ihre Eigenschaften in der Regel stark von der nanoskaligen Struktur des Materials abhängen. Der Produktionsprozess ermöglicht die Definition der Nanostruktur eines Materials bis zu einem gewissen Grad durch den Einsatz kontrollierter Wachstumstechniken, wie chemische Dampfabscheidung,8 Verformung von optisch aktiven Molekülen auf ein anderes Material (d.h. eine Polymermatrix9,10), thermisches Glühen11,12usw. Nanoskalenstörungen sind jedoch für die meisten molekularen Materialien intrinsisch und können in der Regel nicht vollständig beseitigt werden. Daher ist es für die rationale Gestaltung organischer optoelektronischer Materialien unerlässlich, zu verstehen, wie sich Unordnung auf die Eigenschaften eines Materials auswirkt, und Wege zu finden, es für eine optimale Leistung zu entwickeln.
Der Grad der Störung in molekularen Materialien ist in der Regel zu groß, um es als Störung einer periodischen kristallinen Struktur mit einer elektronischen Struktur zu behandeln, die durch Bandtheorie beschrieben werden kann. Andererseits ist die Anzahl der Moleküle, die in eine Simulation einbezogen werden müssen, um die Eigenschaften eines Schüttguts oder eines Films zu reproduzieren, zu groß, um erste Prinzipien quantenchemischer Methoden wie Dichtefunktionstheorie (DFT)13,14 und zeitabhängige Dichtefunktionstheorie (TD-DFT)15,16zu verwenden. Organische Moleküle mit Anwendungen in der Optoelektronik haben in der Regel relativ große , konjugierte Systeme; viele haben auch Spender- und Akzeptorgruppen. Die Erfassung des korrekten Ladungsübertragungsverhaltens in solchen Molekülen ist für die Berechnung ihrer optoelektronischen Eigenschaften unerlässlich, kann aber nur mit fernkorrigierten Hybridfunktionen in TD-DFT17,18,19,20erreicht werden. Berechnungen, die solche Funktionen verwenden, skalieren super linear mit der Größe des Systems und sind derzeit nur praktisch, um die optoelektronischen Eigenschaften einzelner organischer Moleküle oder kleiner molekularer Aggregate zu modellieren, die mit nicht mehr als 104 atomaren Basisfunktionen beschrieben werden können. Eine Simulationsmethode, die ungeordnete Materialien beschreiben könnte, die aus einer großen Anzahl von Chromophoren bestehen, wäre sehr nützlich für die Modellierung dieser Systeme.
Die Größe intermolekularer Wechselwirkungen in molekularen Materialien ist oft vergleichbar oder kleiner als die Reihenfolge der Variation der energetischen Parameter (wie die Eigenstate-Energien oder Anregungsenergien) zwischen einzelnen Molekülen, aus denen das Material besteht. In solchen Fällen ist Multiskalenmodellierung der vielversprechendste Ansatz, um die optoelektronischen Eigenschaften großer ungeordneter molekularer Systeme zu verstehen und zu optimieren21,22,23. Dieser Ansatz verwendet quantenchemische Methoden erster Prinzipien (in der Regel DFT und TD-DFT), um die Eigenschaften einzelner Moleküle, aus denen das Material besteht, genau zu berechnen. Der Hamiltonian einer Materialprobe, die groß genug ist, um das Massenmolekülmaterial darzustellen (vielleicht durch die Verwendung periodischer Randbedingungen), wird dann mit den Parametern konstruiert, die für einzelne Moleküle berechnet wurden. Dieser Hamiltonian kann dann verwendet werden, um die optoelektronischen Parameter eines großen molekularen Aggregats, eines dünner Films oder eines Massenmolekülmaterials zu berechnen.
Exciton-Modelle sind eine Unterklasse von Multiskalenmodellen, in denen angeregte Zustände eines molekularen Materials auf der Basis von Exzitendargestellt werden: Elektronenlochpaare, die durch Die Coulomb-Attraktion24,25gebunden sind. Für die Modellierung vieler angeregter Zustandsprozesse reicht es aus, nur Frenkel-Exzitonen26einzubeziehen, bei denen das Elektron und das Loch auf demselben Molekül lokalisiert sind. Ladungsübertragungsexztonen, bei denen das Elektron und das Loch auf verschiedenen Molekülen lokalisiert sind, müssen in einigen Fällen (z. B. bei der Modellierung der Ladungstrennung in Spender-Akzeptor-Systemen)27,28enthalten sein. Obwohl Exciton-Modelle Multiskalenmodelle sind, die nur mit Berechnungen des ersten Prinzips an einzelnen Molekülen parametrisiert werden können, berücksichtigen sie immer noch intermolekulare Wechselwirkungen. Die beiden primären Wechselwirkungstypen, die sie berücksichtigen können, sind (a) exzitonische Kopplungen zwischen Molekülen, die die Fähigkeit von Exziten charakterisieren, sich zwischen Molekülen zu delokalisieren oder zwischen Molekülen zu übertragen, und (b) elektrostatische Polarisation der Elektronendichte auf einem Molekül durch die Ladungsverteilung auf umgebenden Molekülen. Wir haben bereits gezeigt, dass beide Faktoren wichtig für die Modellierung der optischen und elektrooptischen Eigenschaften molekularer Aggregate sind, wie z. B. die optischen Absorptionsspektren29 und die ersten hyperpolarisierbaren30.
In diesem Beitrag stellen wir ein Protokoll zur Parametrisierung von Exzitonmodellen vor, mit dem die optischen Spektren und andere optoelektronische Eigenschaften großer molekularer Aggregate und Massenmolekülmaterialien berechnet werden können. Der excitonic Hamiltonian wird angenommen, dass ein eng bindender Hamiltonian24,25,
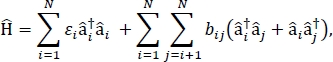
wobei i die Anregungsenergie des i.th Moleküls im Material, bij, die exzitationische Kopplung zwischen den ith- und den jj-th-Molekülen ist, sind i iund ii die Erzeugungs- bzw. Vernichtungsoperatoren für einen angeregten Zustand auf dem ith Molekül im Material.th Die exzitonic Hamiltonian Parameter werden mit TD-DFT-Berechnungen gefunden, die auf einzelnen Molekülen durchgeführt werden, aus denen das Material besteht. In diesen TD-DFT-Berechnungen wird die Ladungsverteilung auf alle anderen Moleküle im Material durch elektrostatische Einbettung von Atompunktladungen dargestellt, um die elektrostatische Polarisation der elektronischen Dichte eines Moleküls zu berücksichtigen. Die Anregungsenergien, ii, für einzelne Moleküle werden direkt aus dem TD-DFT-Berechnungsausgang entnommen. Die excitonischen Kopplungen, bij, zwischen Molekülen werden mit der Transition Density Cube Methode31berechnet, wobei die boden-zu-erregten Zustandsübergangsdichten für die interagierenden Moleküle aus der Ausgabe einer TD-DFT-Berechnung in Gauß-3232 entnommen und mit dem Multiwfn-Multifunktions-Wellenfunktionsanalysator33nachbearbeitet werden. Multiwfn Zur Simulation der Eigenschaften von Massenmolekülfeststoffen können periodische Randbedingungen auf den Hamiltonian angewendet werden.
Das aktuelle Protokoll erfordert, dass der Benutzer Zugriff auf die Programme Gaussian32 und Multiwfn33 hat. Das Protokoll wurde mit Gauß’sche 16, Revision B1 und Multiwfn Version 3.3.8 getestet, sollte aber auch für andere aktuelle Versionen dieser Programme funktionieren. Darüber hinaus verwendet das Protokoll ein benutzerdefiniertes C++-Dienstprogramm und eine Reihe von benutzerdefinierten Python 2.7- und Bash-Skripten, deren Quellcode unter der GNU General Public License (Version 3) zur https://github.com/kocherzhenko/ExcitonicHamiltonian bereitgestellt wird. Die Berechnungen sollen auf einem Computer ausgeführt werden, auf dem ein Betriebssystem aus der Unix/Linux-Familie ausgeführt wird.
Protocol
Representative Results
Discussion
Die hier vorgestellte Methode ermöglicht mehrere Anpassungen. Beispielsweise ist es möglich, die Parameter der DFT- und TD-DFT-Berechnungen zu ändern, einschließlich der Dichtefunktion, des Basissatzes und der spezifischen Definition der Atompunktladungen.
Es wird empfohlen, über weite Strecken korrigierte Funktionen wie z. B97X, B97XD oder PBE zu verwenden, um angemessene Übergangsdichten für Übergänge mit Ladungsübertragungscharakter zu erhalten. Es kann interessant sein zu untersu…
Disclosures
The authors have nothing to disclose.
Acknowledgements
Wir danken Dr. Andreas Tillack (Oak Ridge National Laboratory), Dr. Lewis Johnson (University of Washington) und Dr. Bruce Robinson (University of Washington) für die Entwicklung des Programms für grobkörnige Monte-Carlo-Simulationen, das verwendet wurde, um die Struktur des molekularen Systems zu erzeugen, das im Abschnitt Repräsentative Ergebnisse vorgestellt wurde. A.A.K. und P.F.G. werden durch einen Collaborative Research Award des College of Science, CSU East Bay, unterstützt. M.H. wird von einem Forever Pioneer Stipendium des Center for Student Research, CSU East Bay, unterstützt. C.M.I. und S.S. werden vom US-Verteidigungsministerium (Vorschlag 67310-CH-REP) im Rahmen der Air Force Office of Scientific Research Organic Materials Division unterstützt.
Materials
| Gaussian 16, revision B1 |
| Multiwfn version 3.3.8 |
| GNU compiler collection version 9.2 |
| python 2.7.0 |
References
- Tsujimura, T. . OLED Display Fundamentals and Applications, 2nd Ed. , (2017).
- Barnes, D. LCD or OLED: Who Wins. SID Symposium Digest of Technical Papers. 44 (1), 26-27 (2013).
- Mizukami, M., et al. Flexible Organic Light-Emitting Diode Displays Driven by Inkjet-Printed High-Mobility Organic Thin-Film Transistors. IEEE Electron Device Letters. 39 (1), 39-42 (2018).
- Koden, M. . OLED Displays and Lighting. , (2017).
- Fan, B., et al. Achieving Over 16% Efficiency for Single-Junction Organic Solar Cells. Science China Chemistry. 62 (6), 746-752 (2018).
- Dalton, L. R., Gunter, P., Jazbinsek, M., Kwon, O. P., Sullivan, P. A. . Organic Electro-Optics and Photonics: Molecules, Polymers, and Crystals. , (2015).
- Robinson, B. H., et al. Optimization of Plasmonic-Organic Hybrid Electro-Optics. Journal of Lightwave Technology. 36 (21), 5036-5047 (2018).
- Yu, D., Yang, Y. Q., Chen, Z., Tao, Y., Liu, Y. F. Recent Progress on Thin-Film Encapsulation Technologies for Organic Electronic Devices. Optics Communications. 362 (1), 43-49 (2016).
- Wanapun, D., Hall, V. J., Begue, N. J., Grote, J. G., Simpson, G. J. DNA-Based Polymers as Chiral Templates for Second-Order Nonlinear Optical Materials. ChemPhysChem. 10 (15), 2674-2678 (2009).
- Siao, Y. Y., et al. Orderly Arranged NLO Materials on Exfoliated Layered Templates Based on Dendrons with Alternating Moieties at the Periphery. Polymer Chemistry. 4 (9), 2747-2759 (2013).
- Sepeai, S., Salleh, M. M., Yahaya, M., Umar, A. A. Improvement of White Organic Light Emitting Diode Performances by an Annealing Process. Thin Solid Films. 517 (16), 4679-4683 (2009).
- Mao, G., et al. Considerable Improvement in the Stability of Solution Processed Small Molecule OLED by Annealing. Applied Surface Science. 257 (17), 7394-7398 (2011).
- Parr, R. G., Yang, W. . Density Functional Theory of Atoms and Molecules. , (1989).
- Dreizlerm, R. M., Gross, E. K. U. . Density Functional Theory: An Approach to the Quantum Many-body Problem. , (1990).
- Burke, K., Werschnik, J., Gross, E. K. U. Time-Dependent Density Functional Theory: Past, Present, and Future. Journal of Chemical Physics. 123 (6), 062206 (2005).
- Ullrich, C. . Time-Dependent Density-Functional Theory: Concepts and Applications. , (2011).
- Vydrov, O. A., Scuseria, G. E. Assessment of a Long-Range Corrected Hybrid Functional. Journal of Chemical Physics. 125 (23), 234109 (2006).
- Tawada, Y., Tsuneda, T., Yanagisawa, S. A Long-Range-Corrected Time-Dependent Density Functional Theory. Journal of Chemical Physics. 120 (18), 5425 (2004).
- Rohrdanz, M. A., Herbert, J. M. Simultaneous Benchmarking of Ground- and Excited-State Properties with Long-Range-Corrected Density Functional Theory. Journal of Chemical Physics. 129 (3), 034107 (2008).
- Autschbach, J. Charge-Transfer Excitations and Time-Dependent Density Functional Theory: Problems and Some Proposed Solutions. ChemPhysChem. 10 (11), 1757-1760 (2008).
- Nelson, J., Kwiatkowski, J. J., Kirkpatrick, J., Frost, J. M. Modeling Charge Transport in Organic Photovoltaic Materials. Accounts of Chemical Research. 42 (11), 1768-1778 (2009).
- Walker, A. B. Multiscale Modeling of Charge and Energy Transport in Organic Light-Emitting Diodes and Photovoltaics. Proceedings of the IEEE. 97 (9), 1587-1596 (2009).
- Wang, L., Li, Q., Shuai, Z., Chenc, L., Shic, Q. Multiscale Study of Charge Mobility of Organic Semiconductor with Dynamic Disorders. Physical Chemistry Chemical Physics. 12 (13), 3309-3314 (2010).
- Davydov, A. S. . Theory of Molecular Excitons. , (1971).
- Agranovich, V. M. Excitations in Organic Solids. International Series of Monographs on Physics. 142, (2008).
- Frenkel, J. On the Transformation of Light into Heat in Solids. I. Physical Review. 37 (1), 17-44 (1931).
- Kocherzhenko, A. A., Lee, D., Forsuelo, M. A., Whaley, K. B. Coherent and Incoherent Contributions to Charge Separation in Multichromophore Systems. Journal of Physical Chemistry C. 119 (14), 7590-7603 (2015).
- Lee, D., Forsuelo, M. A., Kocherzhenko, A. A., Whaley, K. B. Higher-Energy Charge Transfer States Facilitate Charge Separation in Donor-Acceptor Molecular Dyads. Journal of Physical Chemistry C. 121 (24), 13043-13051 (2017).
- Kocherzhenko, A. A., Sosa Vazquez, X. A., Milanese, J. M., Isborn, C. M. Absorption Spectra for Disordered Aggregates of Chromophores Using the Exciton Model. Journal of Chemical Theory and Computation. 13 (8), 3787-3801 (2017).
- Kocherzhenko, A. A., et al. Unraveling Excitonic Effects for the First Hyperpolarizabilities of Chromophore Aggregates. Journal of Physical Chemistry C. 123 (22), 13818-13836 (2019).
- Krueger, B., Scholes, G., Fleming, G. Calculation of Couplings and Energy-Transfer Pathways between the Pigments of LH2 by the ab Initio Transition Density Cube Method. Journal of Physical Chemistry B. 102 (27), 5378-5386 (1998).
- Frisch, M. J., et al. Gaussian 16, Revision B.01. Gaussian, Inc. , (2016).
- Lu, T., Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. Journal of Computational Chemistry. 33 (5), 580-592 (2012).
- Chai, J. D., Head-Gordon, M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. Journal of Chemical Physics. 128 (8), 084106 (2008).
- Hehre, W., Ditchfield, R., Pople, J. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. Journal of Chemical Physics. 56 (5), 2257-2261 (1972).
- Hariharan, P., Pople, J. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theoretica chimica acta. 28 (3), 213-222 (1973).
- Breneman, C. M., Wiberg, K. B. Determining Atom-Centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis. Journal of Computational Chemistry. 11 (3), 361-373 (1990).
- Mulliken, R. S. Electronic Population Analysis on LCAO-MO MolecularWave Functions. I. Journal of Chemical Physics. 23 (10), 1833-1840 (1955).
- Jen, A., et al. Exceptional Electro-Optic Properties through Molecular Design and Controlled Self-Assembly. Proceedings of SPIE. 5935, 593506 (2005).
- Hirata, S., Head-Gordon, M. Time-Dependent Density Functional Theory Within the Tamm-Dancoff Approximation. Chemical Physics Letters. 314 (3-4), 291-299 (1999).
- Randolph, K. A., Myers, L. L. . Basic Statistics in Multivariate Analysis. , 11-34 (2013).
- Garrett, K., et al. Optimum Exchange for Calculation of Excitation Energies and Hyperpolarizabilities of Organic Electro-optic Chromophores. Journal of Chemical Theory and Computation. 10 (9), 3821-3831 (2014).
- Sekino, H., Maeda, Y. Polarizability and Second Hyperpolarizability Evaluation of Long Molecules by the Density Functional Theory with Long-Range Correction. Journal of Chemical Physics. 126 (1), 014107 (2007).
- Johnson, L. E., Dalton, L. R., Robinson, B. H. Optimizing Calculations of Electronic Excitations and Relative Hyperpolarizabilities of Electrooptic Chromophores. Accounts of Chemical Research. 47 (11), 3258-3265 (2014).
- Lee, J., et al. Molecular Mechanics Simulations and Improved Tight-Binding Hamiltonians for Artificial Light Harvesting Systems: Predicting Geometric Distributions, Disorder, and Spectroscopy of Chromophores in a Protein Environment. Journal of Physical Chemistry B. 122 (51), 12292-12301 (2018).
- Bellinger, D., Pflaum, J., Brüning, C., Engel, V., Engels, B. The Electronic Character of PTCDA Thin Films in Comparison to Other Perylene-Based Organic Semi-conductors: Ab Initio-, TD-DFT and Semi-Empirical Computations of the Opto-Electronic Properties of Large Aggregates. Physical Chemistry Chemical Physics. 19 (3), 2434 (2017).
- Zuehlsdorff, T. J., Isborn, C. M. Combining the Ensemble and Franck-Condon Approaches for Calculating Spectral Shapes of Molecules in Solution. The Journal of Chemical Physics. 148 (2), 024110 (2018).
- Zuehlsdorff, T. J., Isborn, C. M. Modeling Absorption Spectra of Molecules in Solution. International Journal of Quantum Chemistry. 119 (1), 25719 (2019).
- Plötz, P. A., Megow, J., Niehaus, T., Kühn, O. All-DFTB Approach to the Parametrization of the System-Bath Hamiltonian Describing Exciton-Vibrational Dynamics of Molecular Assemblies. Journal of Chemical Theory and Computation. 14 (10), 5001-5010 (2018).
- Tillack, A., Johnson, L., Eichinger, B., Robinson, B. H. Systematic Generation of Anisotropic Coarse-Grained Lennard-Jones Potentials and Their Application to Ordered Soft Matter. Journal of Chemical Theory and Computation. 12 (9), 4362-4374 (2016).

