Realização de testes de corte em forma de Y montados no microscópio
Summary
O corte em forma de Y mede escalas de comprimento relevantes para fratura e energias em materiais macios. Aparelhos anteriores foram projetados para medições de bancada. Este protocolo descreve a fabricação e o uso de um aparelho que orienta a configuração horizontalmente e fornece as capacidades de posicionamento fino necessárias para a visualização in situ , além da quantificação de falhas, através de um microscópio óptico.
Abstract
O corte em forma de Y demonstrou recentemente ser um método promissor para entender a escala de comprimento limiar e a energia de falha de um material, bem como sua resposta à falha na presença de excesso de energia de deformação. O aparato experimental utilizado nesses estudos foi orientado verticalmente e exigiu passos pesados para ajustar o ângulo entre as pernas em forma de Y. A orientação vertical proíbe a visualização em microscópios ópticos padrão. Este protocolo apresenta um aparelho de corte em forma de Y que se monta horizontalmente sobre um estágio de microscópio invertido existente, pode ser ajustado em três dimensões (X-Y-Z) para se enquadrar no campo de visão do objetivo e permite fácil modificação do ângulo entre as pernas. As duas últimas características são novas para esta técnica experimental. O aparelho apresentado mede a força de corte com precisão de 1 mN. Ao testar o polidimetilsiloxano (PDMS), o material de referência para esta técnica, foi medida uma energia de corte de 132,96 J/m 2 (ângulo de perna de 32°, pré-carga de 75 g) e verificou-se que estava dentro do erro de medições anteriores feitas com uma configuração vertical (132,9 J/m 2 ± 3,4 J/m2). A abordagem se aplica a materiais sintéticos moles, tecidos ou biomembranas e pode fornecer novos insights sobre seu comportamento durante a falha. A lista de peças, arquivos CAD e instruções detalhadas neste trabalho fornecem um roteiro para a fácil implementação dessa poderosa técnica.
Introduction
A mecânica do contínuo não linear forneceu uma lente crítica através da qual entender a concentração de energia que leva à falha em sólidos moles1. No entanto, a predição precisa dessa falha também requer descrições das características microestruturais que contribuem para a criação de novas superfícies na ponta da fissura 2,3. Um método para abordar tais descrições é através da visualização in situ da ponta da fissura durante a falha 4,5. No entanto, o embotamento de rachaduras em testes típicos de fratura de campo distante torna a aquisição de dados in situ desafiadora, espalhando o material altamente deformado, potencialmente fora do campo de visão do microscópio6. O corte em forma de Y oferece uma alternativa única para a visualização microestrutural, pois concentra a região de grande deformação na ponta de uma lâmina7. Além disso, trabalhos anteriores de nosso grupo demonstram que essa abordagem experimental única pode fornecer informações sobre as diferenças na resposta à falha entre o rasgo de campo distante e as condições de carga mediadas por contato7.
O método de corte em forma de Y utilizado no aparelho aqui apresentado foi descrito pela primeira vez décadas atrás como um método de corte para borracha natural8. O método consiste em um corte de lâmina fixa através de uma peça de teste pré-carregada em forma de Y. Na interseção do “Y” está a ponta da rachadura, que é criada antes do teste dividindo uma porção de uma peça retangular em duas “pernas” iguais (Figura 1B e Figura 2D). As principais vantagens deste método de corte incluem a redução das contribuições de atrito para a energia de corte medida, a geometria variável da lâmina (ou seja, a restrição da geometria da ponta da fissura), o controle da taxa de falha (através da taxa de deslocamento da amostra) e o ajuste separado do corte, C e rasgamento, T, contribuições de energia para a energia total Gcortada (ou seja, alterar a energia de falha em excesso de um limiar de corte)8. Estas últimas contribuições são expressas em uma expressão simples e fechada para a energia de corte9
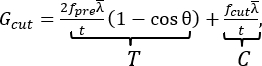 Eqn (1)
Eqn (1)
que utiliza parâmetros selecionados experimentalmente, incluindo a espessura da amostra, t, a deformação média da perna, , a força de pré-carga,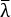 f pre, e o ângulo entre as pernas e o eixo de corte, θ. A força de corte, fcut, é medida com o aparelho, conforme detalhado em Zhang et al.9. Notavelmente, o aparelho apresentado aqui inclui um mecanismo novo, simples e preciso para ajustar o ângulo da perna, θ, e garantir que a amostra esteja centralizada. Embora ambos os recursos sejam críticos para uma configuração montada no microscópio, o mecanismo pode beneficiar futuras implementações verticais do teste de corte em forma de Y, aumentando a facilidade de uso.
f pre, e o ângulo entre as pernas e o eixo de corte, θ. A força de corte, fcut, é medida com o aparelho, conforme detalhado em Zhang et al.9. Notavelmente, o aparelho apresentado aqui inclui um mecanismo novo, simples e preciso para ajustar o ângulo da perna, θ, e garantir que a amostra esteja centralizada. Embora ambos os recursos sejam críticos para uma configuração montada no microscópio, o mecanismo pode beneficiar futuras implementações verticais do teste de corte em forma de Y, aumentando a facilidade de uso.
O progresso na determinação dos critérios de falha apropriados para sólidos moles está em andamento desde o sucesso inicial das geometrias de fratura independentes de amostras introduzidas por Rivlin e Thomas10. Taxas críticas de liberação de energia10, leis de zona coesiva11 e várias formas de abordagens de estresse ou energia à distância12,13,14 têm sido utilizadas. Recentemente, Zhang e Hutchens alavancaram a última abordagem, demonstrando que o corte em forma de Y com lâminas de raio suficientemente pequenas poderia produzir condições de falha de limiar para fratura suave7: uma energia de falha de limiar e uma escala de comprimento de limiar para falha que varia de dezenas a centenas de nanômetros em polidimetilsiloxano homogêneo e altamente elástico (PDMS). Esses resultados foram combinados com a modelagem contínua e a teoria de escala para desenvolver uma relação entre corte e rasgo nesses materiais, demonstrando assim a utilidade do corte em forma de Y para fornecer insights sobre todos os modos de falha suave. No entanto, o comportamento de muitas classes de materiais, incluindo materiais dissipativos e compósitos, permanece inexplorado. Prevê-se que muitos deles exibirão efeitos governados pela microestrutura em escalas de comprimento acima do comprimento de onda da luz visível. Portanto, foi desenhado neste estudo um aparelho que permite a caracterização visual próxima desses efeitos durante o corte em forma de Y pela primeira vez (por exemplo, em compósitos, incluindo tecidos moles, ou de processos dissipativos, previstos nas escalas de comprimento micrômetro a milímetro15).
Protocol
Representative Results
Discussion
O aparato de corte horizontal em forma de Y relatado aqui permite recursos de imagem in situ , juntamente com maior facilidade de uso para essa técnica de falha. O aparelho inclui um design modular/portátil para montagem/desmontagem rápida a partir de um microscópio e ajuste contínuo e pré-alinhado do ângulo das pernas. Todos os arquivos CAD, materiais necessários e procedimentos foram incluídos para facilitar a implementação deste método. Em muitos casos (suportes de lâmina, suporte de amostra, mon…
Disclosures
The authors have nothing to disclose.
Acknowledgements
Gostaríamos de agradecer ao Dr. James Phillips, à Dra. Amy Wagoner-Johnson, a Alexandra Spitzer e a Amir Ostadi por seus conselhos sobre este trabalho. O financiamento veio da bolsa de start-up fornecida pelo Departamento de Ciência Mecânica e Engenharia da Universidade de Illinois Urbana-Champaign. M. Guerena, J. C. Peng, M. Schmid e C. Walsh receberam crédito de design sênior por seu trabalho neste projeto.
Materials
| Buy Parts | |||
| 1" OD Pulley | McMaster Carr | 3434T75 | Pulley for Wire Rope (Larger) |
| 100 g Micro Load Cell | RobotShop | RB-Phi-203 | |
| 1K Resistor | Digi-Key | CMF1.00KFGCT-ND | 1 kOhms ±1% 1 W Through Hole Resistor Axial Flame Retardant Coating, Moisture Resistant, Safety Metal Film |
| 1M Resistor | Digi-Key | RNF14FAD1M00 | 1 MOhms ±1% 0.25 W, 1/4 W Through Hole Resistor Axial Flame Retardant Coating, Safety Metal Film |
| 3/8" OD Pulley | McMaster Carr | 3434T31 | Pulley for Wire Rope |
| 4" Clear Protractor with Easy Read Markings | S&S Worldwide | LR3023 | |
| Breadboard | ECEB | N/A | |
| IC OPAMP ZERO-DRIFT 2 CIRC 8DIP | Digi-Key | LTC1051CN8#PBF-ND | |
| M2 x 0.4 mm Nut | McMaster Carr | 90592A075 | Steel Hex Nut |
| M2 x 0.4 mm x 25 mm | McMaster Carr | 91292A032 | 18-8 Stainless Steel Socket Head Screw |
| M2 x 0.4 mm x 8 mm | McMaster Carr | 91292A832 | 18-8 Stainless Steel Socket Head Screw |
| M3 x 0.5 mm x 15 mm | McMaster Carr | 91290A572 | Black-Oxide Alloy Steel Socket Head Screw |
| M3 x 0.5 mm x 16 mm | McMaster Carr | 91294A134 | Black-Oxide Alloy Steel Hex Drive Flat Head Screw |
| M3 x 0.5 mm, 4 mm High | McMaster Carr | 90576A102 | Medium-Strength Steel Nylon-Insert Locknut |
| M4 x 0.7 mm Nut | McMaster Carr | 90592A090 | Steel Hex Nut |
| M4 x 0.7 mm x 15 mm | McMaster Carr | 91290A306 | Black-Oxide Alloy Steel Socket Head Screw |
| M4 x 0.7 mm x 16 mm | McMaster Carr | 91294A194 | Black-Oxide Alloy Steel Hex Drive Flat Head Screw |
| M4 x 0.7 mm x 18 mm | McMaster Carr | 91290A164 | Black-Oxide Alloy Steel Socket Head Screw |
| M4 x 0.7 mm x 20 mm | McMaster Carr | 91290A168 | Black-Oxide Alloy Steel Socket Head Screw |
| M4 x 0.7 mm x 20 mm | McMaster Carr | 92581A270 | Stell Raised Knurled-Head Thumb Screw |
| M4 x 0.7 mm x 30 mm | McMaster Carr | 91290A172 | Black-Oxide Alloy Steel Socket Head Screw |
| M4 x 0.7 mm x 50 mm | McMaster Carr | 91290A193 | Black-Oxide Alloy Steel Socket Head Screw |
| M4 x 0.7 mm, 5 mm High | McMaster Carr | 94645A101 | High-Strength Steel Nylon-Insert Locknut |
| M5 x 0.8 mm Nut | McMaster Carr | 90592A095 | Steel Hex Nut |
| M5 x 0.8 mm x 16 mm | McMaster Carr | 91310A123 | High-Strength Class 10.9 Steel Hex Head Screw |
| M5 x 0.8 mm x 35 mm | McMaster Carr | 91290A195 | Black-Oxide Alloy Steel Socket Head Screw |
| M5 x 0.8 mm, 13 mm Head Diameter | McMaster Carr | 96445A360 | Flanged Knurled-Head Thumb Nut |
| M5 x 0.8 mm, 5 mm High | McMaster Carr | 90576A104 | Medium-Strength Steel Nylon-Insert Locknut |
| Solidworks | Dassault Systemes | CAD software | |
| Wiring Kit | ECEB | N/A | |
| XYZ Axis Manual Precision Linear Stage 60 mm x 60 mm Trimming Bearing Tuning Platform Sliding Table | OpticsFocus | N/A | |
| Make Parts | |||
| Angle adjustment system- arm | 3D Printing | solidworks: arms_arm_single.SLDPRT QTY: 2 Setting: Fast/0.2 mm layer height |
|
| Angle adjustment system- arms stationary | 3D Printing | solidworks: arms_stationary.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Angle adjustment system- link | 3D Printing | solidworks: arms_arm_link.SLDPRT QTY: 2 Setting: Fast/0.2 mm layer height |
|
| Angle adjustment system- slider | 3D Printing | solidworks: arms_slider.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Angle adjustment system- spacer | 3D Printing | solidworks: arms_front_spacer.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Clip- Blade clip | 3D Printing | solidworks: Blade clip.SLDPRT QTY: 1 Setting: Fine/0.1 mm layer height |
|
| Clip- Blade clip mount | 3D Printing | solidworks: Blade clip mount.SLDPRT QTY: 1 Setting: Fine/0.1 mm layer height |
|
| Frame arm | 3D Printing | solidworks: frame arm.SLDPRT QTY: 2 Setting: Fast/0.2 mm layer height |
|
| Mounting platform | Laser Cut Acrylic | solidworks: mounting platform.SLDPRT QTY: 1 |
|
| Pulley arm (left) | 3D Printing | solidworks: pulley arm_Mirror.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Pulley arm (right) | 3D Printing | solidworks: pulley arm.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Sample holder and tab- Clamp | 3D Printing | solidworks: Clamp.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Sample holder and tab- Sample holder | 3D Printing | solidworks: Sample holder.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Sample holder and tab- Tab | 3D Printing | solidworks: Tab.SLDPRT QTY: 2 per test Setting: Fine/0.1 mm layer height, no brim |
|
| Vertical adjust system- Inner slide | 3D Printing | solidworks: Inner slide.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
|
| Vertical adjust system- Outer slide | 3D Printing | solidworks: Outer slide.SLDPRT QTY: 1 Setting: Fast/0.2 mm layer height |
References
- Long, R., Hui, C. -. Y. Crack tip fields in soft elastic solids subjected to large quasi-static deformation – A review. Extreme Mechanics Letters. 4, 131-155 (2015).
- Slootman, J., et al. Quantifying rate-and temperature-dependent molecular damage in elastomer fracture. Physical Review X. 10, 041045 (2020).
- Zhao, X., et al. Soft materials by design: Unconventional polymer networks give extreme properties. Chemical Review. 121 (8), 4309-4372 (2021).
- Mzabi, S., Berghezan, D., Roux, S., Hild, F., Creton, C. A critical local energy release rate criterion for fatigue fracture of elastomers. Journal of Polymer Science Part B: Polymer Physics. 49 (21), 1518-1524 (2011).
- Chen, Y., Mellot, G., Van Luijk, D., Creton, C., Sijbesma, R. P. Mechanochemical tools for polymer materials. Chemical Society Reviews. 50, 4100-4140 (2021).
- Hui, C. -. Y., Jagota, A., Bennison, S. J., Londono, J. D. Crack blunting and the strength of soft elastic solids. Proceedings of the Royal Society A Mathematical, Physical and Engineering Science. 459 (2034), 1489-1516 (2003).
- Zhang, B., Hutchens, S. B. On the relationship between cutting and tearing in soft elastic solids. Soft Matter. 17, 6728-6741 (2021).
- Lake, G. J., Yeoh, O. H. Measurement of rubber cutting resistance in the absence of friction. International Journal of Fracture. 14, 509-526 (1978).
- Zhang, B., Shiang, C. -. S., Yang, S. J., Hutchens, S. B. Y-shaped cutting for the systematic characterization of cutting and tearing. Experimental Mechanics. 59, 517-529 (2019).
- Rivlin, R. S., Thomas, A. G. Rupture of rubber. I. Characteristic energy for tearing. Journal of Polymer Science. 10 (3), 291-318 (1953).
- Elices, M., Guinea, G. V., Gómez, J., Planas, J. The cohesive zone model: Advantages, limitations and challenges. Engineering Fracture Mechanics. 69 (2), 137-163 (2002).
- Taylor, D. . The Theory of Critical Distances. , (2007).
- Williams, J. G. Stress at a distance fracture criteria and crack self-blunting in rubber. International Journal of Non-Linear Mechanics. 68, 33-36 (2015).
- Talamini, B., Mao, Y., Anand, L. Progressive damage and rupture in polymers. Journal of the Mechanics and Physics of Solids. 111, 434-457 (2018).
- Long, R., Hui, C. -. Y., Gong, J. P., Bouchbinder, E. The fracture of highly deformable soft materials: A tale of two length scales. Annual Review of Condensed Matter Physics. 12, 71-94 (2021).
- Gent, A. N., Wang, C. Cutting resistance of polyethylene. Journal of Polymer Science: Part B: Polymer Physics. 34 (13), 2231-2237 (1996).
- Chen, X., Nadiarynkh, O., Plotnikov, S., Campagnola, P. J. Second harmonic generation microscopy for quantitative analysis of collagen fibrillar structure. Nature Protocols. 7, 654-669 (2015).
- Pan, B., Qian, K., Xie, H., Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Measurements Science and Technology. 20 (6), 062001 (2009).

