Caracterización espectral y magneto-óptica resuelta en ángulo de nanoestructuras fotónicas
Summary
La estructura de la banda fotónica permite comprender cómo se propagan los modos electromagnéticos confinados dentro de un cristal fotónico. En los cristales fotónicos que incorporan elementos magnéticos, estos modos ópticos confinados y resonantes van acompañados de una actividad magneto-óptica mejorada y modificada. Describimos un procedimiento de medición para extraer la estructura de la banda magneto-óptica mediante la microscopía espacial Fourier.
Abstract
Los cristales fotónicos son nanoestructuras periódicas que pueden soportar una variedad de modos electromagnéticos confinados. Estos modos confinados suelen ir acompañados de una mejora local de la intensidad del campo eléctrico que fortalece las interacciones entre la luz y la materia, lo que permite aplicaciones como la dispersión de Raman (SERS) mejorada en superficie y la sensibilidad mejorada de plasmón superficial. En presencia de materiales magneto-ópticamente activos, la mejora del campo local da lugar a una actividad magneto-óptica anómala. Típicamente, los modos confinados de un cristal fotónico dado dependen fuertemente de la longitud de onda y el ángulo de incidencia de la radiación electromagnética incidente. Por lo tanto, se necesitan mediciones espectrales y resueltas angularmente para identificarlas plenamente, así como para establecer su relación con la actividad magneto-óptica del cristal. En este artículo, describimos cómo utilizar un microscopio de plano de Fourier (plano focal posterior) para caracterizar muestras magnetoópticamente activas. Como sistema de modelos, aquí utilizamos una rejilla plasmónica construida a partir de magneto-ópticamente activo Au/Co/Au multicapa. En los experimentos, aplicamos un campo magnético en la rejilla in situ y medimos su respuesta espacial recíproca, obteniendo la respuesta magneto-óptica de la rejilla en un rango de longitudes de onda y ángulos de incidencia. Esta información nos permite construir un mapa completo de la estructura plasmónica de la banda de la rejilla y el ángulo y la longitud de onda dependiente actividad magneto-óptica. Estas dos imágenes nos permiten precisar el efecto que las resonancias plasmal tienen en la respuesta magneto-óptica de la rejilla. La magnitud relativamente pequeña de los efectos magneto-ópticos requiere un tratamiento cuidadoso de las señales ópticas adquiridas. Con este fin, se establece un protocolo de procesamiento de imágenes para obtener una respuesta magneto-óptica a partir de los datos sin procesar adquiridos.
Introduction
Los modos electromagnéticos confinados en cristales fotónicos pueden surgir de una variedad de orígenes diferentes, tales como resonancias plasmón alrededor de interfaces metálicas/dieléctricas o resonancias Mie en nanoestructuras dieléctricas de alto índice de refracción1,2,3, y pueden ser diseñados para aparecer en frecuencias definidas específicamente4,5. Su presencia da lugar a muchos fenómenos fascinantes como las brechas de banda fotónica6,7,8, fuerte localización de fotones9, luz lenta10 y conos Dirac11. La microscopía de plano y la espectroscopia de Fourier son herramientas básicas para la caracterización de nanoestructuras fotónicas, ya que permiten capturar muchas propiedades esenciales de los modos confinados que se producen en ellas. En la microscopía espacial Fourier, a diferencia de las imágenes planas reales convencionales, la información se presenta como la función de las coordenadas angulares12,13. Alternativamente se conoce como imagen del plano focal posterior (BFP), ya que la descomposición angular de la luz que emana de la muestra se registra desde el plano focal posterior del objetivo del microscopio. El espectro angular, es decir, el patrón de emisión de campo lejano de la muestra está relacionado con el impulso de la luz que emana de ella (ak). En particular, representa su distribución de impulso en plano (kx,ky)14.
En muestras magnetoópticamente activas, se ha demostrado que la presencia de excitaciones fotónicas confinadas da como resultado una mejora considerable de la respuesta magneto-óptica15,16,17,18,19. Los efectos magnetoópticos dependen de la geometría mutua del campo magnético y de la radiación electromagnética incidente. Las geometrías magneto-ópticas más comúnmente encontradas para la luz polarizada linealmente y su nomenclatura se representan en la Figura 1. Aquí, demostramos una configuración que se puede utilizar para explorar dos efectos magneto-ópticos que se observan en la reflexión: efectos de Kerr magnetoópticos transversales y longitudinales, abreviados, respectivamente, como TMOKE y LMOKE. TMOKE es un efecto de intensidad, donde las reflectividades de los estados de magnetización opuestos son diferentes, mientras que LMOKE se manifiesta como una rotación del eje de polarización de luz reflejada. Los efectos se distinguen por la orientación de la magnetización con respecto a la incidencia de luz, donde para LMOKE, la magnetización se orienta paralela al componente plano del vector de onda de la luz mientras que para TMOKE es transversal a ella. Para la luz normalmente incidente, ambos componentes en el plano del impulso de la luz son nulos (kx x ky 0) y, en consecuencia, ambos efectos son cero. Las configuraciones en las que ambos efectos están presentes se pueden concebir fácilmente. Sin embargo, para simplificar el análisis de datos, en esta demostración nos limitamos a situaciones en las que sólo uno de los efectos está presente, a saber, TMOKE.
Se pueden utilizar varias configuraciones ópticas para medir la distribución angular de la luz emitida por los cristales magnetofotónicos. Por ejemplo, en Kalish et al.20 y Borovkova et al.21, tal configuración se utilizó con éxito en la geometría de transmisión para revelar la influencia del plasmón en los fenómenos magneto-ópticos. A modo de ilustración, en Kurvits et al.22, se presentan algunas configuraciones posibles para un microscopio que utiliza una lente objetivo corregida infinitamente. En nuestra configuración, representada en la Figura 2A,utilizamos una lente corregida infinita donde la luz procedente de un punto dado de la muestra es dirigida por la lente objetivo en haces colineales. En la Figura 2A, las vigas que emergen de la parte superior (líneas discontinuas) y la parte inferior (líneas sólidas) de la muestra se representan esquemáticamente. A continuación, se utiliza una lente de recogida para reenfocar estos haces para formar una imagen en el plano de imagen (IP). Una segunda lente, también conocida como lente Bertrand, se coloca después del plano de imagen para separar la luz entrante en su plano focal en componentes angulares, representados en la Figura 2A en rojo, azul y negro. Desde este plano focal posterior, la distribución angular de la luz emitida por la muestra se puede medir con una cámara. Efectivamente, la lente Bertrand realiza una transformación de Fourier en el haz de luz que llega a él. La distribución de intensidad espacial en el BFP corresponde a la distribución angular de la radiación incidente. Se puede establecer un mapa completo de reflectancia espacial recíproca de la muestra iluminando la muestra con el mismo objetivo que se utiliza para recoger la respuesta de la muestra. Las vigas de entrada y salida se separan mediante un divisor de vigas. La configuración completa se representa en la figura 3A. Para obtener un espectro, se necesita una fuente de luz ajustable o un monocromático. La medición se puede repetir a través de diferentes longitudes de onda, teniendo en cuenta que debido al espectro de fuentes de luz estándar, los resultados deben normalizarse a la reflectividad de una muestra de control. Para este propósito, se puede utilizar un espejo o una parte de la muestra que se ha dejado sin patrones a propósito para permitir una alta reflectividad. Para ayudar en el posicionamiento, mostramos cómo integrar la configuración con un sistema óptico adicional que permite la creación de imágenes en el espacio real de la muestra, que se muestra en la Figura 2B.
Procedemos ahora a establecer un método para medir el espectro magneto-óptico resuelto angular de un cristal fotónico, utilizando como muestra representativa, una rejilla de DVD cubierta con una película Au/Co/Au donde la presencia de cobalto ferromagnético da lugar a una considerable actividad magneto-óptica23. La ondulación periódica de la rejilla de DVD permite resonancias de polaritón plasmónico de superficie (SPP) en combinaciones de longitud de onda y ángulo distintas que son dadas por
donde n es el índice de refracción del entorno circundante, k0 el vector de onda de la luz en el espacio libre,0 el ángulo de incidencia, d la periodicidad de la rejilla y m es un entero que denota el orden del SPP. El vector de onda 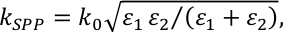 SPP se da por dondelos valoresde 1 y2 son las permitistividades de la capa metálica y el entorno dieléctrico circundante. Debido al grosor de la película multicapa de oro/cobalto, podemos suponer que los SPP sólo se excitan en cima de la película multicapa.
SPP se da por dondelos valoresde 1 y2 son las permitistividades de la capa metálica y el entorno dieléctrico circundante. Debido al grosor de la película multicapa de oro/cobalto, podemos suponer que los SPP sólo se excitan en cima de la película multicapa.
Protocol
Representative Results
Discussion
Hemos introducido una configuración de medición y un protocolo para obtener espectros magnetoópticos resueltos angularmente de cristales ópticos. En particular, se ha establecido el caso de los materiales ferromagnéticos, que requiere un análisis de datos adicional para tener en cuenta la permeabilidad no lineal del material. La espectroscopia magneto-óptica resuelta angular presenta una ventaja adicional sobre los métodos resueltos no angulares de que los modos confinados pueden identificarse más fácilmente a …
Disclosures
The authors have nothing to disclose.
Acknowledgements
Reconocemos el apoyo financiero del Ministerio de Economía y Competitividad a través de los proyectos MAT2017-85232-R (AEI/FEDER,UE), Severo, Ochoa (SEV-2015-0496) y por la Generalitat de Catalunya (2017, SGR 1377), por el CNPq – Brasil, y por la Comisión Europea (Marie Sk-odowska-Curie IF EMPHASIS – DLV-748429).
Materials
| Beam splitter | Thorlabs | BSW27 | |
| Bertrand lens | Thorlabs | LA1608 | f = 75 mm |
| CCD Camera | Thorlabs | 1500M-GE-TE | Camera for real space imaging |
| Collecting lens | Thorlabs | ITL200 | f = 200 mm |
| Collimating lens | Zeiss | 420640-9800 | Magnification 10x NA 0.3 |
| Flip mirror | Thorlabs | CCM1-P01/M | |
| Flip mirror mount | Thorlabs | FM90/M | |
| L1-lens | Thorlabs | LA1986 | f = 125 mm |
| L2-lens | Thorlabs | LA1461 | f = 250 mm |
| Objective lens | Nikon | MUE10500 | Magnification 50x NA 0.8 |
| Pinhole | Thorlabs | ID8/M | |
| Polarizer | Thorlabs | GTH10M | For LMOKE measurements, two polarizers are needed |
| sCMOS camera | Andor | ZYLA-4.2P-USB3 |
References
- Bayer, M., et al. Optical Modes in Photonic Molecules. Physical Review Letters. 81 (12), 2582-2585 (1998).
- Blanco, A., et al. Large-scale synthesis of a silicon photonic crystal with a complete three-dimensional bandgap near 1.5 micrometres. Nature. 405 (6785), 437 (2000).
- Rybin, M. V., et al. High-Q Supercavity Modes in Subwavelength Dielectric Resonators. Physical Review Letters. 119 (24), 243901 (2017).
- Joannopoulos, J. D., Villeneuve, P. R., Fan, S. Photonic crystals. Solid State Communications. 102 (2), 165-173 (1997).
- Englund, D., Fushman, I., Vuckovic, J. General recipe for designing photonic crystal cavities. Optics Express. 13 (16), 5961-5975 (2005).
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Physical Review Letters. 58 (20), 2059-2062 (1987).
- Yablonovitch, E. Photonic band-gap structures. JOSA B. 10 (2), 283-295 (1993).
- Noda, S., Tomoda, K., Yamamoto, N., Chutinan, A. Full Three-Dimensional Photonic Bandgap Crystals at Near-Infrared Wavelengths. Science. 289 (5479), 604-606 (2000).
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Physical Review Letters. 58 (23), 2486-2489 (1987).
- Krauss, T. F. Slow light in photonic crystal waveguides. Journal of Physics D: Applied Physics. 40 (9), 2666-2670 (2007).
- Huang, X., Lai, Y., Hang, Z. H., Zheng, H., Chan, C. T. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nature Materials. 10 (8), 582-586 (2011).
- Wagner, R., Heerklotz, L., Kortenbruck, N., Cichos, F. Back focal plane imaging spectroscopy of photonic crystals. Applied Physics Letters. 101 (8), 081904 (2012).
- Zhang, D., et al. Back focal plane imaging of directional emission from dye molecules coupled to one-dimensional photonic crystals. Nanotechnology. 25 (14), 145202 (2014).
- Vasista, A. B., Sharma, D. K., Kumar, G. V. P. Fourier Plane Optical Microscopy and Spectroscopy. Digital Encyclopedia of Applied Physics. , 1-14 (2019).
- Belotelov, V. I., Doskolovich, L. L., Zvezdin, A. K. Extraordinary Magneto-Optical Effects and Transmission through Metal-Dielectric Plasmonic Systems. Physical Review Letters. 98 (7), 077401 (2007).
- Belotelov, V. I., et al. Enhanced magneto-optical effects in magnetoplasmonic crystals. Nature Nanotechnology. 6 (6), 370 (2011).
- Chetvertukhin, A. V., et al. Magneto-optical Kerr effect enhancement at the Wood’s anomaly in magnetoplasmonic crystals. Journal of Magnetism and Magnetic Materials. 324 (21), 3516-3518 (2012).
- Kataja, M., et al. Surface lattice resonances and magneto-optical response in magnetic nanoparticle arrays. Nature Communications. 6, 7072 (2015).
- Kataja, M., et al. Hybrid plasmonic lattices with tunable magneto-optical activity. Optics Express. 24 (4), 3652-3662 (2016).
- Kalish, A. N., et al. Magnetoplasmonic quasicrystals: an approach for multiband magneto-optical response. Optica. 5 (5), 617-623 (2018).
- Borovkova, O. V., et al. TMOKE as efficient tool for the magneto-optic analysis of ultra-thin magnetic films. Applied Physics Letters. 112 (6), 063101 (2018).
- Kurvits, J. A., Jiang, M., Zia, R. Comparative analysis of imaging configurations and objectives for Fourier microscopy. JOSA A. 32 (11), 2082-2092 (2015).
- Cichelero, R., Oskuei, M. A., Kataja, M., Hamidi, S. M., Herranz, G. Unexpected large transverse magneto-optic Kerr effect at quasi-normal incidence in magnetoplasmonic crystals. Journal of Magnetism and Magnetic Materials. 476, 54-58 (2019).
- Cichelero, R., Kataja, M., Campoy-Quiles, M., Herranz, G. Non-reciprocal diffraction in magnetoplasmonic gratings. Optics Express. 26 (26), 34842-34852 (2018).
- Melo, L. G. C., Santos, A. D., Alvarez-Prado, L. M., Souche, Y. Optimization of the TMOKE response using the ATR configuration. Journal of Magnetism and Magnetic Materials. 310 (2, Part 3), e947-e949 (2007).
- Regatos, D., Sepúlveda, B., Fariña, D., Carrascosa, L. G., Lechuga, L. M. Suitable combination of noble/ferromagnetic metal multilayers for enhanced magneto-plasmonic biosensing. Optics Express. 19 (9), 8336-8346 (2011).
- Polisetty, S., et al. Optimization of magneto-optical Kerr setup: Analyzing experimental assemblies using Jones matrix formalism. Review of Scientific Instruments. 79 (5), 055107 (2008).
- Sato, K. Measurement of Magneto-Optical Kerr Effect Using Piezo-Birefringent Modulator. Japanese Journal of Applied Physics. 20 (12), 2403 (1981).

