Caractérisation spectrale et optique de la caractérisation spectrale et angle des nanostructures photoniques
Summary
La structure de la bande photonique permet de comprendre comment les modes électromagnétiques confinés se propagent dans un cristal photonique. Dans les cristaux photoniques qui incorporent des éléments magnétiques, ces modes optiques confinés et résonnants sont accompagnés d’une activité magnéto-optique améliorée et modifiée. Nous décrivons une procédure de mesure pour extraire la structure magnéto-optique de bande par la microscopie d’espace de Fourier.
Abstract
Les cristaux photoniques sont des nanostructures périodiques qui peuvent supporter une variété de modes électromagnétiques confinés. Ces modes confinés sont généralement accompagnés d’une amélioration locale de l’intensité du champ électrique qui renforce les interactions lumière-matière, permettant des applications telles que la diffusion Raman (SERS) améliorée par surface et la détection améliorée du plasmon de surface. En présence de matériaux magnéto-optiques actifs, l’amélioration du champ local donne lieu à une activité magnéto-optique anormale. Typiquement, les modes confinés d’un cristal photonique donné dépendent fortement de la longueur d’onde et de l’angle d’incidence du rayonnement électromagnétique incident. Ainsi, des mesures spectrales et angulaires sont nécessaires pour les identifier pleinement ainsi que pour établir leur relation avec l’activité magnéto-optique du cristal. Dans cet article, nous décrivons comment utiliser un microscope de Quatre-plan (plan focal arrière) pour caractériser des échantillons magnéto-optiquement actifs. En tant que système modèle, nous utilisons ici une grille plasmonique construite à partir de magnéto-optiquement active Au/Co/Au multicouche. Dans les expériences, nous appliquons un champ magnétique sur la grille in situ et mesurons sa réponse spatiale réciproque, obtenant la réponse magnéto-optique de la grille sur une gamme de longueurs d’onde et d’angles d’incident. Cette information nous permet de construire une carte complète de la structure de la bande plasmonique de la grille et de l’angle et de la longueur d’onde dépendant de l’activité magnéto-optique. Ces deux images nous permettent d’identifier l’effet que les résonances plasmonontes ont sur la réponse magnéto-optique de la grille. L’ampleur relativement faible des effets magnéto-optiques nécessite un traitement minutieux des signaux optiques acquis. À cette fin, un protocole de traitement d’image pour obtenir la réponse magnéto-optique des données brutes acquises est établi.
Introduction
Les modes électromagnétiques confinés dans les cristaux photoniques peuvent provenir d’une variété d’origines différentes, telles que les résonances plasmon autour des interfaces métal/diélectrique ou les résonances Mie dans les nanostructures diélectriques à indice réfractif élevé1,2,3, et peuvent être conçus pour apparaître à des fréquences spécifiquement définies4,5. Leur présence donne lieu à de nombreux phénomènes fascinants tels que les lacunes bande photonique6,7,8, forte localisation photon9, lumière lente10 et Cônes Dirac11. La microscopie et la spectroscopie de plan De plus sont des outils de base pour caractériser les nanostructures photoniques car elles permettent de capturer de nombreuses propriétés essentielles des modes confinés qui s’y trouvent. Dans la microscopie spatiale de Fourier, par opposition à l’imagerie classique de plan réel, l’information est présentée comme la fonction des coordonnées angulaires12,13. Il est également connu sous le nom de plan focal arrière (BFP) imagerie que la décomposition angulaire de la lumière émanant de l’échantillon est enregistrée à partir du plan focal arrière de l’objectif du microscope. Le spectre angulaire, c’est-à-dire le modèle d’émission de champ éloigné de l’échantillon est lié à l’élan de la lumière qui en émane(k). En particulier, il représente son élan dans l’avion (kx,ky)distribution14.
Dans les échantillons magnéto-optiquement actifs, la présence d’excitations photoniques confinées a été montrée pour avoir comme conséquence l’amélioration considérable de la réponse magnéto-optique15,16,17,18,19. Les effets magnéto-optiques dépendent de la géométrie mutuelle du champ magnétique et du rayonnement électromagnétique incident. Les géométries magnéto-optiques les plus couramment rencontrées pour la lumière polarisée linéairement et leur nomenclature sont représentées dans la figure 1. Ici, nous démontrons une configuration qui peut être utilisée pour explorer deux effets magnéto-optiques qui sont observés dans la réflexion: transversal et longitudinal magnéto-optique effets Kerr, abrégé, respectivement, comme TMOKE et LMOKE. TMOKE est un effet d’intensité, où les réflectivités des états de magnétisation opposés sont différentes tandis que LMOKE se manifeste comme une rotation de l’axe de polarisation de la lumière réfléchie. Les effets se distinguent par l’orientation de la magnétisation par rapport à l’incidence de la lumière, où pour LMOKE, la magnétisation est orientée parallèlement à la composante plan dans le vecteur d’onde de la lumière tandis que pour TMOKE il est transversal à elle. Pour la lumière incidente normale, les deux composants de l’élan de lumière sont nuls (kx ky et 0) et, par conséquent, les deux effets sont nuls. Les configurations où les deux effets sont présents peuvent être facilement conçues. Cependant, pour simplifier l’analyse des données, dans cette démonstration, nous nous limitons à des situations où un seul des effets est présent, à savoir TMOKE.
Plusieurs configurations optiques peuvent être utilisées pour mesurer la distribution angulaire de la lumière émise par les cristaux magnétophotoniques. Par exemple, dans Kalish et coll.20 et Borovkova etal. 21, une telle configuration a été utilisée avec succès dans la géométrie de transmission pour dévoiler l’influence du plasmon sur les phénomènes magnéto-optiques. À titre d’illustration, dans Kurvits et coll.22, certaines configurations possibles sont présentées pour un microscope qui utilise une lentille objective corrigée à l’infini. Dans notre configuration, représentée dans la figure 2A, nous utilisons une lentille corrigée à l’infini où la lumière provenant d’un point donné dans l’échantillon est dirigée par la lentille objective dans les faisceaux collinear. Dans la figure 2A, les poutres émergeant du haut (lignes pointillées) et le fond (lignes solides) de l’échantillon sont représentés schématiquement. Ensuite, une lentille de collecte est utilisée pour recentrer ces faisceaux pour former une image au plan d’image (IP). Une deuxième lentille, également connue sous le nom de lentille Bertrand, est ensuite placée après le plan d’image pour séparer la lumière entrante à son plan focal en composants angulaires, représentés dans la figure 2A en rouge, bleu et noir. À partir de ce plan focal arrière, la distribution angulaire de la lumière émise par l’échantillon peut être mesurée à l’aide d’une caméra. En effet, l’objectif Bertrand effectue une transformation Fourier sur le faisceau lumineux qui y arrive. La répartition de l’intensité spatiale au BFP correspond à la distribution angulaire du rayonnement incident. Une carte complète de la réflectoflage de l’espace réciproque de l’échantillon peut être établie en illuminant l’échantillon avec le même objectif qui est utilisé pour recueillir la réponse de l’échantillon. Les faisceaux entrants et sortants sont séparés à l’aide d’un séparateur de faisceaux. La configuration complète est représentée dans la figure 3A. Pour obtenir un spectre, une source lumineuse réglable ou un monochromator est nécessaire. La mesure peut ensuite être répétée sur différentes longueurs d’onde, en gardant à l’esprit qu’en raison du spectre des sources lumineuses standard, les résultats doivent être normalisés à la réflectivité d’un échantillon témoin. À cette fin, on peut utiliser un miroir ou une partie de l’échantillon qui a été délibérément laissé sans motif pour permettre une réflectivité élevée. Pour faciliter le positionnement, nous montrons comment intégrer la configuration à un système optique supplémentaire qui permet l’imagerie de l’espace réel de l’échantillon, illustrée dans la figure 2B.
Nous procédons maintenant à l’établissement d’une méthode pour mesurer le spectre magnéto-optique résolu angulaire d’un cristal photonique, en utilisant comme échantillon représentatif, une grille DE DVD recouverte d’un film Au/Co/Au où la présence de cobalt ferromagnetic donne lieu à une activité magnéto-optique considérable23. L’ondulation périodique de la grille DVD permet des résonances de polariton de plasmon de surface (SPP) à des combinaisons distinctes de longueur d’onde-angle qui sont données par
où n est l’indice de réfraction de l’environnement environnant, k0 le vecteur d’onde de la lumière dans l’espace libre,0 l’angle d’incidence, d la périodicité de la grille et m est un entier dénotant l’ordre du SPP. Le vecteur d’onde 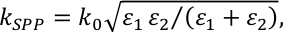 SPP est donné par l’endroit où les permis de la couche métallique et de l’environnement diélectrique environnant sont les permis. En raison de l’épaisseur du film multicouche or/cobalt, nous pouvons supposer que les SPP ne sont excités qu’au-dessus du film multicouche.
SPP est donné par l’endroit où les permis de la couche métallique et de l’environnement diélectrique environnant sont les permis. En raison de l’épaisseur du film multicouche or/cobalt, nous pouvons supposer que les SPP ne sont excités qu’au-dessus du film multicouche.
Protocol
Representative Results
Discussion
Nous avons introduit une configuration de mesure et un protocole pour obtenir des spectres magnéto-optiques résolus angulaires de cristaux optiques. En particulier, le cas des matériaux ferromagnetic, qui nécessite une analyse supplémentaire des données pour tenir compte de la perméabilité non linéaire du matériau, a été présenté. La spectroscopie magnéto-optique résolue angulaire présente un avantage supplémentaire par rapport aux méthodes non-angulaires résolues que les modes confinés peuvent être…
Disclosures
The authors have nothing to disclose.
Acknowledgements
Nous reconnaissons le soutien financier du ministre espagnol d’Economa y Competitividad à travers des projets MAT2017-85232-R (AEI/FEDER,UE), Severo, Ochoa (SEV-2015-0496) et par la Generalitat de Catalunya (2017, SGR 1377), par le CNPq – Brésil, et par la Commission européenne (Marie Skôodowska-Curie IF EMPHASIS – DLV-748429).
Materials
| Beam splitter | Thorlabs | BSW27 | |
| Bertrand lens | Thorlabs | LA1608 | f = 75 mm |
| CCD Camera | Thorlabs | 1500M-GE-TE | Camera for real space imaging |
| Collecting lens | Thorlabs | ITL200 | f = 200 mm |
| Collimating lens | Zeiss | 420640-9800 | Magnification 10x NA 0.3 |
| Flip mirror | Thorlabs | CCM1-P01/M | |
| Flip mirror mount | Thorlabs | FM90/M | |
| L1-lens | Thorlabs | LA1986 | f = 125 mm |
| L2-lens | Thorlabs | LA1461 | f = 250 mm |
| Objective lens | Nikon | MUE10500 | Magnification 50x NA 0.8 |
| Pinhole | Thorlabs | ID8/M | |
| Polarizer | Thorlabs | GTH10M | For LMOKE measurements, two polarizers are needed |
| sCMOS camera | Andor | ZYLA-4.2P-USB3 |
References
- Bayer, M., et al. Optical Modes in Photonic Molecules. Physical Review Letters. 81 (12), 2582-2585 (1998).
- Blanco, A., et al. Large-scale synthesis of a silicon photonic crystal with a complete three-dimensional bandgap near 1.5 micrometres. Nature. 405 (6785), 437 (2000).
- Rybin, M. V., et al. High-Q Supercavity Modes in Subwavelength Dielectric Resonators. Physical Review Letters. 119 (24), 243901 (2017).
- Joannopoulos, J. D., Villeneuve, P. R., Fan, S. Photonic crystals. Solid State Communications. 102 (2), 165-173 (1997).
- Englund, D., Fushman, I., Vuckovic, J. General recipe for designing photonic crystal cavities. Optics Express. 13 (16), 5961-5975 (2005).
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Physical Review Letters. 58 (20), 2059-2062 (1987).
- Yablonovitch, E. Photonic band-gap structures. JOSA B. 10 (2), 283-295 (1993).
- Noda, S., Tomoda, K., Yamamoto, N., Chutinan, A. Full Three-Dimensional Photonic Bandgap Crystals at Near-Infrared Wavelengths. Science. 289 (5479), 604-606 (2000).
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Physical Review Letters. 58 (23), 2486-2489 (1987).
- Krauss, T. F. Slow light in photonic crystal waveguides. Journal of Physics D: Applied Physics. 40 (9), 2666-2670 (2007).
- Huang, X., Lai, Y., Hang, Z. H., Zheng, H., Chan, C. T. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nature Materials. 10 (8), 582-586 (2011).
- Wagner, R., Heerklotz, L., Kortenbruck, N., Cichos, F. Back focal plane imaging spectroscopy of photonic crystals. Applied Physics Letters. 101 (8), 081904 (2012).
- Zhang, D., et al. Back focal plane imaging of directional emission from dye molecules coupled to one-dimensional photonic crystals. Nanotechnology. 25 (14), 145202 (2014).
- Vasista, A. B., Sharma, D. K., Kumar, G. V. P. Fourier Plane Optical Microscopy and Spectroscopy. Digital Encyclopedia of Applied Physics. , 1-14 (2019).
- Belotelov, V. I., Doskolovich, L. L., Zvezdin, A. K. Extraordinary Magneto-Optical Effects and Transmission through Metal-Dielectric Plasmonic Systems. Physical Review Letters. 98 (7), 077401 (2007).
- Belotelov, V. I., et al. Enhanced magneto-optical effects in magnetoplasmonic crystals. Nature Nanotechnology. 6 (6), 370 (2011).
- Chetvertukhin, A. V., et al. Magneto-optical Kerr effect enhancement at the Wood’s anomaly in magnetoplasmonic crystals. Journal of Magnetism and Magnetic Materials. 324 (21), 3516-3518 (2012).
- Kataja, M., et al. Surface lattice resonances and magneto-optical response in magnetic nanoparticle arrays. Nature Communications. 6, 7072 (2015).
- Kataja, M., et al. Hybrid plasmonic lattices with tunable magneto-optical activity. Optics Express. 24 (4), 3652-3662 (2016).
- Kalish, A. N., et al. Magnetoplasmonic quasicrystals: an approach for multiband magneto-optical response. Optica. 5 (5), 617-623 (2018).
- Borovkova, O. V., et al. TMOKE as efficient tool for the magneto-optic analysis of ultra-thin magnetic films. Applied Physics Letters. 112 (6), 063101 (2018).
- Kurvits, J. A., Jiang, M., Zia, R. Comparative analysis of imaging configurations and objectives for Fourier microscopy. JOSA A. 32 (11), 2082-2092 (2015).
- Cichelero, R., Oskuei, M. A., Kataja, M., Hamidi, S. M., Herranz, G. Unexpected large transverse magneto-optic Kerr effect at quasi-normal incidence in magnetoplasmonic crystals. Journal of Magnetism and Magnetic Materials. 476, 54-58 (2019).
- Cichelero, R., Kataja, M., Campoy-Quiles, M., Herranz, G. Non-reciprocal diffraction in magnetoplasmonic gratings. Optics Express. 26 (26), 34842-34852 (2018).
- Melo, L. G. C., Santos, A. D., Alvarez-Prado, L. M., Souche, Y. Optimization of the TMOKE response using the ATR configuration. Journal of Magnetism and Magnetic Materials. 310 (2, Part 3), e947-e949 (2007).
- Regatos, D., Sepúlveda, B., Fariña, D., Carrascosa, L. G., Lechuga, L. M. Suitable combination of noble/ferromagnetic metal multilayers for enhanced magneto-plasmonic biosensing. Optics Express. 19 (9), 8336-8346 (2011).
- Polisetty, S., et al. Optimization of magneto-optical Kerr setup: Analyzing experimental assemblies using Jones matrix formalism. Review of Scientific Instruments. 79 (5), 055107 (2008).
- Sato, K. Measurement of Magneto-Optical Kerr Effect Using Piezo-Birefringent Modulator. Japanese Journal of Applied Physics. 20 (12), 2403 (1981).

