Ajuste de los límites de supersimetría Usar modelos simplificados

Una de las extensiones más prometedores del Modelo Estándar, la supersimetría (SUSY) ^1-14, es el foco central de muchas búsquedas por los experimentos del LHC en el CERN. Los datos recogidos en el año 2011 ya son suficientes para empujar los límites de la nueva física más allá de las de cualquier colisionador anterior ^15-22. A medida que llegan nuevos datos y las exclusiones son empujados aún más lejos, cada vez será más importante comunicar claramente a la comunidad de la física lo regiones del extenso espacio de parámetros supersimétrica han sido excluidos. Los límites actuales se establecen normalmente en constreñidos planos bidimensionales, que con frecuencia no representan el espacio de parámetros SUSY disponibles diversos y difíciles de entender, los límites a las masas físicas o fracciones de ramificación. Un gran conjunto de modelos simplificados ^{23, 24} se han propuesto para ayudar en la comprensión de estos límites, y ambos ATLAS y CMS han proporcionado resultados de exclusión de varios de estos modelos ^15-20.

En este trabajo se demuestra la aplicación de estas exclusiones modelo simplificado de un modelo de la física nueva completa con el ejemplo de la supergravedad mínima (mSUGRA, también conocido como el CMSSM) ^25-30. Este modelo se elige con el fin de comparar los límites establecidos usando modelos simplificados a los publicados de forma independiente por los experimentos. El procedimiento es lo suficientemente generales como para ser extensible a cualquier nuevo modelo de la física (NPM). Como este es el primer intento de "cerrar el círculo" y establecer límites a SUSY utilizando modelos simplificados, una serie de supuestos acerca de la aplicabilidad de los límites en determinados modelos simplificados son explorados, lo que resulta en las recetas para el establecimiento de límites conservadores y agresivos en las teorías que tienen no fueron examinados por los experimentos del LHC.

Para establecer un límite de un mecanismo nacional de prevención, se requieren tres operaciones separadas. En primer lugar, el mecanismo nacional de prevención debe ser deconstruido sus partes constitutivas, separando los diferentes productoresmodos cción y modos de desintegración para todas las nuevas partículas en el modelo. En segundo lugar, un conjunto de modelos simplificados debe ser elegido para recrear la cinemática y topologías de eventos relevantes en el MNP. En tercer lugar, los límites disponibles en estos modelos simplificados deben combinarse para producir límites en el MNP. Estos tres procedimientos se describen en el protocolo. Algunas aproximaciones adicionales también se ofrecen que pueden ampliar la aplicabilidad de los modelos simplificados ya disponibles para una amplia gama de topologías de eventos.

Una completa NPM implica típicamente muchos modos de producción y muchos posibles decaimientos posteriores. La deconstrucción de los nuevos modelos de la física en sus componentes y la aplicación de los límites de modelos simplificados para estos componentes permite la construcción de una exclusión limita directamente. Para cualquier región de la señal, el límite de la mayoría conservadora se puede establecer mediante la fracción de la producción de P _{(a, b)} (donde a, b representa el modelo de spa simplificadamodo de producción Artículo) de eventos idénticos a un modelo simplificado i y la fracción ramificada para los spartículas producidos a la decadencia de la manera descrita por el modelo † simplificado, BR _{a → i} x BR _{b → i.} El número esperado de eventos en una región determinada señal de estos sencillos topologías se puede escribir como

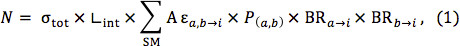
donde la suma es sobre modelos simplificados, _tot σ es la sección eficaz total para el punto de la NGP, L _int es la luminosidad integrada utilizada en la búsqueda, y AE _{a, b → i} es la aceptación veces la eficiencia de los sucesos modelo simplificado en el región señal que está siendo considerado. Este número se puede comparar con el límite superior nivel de confianza del 95% que se espera en el número de nuevos eventos de física to seleccione la región de búsqueda óptima. El modelo puede entonces ser excluida si N es mayor que el número observado de nuevos eventos de física excluidos en el nivel de confianza del 95%. Exclusiones en regiones no superpuestas se pueden combinar si la información sobre las correlaciones de sus incertidumbres está disponible. Si esta información no está disponible, la mejor región señal o el análisis que proporciona la mejor límite de espera se pueden utilizar para intentar excluir el modelo.

Para construir límites concretos con este método, el Aε para varios modelos simplificados debe ponerse a disposición por los experimentos del LHC. Tanto la CMS y ATLAS han publicado cifras con el Aε para varios modelos, y algunas de las figuras están disponibles en la base de datos HepData ^31. Con el fin de demostrar el valor de la publicación de todos estos cuadros, creemos que es importante proporcionar a los límites concretos que son comparables a las ya publicadas. Por ello utilizamos (y describiendoe en el protocolo como un paso opcional) una simulación detector rápido para emular el efecto del ATLAS o detector CMS. El Aε derivado de la Bastante Buena Simulación (PGS) ³² se compara con el publicado por ATLAS en una cuadrícula modelo simplificado en la figura 1. Estos resultados son lo suficientemente cerca uno del otro (a menos de aproximadamente el 25%) que, en lugar de esperar a que todos los resultados sean públicos, resultados Aε para las redes restantes se obtienen a partir de PGS y se utilizan directamente en el resto de este artículo. Como el número de disponibles públicamente modelo simplificado resultados Aε crece, la necesidad de tales aproximaciones se debe reducir de manera significativa.

Dos supuestos conservadores permiten la inclusión de un mayor número de modos de producción y de decaimiento en el límite. La primera es que para la producción asociada la Aε experimental es por lo menos tan alta como la Aε para el peor de los dos modos de producción. ParaBúsquedas inclusivas, esto es generalmente una buena suposición. El número mínimo de eventos previsto sería entonces

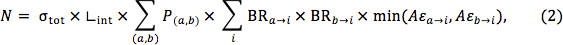
donde la primera suma se extiende sobre todos los modos de producción, y sólo aquellos en los que a y b son exactamente las partículas del modelo simplificado se incluyen en la Ecuación 1. Del mismo modo, la Aε para decae con diferentes piernas se puede suponer que ser al menos tan alta como la Aε para la peor de las dos piernas. Es decir,

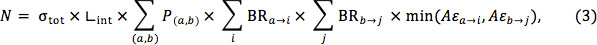
donde ahora se han incluido diagramas con diferentes decaimientos a cada lado.

Otros dos supuestos permitirían el establecimiento de strlímites icter. Uno puede asumir que el Aε experimental para todos los modos de producción en la teoría es similar a la Aε promedio de los modos de producción cubiertos por modelos simplificados. En ese caso, el número esperado de eventos en lugar se puede escribir como

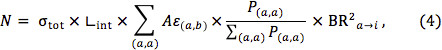
cuando las sumas son a la vez más de sólo los modos de producción cubiertos por modelos simplificados. Se podría suponer, además, que la Aε para todos los modos de desintegración en la teoría es similar a la Aε promedio para esos eventos cubiertos por las topologías modelo simplificado. A continuación, el número esperado de eventos puede ser escrito como:

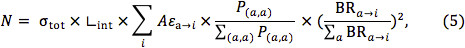
donde agapor las cuantías que se ejecutan sólo en los modelos simplificados. Claramente, se proporciona el límite mSUGRA más agresivo en este supuesto, y un límite establecido de esta manera los riesgos de reclamar la exclusión de regiones que no, de hecho, ser excluidos en el nivel de confianza del 95% mediante una búsqueda específica. Aunque la exactitud de estas dos aproximaciones puede ser sospechoso, si la cinemática de eventos inclusivos de los modelos simplificados se comparan favorablemente con un punto espacio de parámetros SUSY completa, puede que no sean razonables.

† Algunos modelos simplificados que ahora se utilizan en el LHC incluyen la producción asociada. Si bien no se discuten explícitamente aquí, las ecuaciones pueden ser trivialmente extendidos para permitir que para este caso.