12.6:
Rigid Body Equilibrium Problems – II
JoVE 비디오를 활용하시려면 도서관을 통한 기관 구독이 필요합니다. 전체 비디오를 보시려면 로그인하거나 무료 트라이얼을 시작하세요.
JoVE 핵심
물리학
Rigid Body Equilibrium Problems – II
5,579 Views
•
01:21 min
•
April 30, 2023
A rigid body is in static equilibrium when the net force and the net torque acting on the system are equal to zero.
Consider two children sitting on a seesaw, which has negligible mass. The first child has a mass (m1) of 26 kg and sits at point A, which is 1.6 meters (r1) from the pivot point B; the second child has a mass (m2) of 32 kg and sits at point C. How far from the pivot point B should the second child sit (r2) to balance the seesaw?
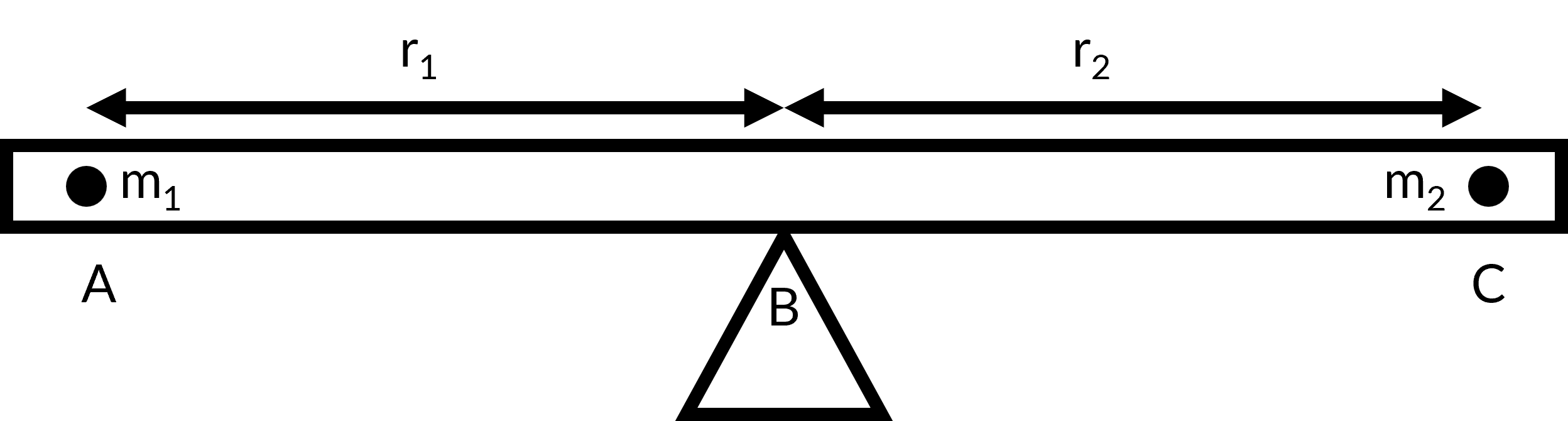
In order to solve the problem, the steps for rigid body equilibrium must be followed:
- Identify the seesaw and two children as the system of interest. Consider the supporting pivot to be the point about which the torques are calculated and all external forces are acting on the system.
- Draw a free-body diagram for the object, including all the forces that act on the system. Here, the three external forces acting on the system are the weights of the two children and the supporting force of the pivot. Now, the torque produced at each point A, C, and B are m1r1, −m2r2, and zero (as the pivot point is the point at which torque is calculated), respectively. The minus sign for m2r2 is due to the torque acting in a clockwise direction.
- Apply the second condition for equilibrium, where the sum of the torques in the system is zero. Substituting the values in the equation, the distance is determined as 1.3 m.
This text is adapted from Openstax, University Physics Volume 1, Section 12.2: Examples of Static Equilibrium.
