11.14:
Structures of Solids
11,416 Views
•
•
Solids in which the atoms, ions, or molecules are arranged in a definite repeating pattern are known as crystalline solids. Metals and ionic compounds typically form ordered, crystalline solids. A crystalline solid has a precise melting temperature because each atom or molecule of the same type is held in place with the same forces or energy. Amorphous solids or non-crystalline solids (or, sometimes, glasses) which lack an ordered internal structure and are randomly arranged. Substances that consist of large molecules, or a mixture of molecules whose movements are more restricted, often form amorphous solids. Amorphous material undergoes gradual softening, over a range of temperatures, due to the structural non-equivalence of the molecules. When an amorphous material is heated, the weakest intermolecular attractions break first. As the temperature is increased further, the stronger attractions are broken.
Unit Cell
The structure of a crystalline solid is best described by its simplest repeating unit, referred to as its unit cell. The unit cell consists of lattice points that represent the locations of atoms or ions. The entire structure then consists of this unit cell repeating in three dimensions, as illustrated in Figure 1.
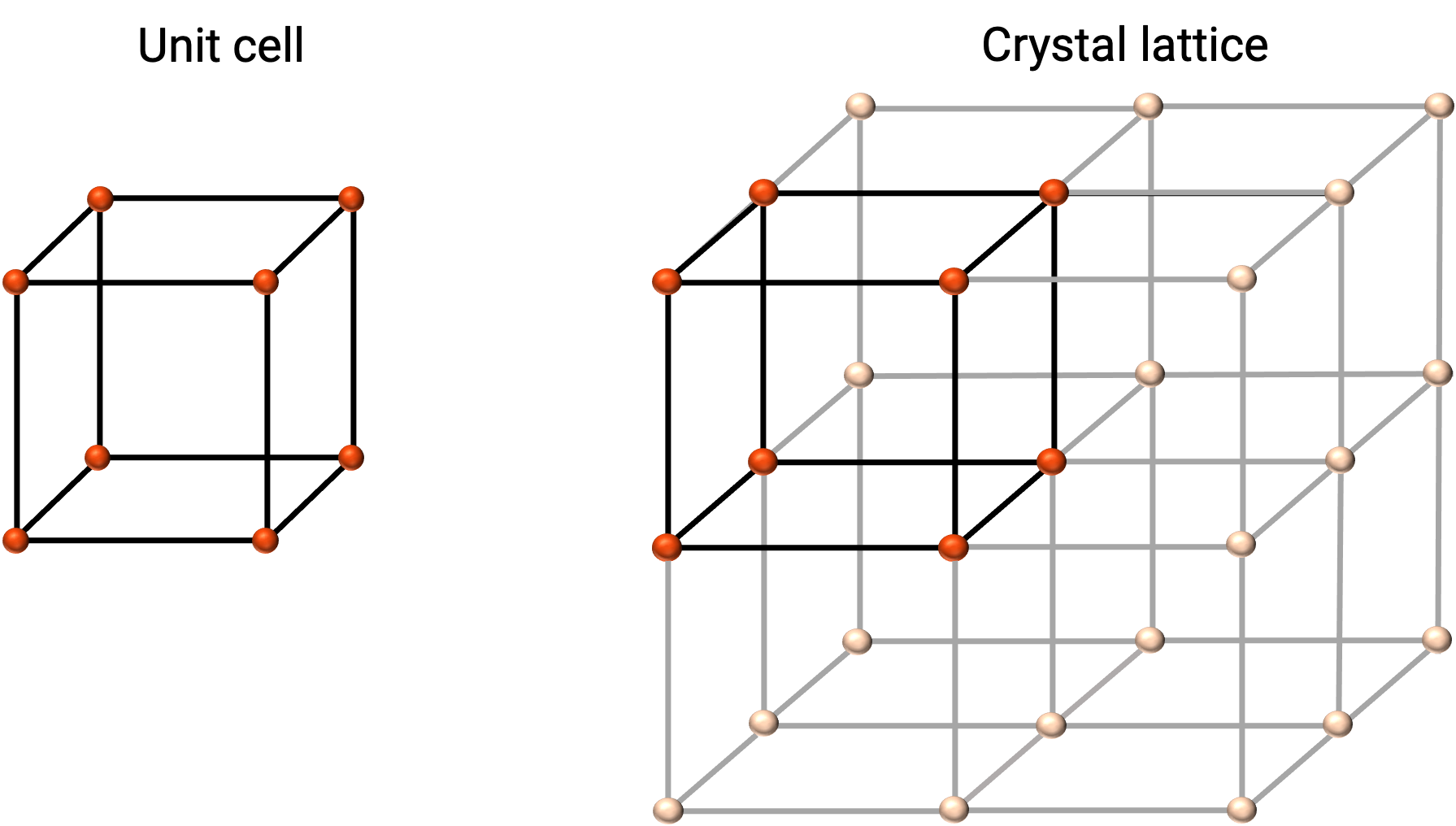
Figure 1. Unit cell and crystal lattice with lattice points indicated in red.
In general, a unit cell is defined by the lengths of three axes (a, b, and c) and the angles (α, β, and γ) between them as shown in Figure 2. The axes are defined as being the lengths between points in the space lattice.
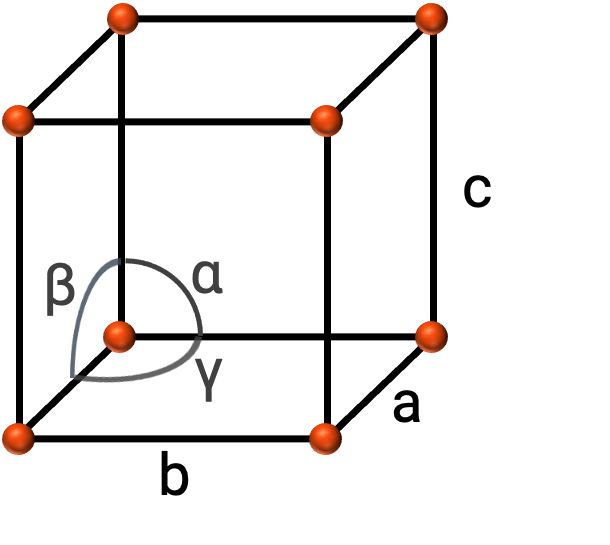
Figure 2. Unit cell is defined by its axes (a, b, and c), and angles (α, β, and γ)
There are seven different lattice systems, some of which have more than one type of lattice, for a total of fourteen different unit cells.
| Systems | Angles | Axes |
| Cubic | α = β = γ = 90° | a = b = c |
| Tetragonal | α = β = γ = 90° | a = b ≠ c |
| Orthorhombic | α= β = γ = 90° | a ≠ b ≠ c |
| Monoclinic | α = γ = 90°; β ≠ 90° | a ≠ b ≠ c |
| Triclinic | α ≠ β ≠ γ ≠ 90° | a ≠ b ≠ c |
This text is adapted from Openstax, Chemistry 2e, Section 10.6: Lattice Structures in Crystalline Solids.
