Shaping the Amplitude and Phase of Laser Beams by Using a Phase-only Spatial Light Modulator
Özet
We show how to encode the complex field of laser beams by using a single phase element. A common-path interferometer is employed to mix the phase information displayed into a phase-only spatial light modulator to finally retrieve the desired complex field pattern at the output of an optical imaging system.
Abstract
The aim of this article is to visually demonstrate the utilization of an interferometric method for encoding complex fields associated with coherent laser radiation. The method is based on the coherent sum of two uniform waves, previously encoded into a phase-only spatial light modulator (SLM) by spatial multiplexing of their phases. Here, the interference process is carried out by spatial filtering of light frequencies at the Fourier plane of certain imaging system. The correct implementation of this method allows arbitrary phase and amplitude information to be retrieved at the output of the optical system.
It is an on-axis, rather than off-axis encoding technique, with a direct processing algorithm (not an iterative loop), and free from coherent noise (speckle). The complex field can be exactly retrieved at the output of the optical system, except for some loss of resolution due to the frequency filtering process. The main limitation of the method might come from the inability to operate at frequency rates higher than the refresh rate of the SLM. Applications include, but are not limited to, linear and non-linear microscopy, beam shaping, or laser micro-processing of material surfaces.
Introduction
Almost all laser applications are in close relation with the management of the optical wavefront of light. In the paraxial approximation, the complex field associated with the laser radiation can be described by two terms, the amplitude and the phase. Having control over these two terms is necessary to modify both the temporal and the spatial structure of laser beams at will. In general, the amplitude and the phase of a laser beam can be properly changed by several methods including the use of optical components that range from single bulk lenses, beam splitters and mirrors to most complex devices like deformable mirrors or spatial light modulators. Here, we show a method for encoding and reconstructing the complex field of coherent laser beams, which is based on dual-phase hologram theory1, and the utilization of a common-path interferometer.
Nowadays, there exists a wide variety of methods to encode the complex fields of laser beams2,3,4,5. In this context, some well-established methods to produce phase and amplitude modulation rely on the use of digital holograms6. A common point in all these methods is the necessity of generating a spatial offset to separate the desired output beam from the zeroth-order coming from the reflection of light at the SLM display. These methods are basically off-axis (usually applying for the first diffraction order of the grating), employing phase grating not only to encode the phase, but also to introduce necessary amplitude modulation. In particular, amplitude modulation is performed by spatially lowering the grating height, which clearly degrades the diffraction efficiency. The hologram reconstruction process mostly gets an approximate, but not exact, reconstruction of the amplitude and phase of the desired complex field. Discrepancies between theory and experiment seem to appear from an inaccurate encoding of the amplitude information as well as other experimental issues happening during the spatial filtering of the first diffraction order or due to SLM pixilation effects. In addition, the intensity profile of the input beam can introduce restrictions on the output power.
In contrast, with the introduced method7, all light management is carried out on-axis, which is very convenient from an experimental point of view. Additionally, it takes advantage of considering, in the paraxial approximation, the complex field associated with laser beams as a sum of two uniform waves. The amplitude information is synthetized by the interference of these uniform waves. In practice, such interference is carried out by spatial filtering of light frequencies at the Fourier plane of a given imaging system. Previously, the phase patterns associated with the uniform waves are spatially multiplexed and encoded into a phase-only SLM (placed at the entrance plane of this imaging system). Hence, the whole optical setup can be regarded as a common-path interferometer (very robust against mechanical vibrations, temperature changes, or optical misalignments). Please, note that the abovementioned interference process can be alternatively accomplished by using other optical layouts: with a couple of phase-only SLMs properly placed within a typical two-arm interferometer, or by time sequentially encoding the two phase patterns into the SLM (previous introduction of a reference mirror in the optical setup). In both cases, there is no necessity of spatial filtering, and consequently no loss of spatial resolution, at the expense of increasing the complexity of the optical system, as well as the alignment process. Here, it should be also emphasized that by using this encoding method, the full spectrum of the desired complex field can be exactly retrieved at the Fourier plane, after filtering all diffraction orders but the zeroth one.
On the other hand, the efficiency of the method depends on several factors: the manufacturer's specifications of the SLM (e.g., fill factor, reflectivity, or diffraction efficiency), the size of the encoded pattern, and the way at which the light impinges onto the SLM (reflection with a small hitting angle, or normal incidence by using a beam splitter). At this point, under proper experimental conditions, the measured total light efficiency can be more than 30%. However, note that that the total light efficiency just due to the use of the SLM can be less than 50%. The lack of random or diffuser elements within the optical setup allows the retrieving of amplitude and phase patterns without coherent noise (speckle). Other significant aspects to point out are the utilization of a direct codification algorithm rather than iterative procedures and its ability to perform arbitrary and independent amplitude and phase modulation at the frequency refresh time of the SLM (up to hundreds of hertz according to the current technology).
In principle, the method7 is intended to be used with input plane waves, but it is not limited to that. For instance, if a Gaussian beam is hitting the SLM, it is possible to modify its irradiance shape at the output of the system by encoding a suited amplitude pattern into the SLM. However, as the intensity of the output beam cannot exceed that of the input beam at any transversal position (x,y), the shaping of the amplitude is performed by intensity losses originated by a partially destructive interference process.
The theory underlining the encoding method7 is as follows. Any complex field represented in the form U(x,y)= A(x,y)eiφ(x,y) can be also rewritten as:
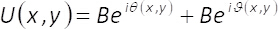 (1)
(1)
where
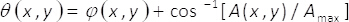 (2)
(2)
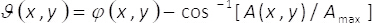 (3)
(3)
In equations 1-3, the amplitude and phase of the two-dimensional complex field U(x,y)is given by A(x,y) and φ(x,y), respectively. Note that, terms Amax (maximum of A(x,y)) and B = Amax/2 do not depend on the transversal coordinates (x,y). From the theory, if we set Amax=2, then B =1. Hence, the complex field U(x,y) can be obtained, in a simple manner, from the coherent sum of uniform waves Beiϑ(x,y) and Beiθ(x,y). In practice, this is accomplished with a common-path interferometer made up of a single phase element α(x,y), placed at the input plane of an imaging system. The single phase element is constructed by spatial multiplexing of the phase terms ϑ(x,y)
and θ(x,y) with the help of two-dimensional binary gratings (checkerboard patterns) M1(x,y) and M2(x,y) as follows
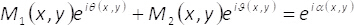 (4)
(4)
hence,
 (5)
(5)
These binary patterns fulfill the condition M1(x,y) + M2(x,y) = 1. Note that, the interference of uniform waves cannot happen if we do not mix the information contained in the phase elementα(x,y). In the present method, this is carried out by using a spatial filter able to block all diffraction orders but the zeroth one. In this way, after the filtering process at the Fourier plane, the spectrum H(u,v)= F{eiα(x,y)} of the encoded phase function is related to the spectrum of the complex field F{U(x,y)} by the expression
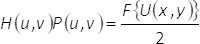 (6)
(6)
In Eq. (6), (u,v) denote coordinates in the frequency domain, P(u,v) holds for the spatial filter, whereas the Fourier transform of a given function Θ(x,y) is represented in the form F{Θ(x,y)}. From Eq. (6), it follows that, at the output plane of the imaging system, the retrieved complex field URET(x,y), (without considering constant factors), is given by the convolution of the magnified and spatially reversed complex field U(x,y) with the Fourier transform of the filter mask. That is:
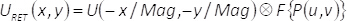 (7)
(7)
In Eq. (7), the convolution operation is denoted by the symbol  , and the term Mag represents the magnification of the imaging system. Hence, the amplitude and phase of U(x,y) is fully retrieved at the output plane, except for some loss of spatial resolution due to the convolution operation.
, and the term Mag represents the magnification of the imaging system. Hence, the amplitude and phase of U(x,y) is fully retrieved at the output plane, except for some loss of spatial resolution due to the convolution operation.
Protocol
1. Encoding the Complex Field into a Single Phase Element
- From the technical specifications of the SLM, find its spatial resolution (for instance 1920 pixels x 1800 pixels).
- Define and generate the desired amplitude A(x,y) and phase φ(x,y) patterns as digital images.
- Set the spatial resolution of abovementioned digital images equal to that of the SLM display.
- Set abovementioned digital images in gray level format.
- Set the minimum and maximum values of the amplitude and phase images from 0 to 255, and from -π/2 to π/2, respectively.
- Set Amax = 2 in equations 2 and 3, and computer-generate the phase patterns ϑ(x,y) and θ(x,y) from them.
- Computer generate the checkerboard patterns M1(x,y) and M2(x,y).
- Set the spatial resolution of these checkerboard patterns equal to that of the SLM display.
- To reduce the effect of pixel crosstalk, generate other pairs of checkerboard patterns M1(x,y) and M2(x,y) constructed with different pixel cells having an increased number of pixels (for instance: 2×2, 3×3, and 4×4 pixel cells, etc.).
CAUTION: When increasing the pixel cell, the total number of pixels of checkerboard patterns must be kept unchanged and equal to the spatial resolution of the SLM. Ensure that final number of pixels of all checkerboard patterns remains the same after modifying their pixel cells.
- Computer generate the single phase element α(x,y) from equation 5.
NOTE: See supplemental material named “MATLAB_code_1.m” for related tasks on step 1 of this protocol.
2. Reconstruction of the Complex Field
- Use a collimated, linear polarized, and spatially coherent laser beam as a light source.
- Use a phase-only SLM with at least 2π phase range.
- When necessary, use a proper beam expander to adjust the size of the beam to the size of the SLM display.
- When necessary, use an optical polarizer to set laser beam polarization to the horizontal direction. This is usually important for the proper operation of phase-only SLMs, which are typically designed to modulate the spatial phase of the electromagnetic field that oscillate in the horizontal direction, keeping unchanged its vertical components.
- In order to send a phase pattern to the SLM, follow standard communication protocols given by the SLM’s manufacturer to connect and control the SLM with the computer.
NOTE: Common protocol for this purpose includes the use of a calibration curve to transform the values in radians (due to mathematical operations with angles) into gray level ones, which the electronic control unit of the SLM will finally convert into voltage levels. Additionally, as the SLM is connected to computer as an external device with its own screen, an extension of the computer screen is usually necessary, as well as a proper program to send the corresponding gray level images to this extra screen. An example of these codes is also included as supplemental material (please, see MATLAB_code_2.m). - Implement an image optical system and put the display of the SLM in the input plane of this system.
- Use a refractive lens of a focal length f to construct a 2f x 2f optical image system (a 4f optical system is also valid for this task). In accordance with the expected output size of the complex field, beam width, wavelength of light, and the available physical space, employ lens/lenses with suited technical specifications (e.g., coating, size, focal length, etc.).
- To find the position of the output plane of the imaging system, send the phase pattern α(x,y) to the SLM and visually look for the recorded image (depending on the position of the camera) with the best spatial resolution.
CAUTION: In the case of low-size pixel cells (for instance, 1×1 pixel cells) and SLM displays with pixel widths of a few microns (for instance, 8 µm), only beam propagation can produce interference between encoded uniform waves, getting a reconstructed images without including the circular iris in the imaging system. Use low-size pixel cells to locate the position of the output plane. - Place a circular iris of variable diameter at the Fourier plane of the optical system and align its center with that of the laser beam focus.
- To adjust the size of the circular iris at the Fourier plane, send the phase pattern α(x,y) and visually look for the recorded image (depending on the diameter of the circular iris) with best spatial resolution.
CAUTION: In the case of long-size pixel cells (for instance, 4×4 pixel cells), the interference between encoded uniform waves is basically carried out with the spatial filter. Use long-size pixel cell to adjust the size of the circular iris. In this protocol, the terms low-size and long-size are referred to the number of pixels contained within a pixel cell. However, the abovementioned interference depends also on the pixel width. Employ SLMs with pixel widths equal or less than 8 µm.
- Send the gray level image corresponding to the phase element α(x,y) to the SLM.
- To minimize the crosstalk effect, look for the best pixel cell size which allow achieving the recorded image with the higher spatial resolution.
3. Measure the Reconstructed Complex Field
- Implement the polarization-based phase shifting technique8.
- Place and align the rotation angle of the first optical polarizer, located just before the SLM (see Figure 2). To set the rotation angle of the first polarizer, visually look for the maximum and minimal light transmittance in the CCD camera (placed at the output plane of the imaging system), depending on the rotation of the polarizer. Write down the two corresponding angles of the polarizer. Fix the final angle of the polarizer to that between the two previous-recorded angles.
- Place and align the rotation angle of the second optical polarizer, located after the Fourier plane of the imaging system (see Figure 2). To set the rotation angle of the second polarizer, visually look for the sharpest and most blurred images in the CCD camera (placed at the output plane of the imaging system) after sending the phase pattern α(x,y) to the SLM. Write down the two corresponding angles of the polarizer. Fix the final angle of the second polarizer to that between the previous-recorded angles.
- Record the interferograms.
- Keep the CCD camera at the output plane of the imaging system.
- To record the first interferogram, add a matrix of 0 radians to the phase element α(x,y) and send it to the SLM. Record corresponding image I1(x,y) with the CCD.
- To record the second interferogram, add a matrix of π/2 radians to the phase element α(x,y) and send it to the SLM. Record corresponding image I2(x,y) with the CCD camera.
- To record the third interferogram, add a matrix of π radians to the phase element α(x,y) and send it to the SLM. Record corresponding image I3(x,y) with the CCD camera.
- To record the fourth and last interferogram, add a matrix of 3π/2 radians to the phase element α(x,y) and send it to the SLM. Record corresponding image I4(x,y) with the CCD camera.
- Reconstruct the complex field.
NOTE: See supplemental material named “MATLAB_code_3.m” for related tasks on this point of the protocol.- Retrieve the amplitude of the complex field Aretrieved(x,y) by using the expression
 (8)
(8) - Retrieve the phase of the complex field φretrieved(x,y) by using the expression
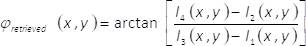 (9)
(9)
- Retrieve the amplitude of the complex field Aretrieved(x,y) by using the expression
Representative Results
The spatial resolution of the employed phase-only SLM is 1920 pixels x 1080 pixels, with a pixel pitch of 8 µm. The selected amplitude A(x,y) and phase φ(x,y) of the complex field are defined by two different gray level images corresponding to the well-known Lenna’s picture (amplitude pattern) and a young girl sticking out her tongue (phase pattern), respectively. In general, for both, the generation of necessary patterns, and the control of the SLM, Matlab codes are utilized. The spatial resolution of these images is set to be 1920 pixels x 1080 pixels. Then, equations 2 and 3 are used to determine the phase patterns ϑ(x,y) and θ(x,y) for Amax = 2. Note that, the numerical value given to Amax guaranties that term B = 1 and consequently, the complex field U(x,y) described by Eq. (1) can be understood as the sum of two uniform waves in the simplest form U(x,y) = eiϑ(x,y) + eiθ(x,y). Now, different pairs of binary checkerboard patterns M1(x,y) and M2(x,y) (for increased pixel cell sizes), but equal spatial resolution (1920 pixels x 1080 pixels), are computer generated. Particularly, checkerboard patterns made up of 1×1, 2×2, 3×3 and 4×4 pixel cells are digitally constructed by using a programed Matlab function. All abovementioned patterns A(x,y), φ(x,y), ϑ(x,y), θ(x,y), M1(x,y), and M2(x,y) are shown in parts A, B, C, D, E, and F of Figure 1, respectively. In parts E and F, and just to get a better visualization of the structure of checkerboard patterns, the constituent pixel cells are of 240 pixels x 240 pixels. From Eq. 5, a set of phase elements α(x,y) for each pair of previously-designed checkerboard patterns are digitally constructed.

Figure 1: Computer generated patterns associated with the introduced encoding method. (A) User-defined amplitude pattern of the complex field. (B) User-defined phase pattern of the complex field. (C) Phase pattern corresponding to the first uniform wave in equation 1. (D) Phase pattern corresponding to the second uniform wave in equation 1. (E) First checkerboard pattern following the sampling process described with equation 4. (F) Second checkerboard pattern following the sampling process described with equation 4. Please click here to view a larger version of this figure.
At this point, the expected complex field U(x,y) can be experimentally retrieved at the output plane of an imaging system, once the phase element α(x,y) is sent to the phase-only SLM and the interference between encoded uniform waves takes place. To perform this interference, a spatial filter (for instance, a circular iris) is adjusted in size to block all frequencies but the zeroth one at the Fourier plane of the imaging system (Figure 2).

Figure 2: Optical setup used to accomplish the encoding method. Imaging system composed of a spatial light modulator (SLM), beam splitter (BS), and single refractive lens (L) of focal length 200 mm. In the Fourier plane is included a hard iris, which is employed as a spatial filter (SF) to block all frequencies but the zero one. In addition, at the output plane of the imaging system is placed a camera (CCD) to record amplitude patterns, and interferograms. Only to measure the generated complex field by means of polarization-based phase shifting technique, a couple of optical polarizers (P) are properly located within the optical setup. Please click here to view a larger version of this figure.
As a light source, a Ti: Sapphire laser oscillator (working out of the mode locked condition to emit a quasi-monochromatic laser radiation of about 10 nm intensity full width at half maximum (FWHM) and centered at 800 nm) is employed. In addition, to fill almost all the active area of the SLM display (8.64 cm x 15.36 cm) with the laser beam, a commercial 5x telescope beam expander is used. The laser beam is sent (in normal incident) to the display of the SLM by means of a pellicle beam splitter. A refractive lens of focal length 100 mm is placed 200 mm after the SLM and aligned with respect to the optical axis of the laser beam reflected back from the SLM. To locate the position of the output plane of the imaging system, the image of A(x,y) recorded the CCD camera was found. This is done once the phase element α(x,y) (formed with 1×1 pixel cells) is sent to the SLM. Then, a circular iris is placed at the Fourier plane of the optical system, and aligned with respect to the focus of the laser beam. In addition, to adjust the size of the circular iris, its diameter is varied until better image reconstruction is achieved by visual inspection in the CCD camera. To this purpose, the phase element α(x,y) (digitally constructed with 4×4 pixel cells) was previously sent to the SLM. To minimize the effect of pixel crosstalk, the best phase element α(x,y) (depending on the pixel cell size) that allows achieving the image with higher spatial resolution in the CCD is found.
In order to corroborate that the desired complex field is reconstructed at the output plane of the imaging system, the already-mentioned polarization-based phase shifting technique is used to measure its amplitude and phase. To do that, a couple of polarizers p (one placed before the SLM, and another after the output plane of the imaging system) are properly aligned within the optical setup (see Figure 2), following the procedure described in steps 3.1.1 and 3.1.2 of the protocol. Then, the interferograms associated with the four-step phase shifting technique I1(x,y), I2(x,y), I3(x,y), and I4(x,y) are recorded with the CCD camera (already placed at the output plane of the imaging system). Here, it should be recalled that these four interferograms are recorded with the camera after the addition of 0, π/2, π, and 3π/2 to the phase element α(x,y) (see steps 3.2.2 – 3.2.5 of the protocol for details). Finally, using equations 8 and 9, the amplitude and phase of the reconstructed complex field can be retrieved. For this experiment, the results are shown in Figure 3.

Figure 3: Representative experimental results under quasi-monochromatic illumination. (A) User-defined amplitude pattern of the complex field. (B) User-defined phase pattern of the complex field. (C) Interferograms associated with the polarization-based phase shifting technique developed in four steps and obtained after adding 0, π/2, π, and 3π/2 to the phase element α(x,y). (D) Retrieved experimental amplitude pattern. (E) Retrieved experimental phase pattern. Please click here to view a larger version of this figure.
Supplemental Materials. Please click here to download the files.
Discussion
In this protocol, practical parameters as the pixel width of the phase-only SLM or the number of pixels contained within pixel cells of a computer-generated pattern are key points to successfully implement the encoding method. In steps 1.2, 1.3, and 1.4 of the protocol, the shorter the pixel width, the better the spatial resolution of the retrieved amplitude and phase patterns. In addition, as the codification into the SLM of abrupt pixel-to-pixel phase modulations can originate unexpected phase responses (pixel crosstalk), the construction of checkerboard patterns (as described in step 1.3) should be linked to the increment of the number of pixels within pixel cells. The main reason to do that is to mitigate the effects of pixel crosstalk on the retrieved amplitude and phase patterns. However, when increasing the number of pixels within the pixel cells, the spatial resolution of the recorded complex field patterns Aretrieved(x,y) and φretrieved(x,y) is decreased. Hence, having high spatial resolution SLMs with low pixel widths allows reducing possible crosstalk effects, without losing significant spatial resolution in the retrieved amplitude and phase patterns.
Furthermore, in step 1.2.3 of the protocol, the phase of the complex field is defined from – π/2 to π/2. The main reason for setting such phase range is to generate a phase element α(x,y) ranging from -π to π, which can be implemented into a SLM with 2π of phase range. However, if the phase range of the available SLM is greater than 2π, the phase of the complex field could be defined within an extended range (for instance: for φ(x,y) ranging from -π to π, the phase element α(x,y) may range from -3π/2 to 3π/2, and consequently the phase range of the SLM must be, at least, 3π).
The characteristics of the laser beam could also influence the results of the encoding method. Pay special attention to the steps 2.1-2.4, setting the right polarization direction, collimation, and transversal size of the laser beam before following the remaining steps of the protocol. Furthermore, as phase-only SLMs are basically diffractive-dependent optical devices based on the interference phenomenon, it is necessary to use laser beams with high/good spatial coherence.
On the other hand, instead of quasi-monochromatic, ultrashort pulsed illumination also allows obtaining good results. In this case, the different spectral components of the pulse are phase modulated (in a very similar manner) just with the single phase element α(x,y). Here, to show the effect of a broadband light source on the encoding method, we repeat all steps of the protocol, but this time for pulsed radiation (an ultrashort pulse of about 12 fs FWHM, centered at 800 nm, spectral bandwidth of 100 nm FWHM, emitted by a mode-locked Ti:Sapphire laser from the femtolaser, at a 75 MHz repetition rate). The results are shown in Figure 4. Note that, due to the mix of the different spectral components of the pulse, the retrieved patterns are very close to the expected ones.

Figure 4: Representative experimental results under ultrashort pulsed illumination. (A) User-defined amplitude pattern of the complex field. (B) User-defined phase pattern of the complex field. (C) Interferograms associated with the polarization-based phase shifting technique developed in four steps and obtained after adding 0, π/2, π, and 3π/2 to the phase element α(x,y). (D) Retrieved experimental amplitude pattern. (E) Retrieved experimental phase pattern. Please click here to view a larger version of this figure.
Laser beams are intrinsically complex fields, so in most potential applications one should be able to modify their amplitude and phase, simultaneously. The present method allows to do that by means of a single phase element (implemented or not into a phase-only SLM). We believe that, in a near future, this method could be employed, for instance in the illumination path of microscopes9,10 for simultaneous linear and non-linear excitation of different zones of biological samples, or in parallel micro-processing11,12 of materials. In both applications the role of amplitude modulation is apparent, meanwhile phase modulation can be utilized, at the same time, for compensation of optical aberrations at the sample/processing plane. Finally, it should be mentioned that the encoding method described with the present protocol is not limited to the utilization of SLMs. Fixed phase elements α(x,y) constructed with other techniques (for instance: photolithographic techniques) can be a different, but equally valid option to implement this protocol.
Açıklamalar
The authors have nothing to disclose.
Acknowledgements
This research was supported by Generalitat Valenciana (PROMETEO 2016-079), Universitat Jaume I (UJI) (UJIB2016-19); and Ministerio de Economía y Competitividad (MINECO) (FIS2016-75618-R). The authors are very grateful to the SCIC of the Universitat Jaume I for the use of the femtosecond laser.
Materials
| Achromatic Doublet | THORLABS | AC254-100-B-ML | Lens Diameter 25.4 mm, focal length 100 mm |
| Achromatic Galilean Beam Expander | THORLABS | GBE05-A | AR Coated: 400 – 650 nm |
| Basler camera | BASLER | avA1600-50gm GigE camera | sensor size 8.8 mm x 6.6 mm, pizel size 5.5 microns |
| Mounted Zero-Aperture Iris | THORLABS | ID12Z/M | Max Aperture 12 mm |
| Pellicle Beamsplitter | THORLABS | CM1-BP145B2 | 45:55 (R:T), Coating: 700 – 900 nm |
| PLUTO Spatial Light Modulator | HOLOEYE Photonics AG | NIR-II | Phase Only Spatial Light Modulator (Optimized for 700 -1000 nm) |
| Two thin film laser polarizers | EKSMA OPTICS | 420-0526M | material BK7, diameter 50 mm, wavelength 780-820 nm |
Referanslar
- Hsueh, C. K., Sawchuk, A. A. Computer-generated double-phase holograms. Applied Optics. 17 (24), 3874-3883 (1978).
- Arrizón, V. Complex modulation with a twisted-nematic liquid-crystal spatial light modulator: double-pixel approach. Optics Letters. 28 (15), 1359-1361 (2003).
- Arrizón, V., Ruiz, U., Carrada, R., González, L. A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. Journal of the Optical Society of America A. 24 (11), (2007).
- Shibukawa, A., Okamoto, A., Takabayashi, M., Tomita, A. Spatial cross modulation method using a random diffuser and phase-only spatial light modulator for constructing arbitrary complex fields. Optics Express. 22 (4), 3968-3982 (2014).
- Martínez-Fuentes, J. L., Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Optics Express. 26 (5), 5875-5893 (2018).
- Clark, T. W., Offer, R. F., Franke-Arnold, S., Arnold, A. S., Radwell, N. Comparison of beam generation techniques using a phase only spatial light modulator. Optics Express. 24 (6), 6249-6264 (2016).
- Mendoza-Yero, O., Mínguez-Vega, G., Lancis, J. Encoding complex fields by using a phase-only optical element. Optics Letters. 39 (7), 1740-1743 (2014).
- Yamaguchi, I., Zhang, T. Phase-shifting digital holography. Optics Letters. 22 (16), 1268-1270 (1997).
- Shao, Y., et al. Addressable multiregional and multifocal multiphoton microscopy based on a spatial light modulator. Journal of Biomedical Optics. 17 (3), 030505 (2012).
- Mendoza-Yero, O., Carbonell-Leal, M., Mínguez-Vega, G., Lancis, J. Generation of multifocal irradiance patterns by using complex Fresnel holograms. Optics Letters. 43 (5), 1167-1170 (2018).
- Kuang, Z., et al. Diffractive Multi-beam Ultra-fast Laser Micro-processing Using a Spatial Light Modulator (Invited Paper). Chinese Journal of Lasers. 36 (12), 3093-3115 (2009).
- Kuang, Z., et al. High throughput diffractive multi-beam femtosecond laser processing using a spatial light modulator. Applied Surface Science. 255, 2284-2289 (2008).

