Half-life of a Reaction

The half-life of a reaction (t_1/2) is the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed. For example, during the decomposition of hydrogen peroxide, during the first half-life (from 0.00 hours to 6.00 hours), the concentration of H₂O₂ decreases from 1.000 M to 0.500 M. During the second half-life (from 6.00 hours to 12.00 hours), the concentration decreases from 0.500 M to 0.250 M, while during the third half-life, it falls from 0.250 M to 0.125 M. Hence, during each successive period of 6.00 hours, the concentration of H₂O₂ decreases by half.

The half-life of a first-order reaction is independent of the concentration of the reactant. However, half-lives of reactions with other orders depend on the concentrations of the reactants.

Half-life of First-order Reactions

An equation relating the half-life of a first-order reaction to its rate constant may be derived from its integrated rate law:

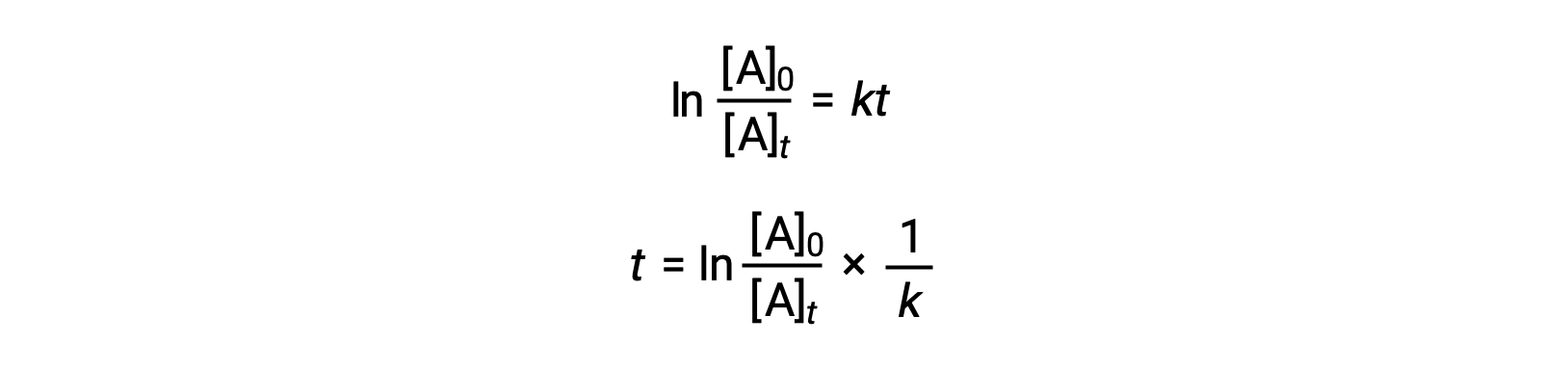
According to the definition of half-life, at time t_1/2, the concentration of the reactant A is one-half of its initial concentration. Therefore; t = t_1/2  and [A]_t = ½ [A]₀.

Substituting these terms into the rearranged integrated rate law and simplifying yields the equation for half-life:

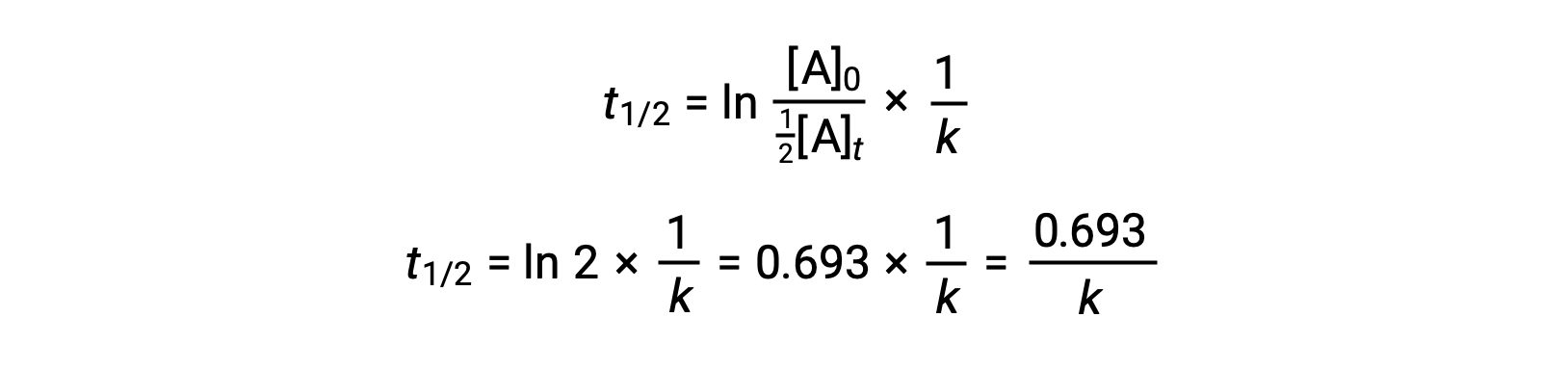
This half-life equation describes an expected inverse relationship between the half-life of the reaction and its rate constant, k. Faster reactions exhibit larger rate constants and correspondingly shorter half-lives, while slower reactions exhibit smaller rate constants and longer half-lives.

Half-life of Second-order Reactions

Following the same approach as for first-order reactions, an equation relating the half-life of a second-order reaction to its rate constant and initial concentration may be derived from its integrated rate law: 

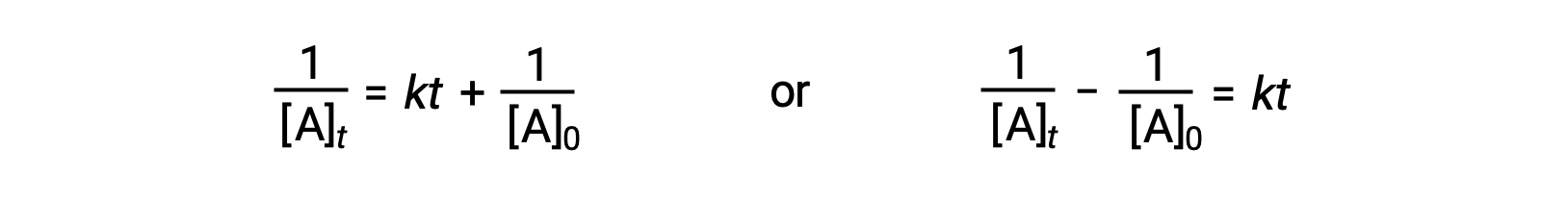
On substituting t = t_1/2  and [A]_t = ½[A]₀, the integrated rate law is simplified:

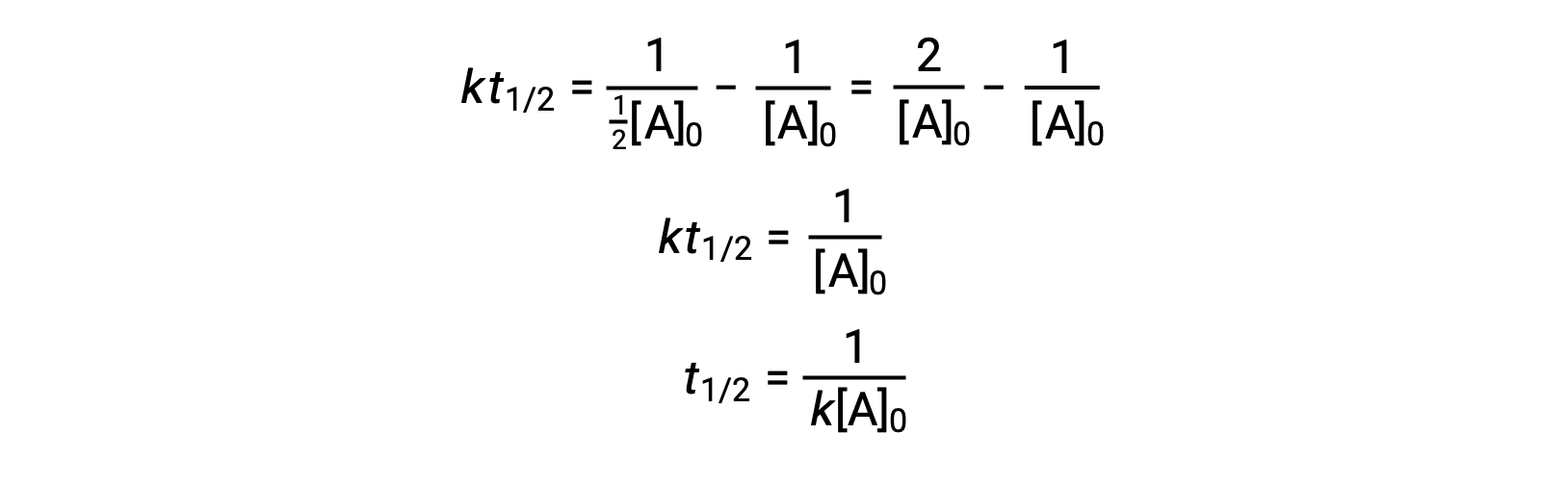
For a second-order reaction, t_1/2 is inversely proportional to the concentration of the reactant, and the half-life increases as the reaction proceeds because the concentration of the reactant decreases. Unlike with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.

Half-life of Zero-order Reactions

An equation for zero-order half-life may be also be derived from its integrated rate law:   

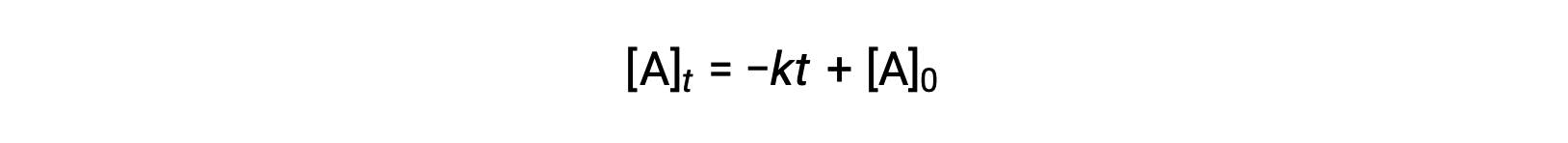
Substituting t = t_1/2  and  [A]_t = ½ [A]₀, in the zero-order integrated rate law yields:

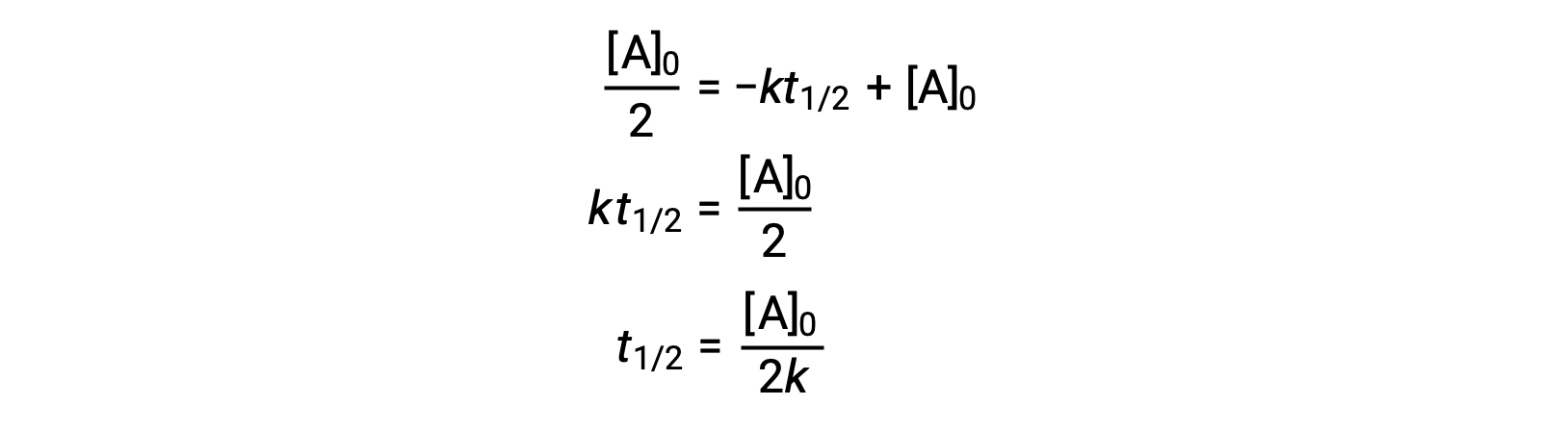
The half-life for a zero-order reaction is inversely proportional to its rate constant. However, the half-life of a zero-order reaction increases as the initial concentration increases.

This text is adapted from Openstax, Chemistry 2e, Section 12.4: Integrated Rate Laws.