25.10:
Potential Due to a Polarized Object
216 Views
•
•
A neutral atom consists of a positively charged nucleus surrounded by a negatively charged electron cloud. When placed in an external electric field, the external electric force pulls the electrons and nucleus apart, opposite to the intrinsic attraction between the nucleus and the electrons. The opposing forces balance each other with a slight shift between the center of masses of the nucleus and the electron cloud, resulting in a polarized atom. On the other hand, a few molecules, like water, inherently have this separation. For such molecules, when kept in a uniform electric field, the forces exerted on the positive and negative sides cancel each other; however, a net torque exists. In both cases, the dipoles point along the electric field direction, leading to polarization, which is given by the dipole moment per unit volume.
Consider a cylindrical dielectric material. In a string of aligned dipoles along the length of the cylinder, with a constant dipole moment, the equal and opposite charges in the adjacent dipoles cancel each other. Hence, there are net charges at both ends of the cylinder called surface-bound charges. These are called bound charges as they are still bound to the specific atoms or molecules and are not free to move in the dielectric. The surface-bound charge density is the charge per unit area on either surface.
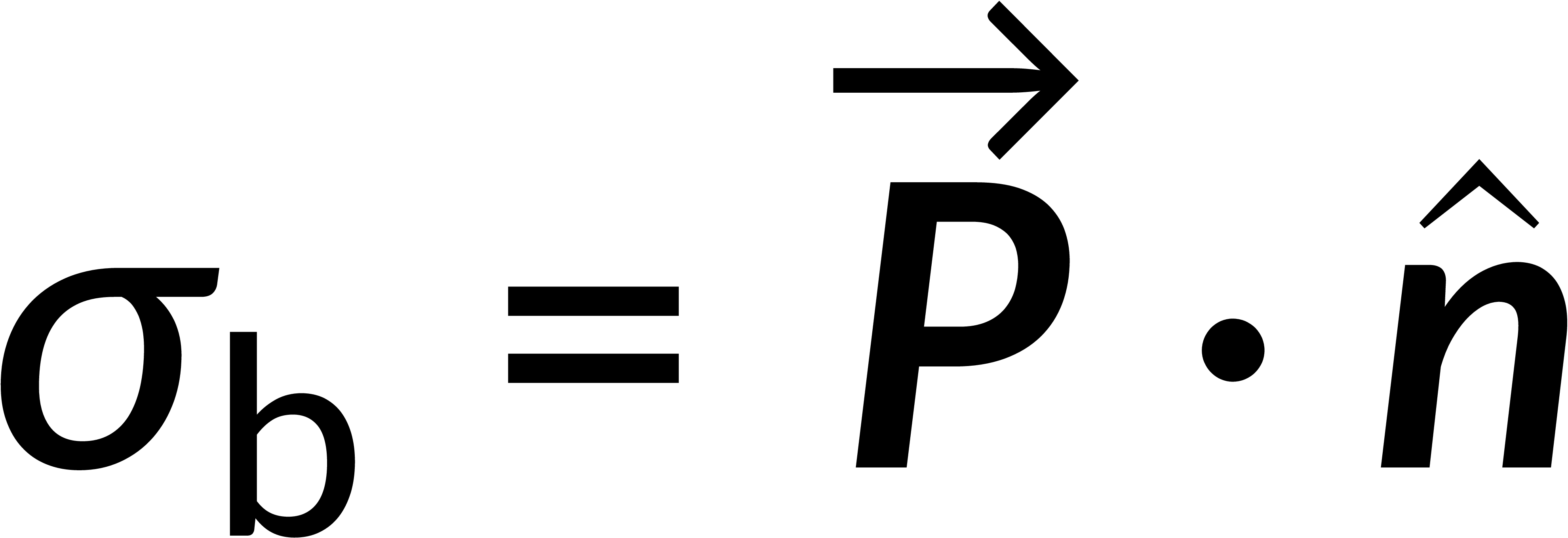
Suppose the electric field and polarization are diverging in nature. In that case, the alignment of the dipoles accumulates charges inside the polarized dielectric, leading to volume-bound charges that are equal and opposite to the surface-bound charges.
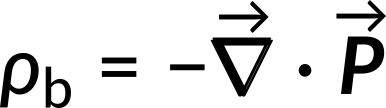
Recalling the potential due to a dipole, the potential created by the polarized dielectric at any field point can be measured by knowing the potentials due to these surface-bound and volume-bound charges.

