A Rapid Laser Probing Method Facilitates the Non-invasive and Contact-free Determination of Leaf Thermal Properties
Summary
A method was developed to determine the specific heat capacity and thermal conductivity of leaf tissue by non-invasive, contact-free near infrared laser probing, which requires less than 1 min per sample.
Abstract
Plants can produce valuable substances such as secondary metabolites and recombinant proteins. The purification of the latter from plant biomass can be streamlined by heat treatment (blanching). A blanching apparatus can be designed more precisely if the thermal properties of the leaves are known in detail, i.e., the specific heat capacity and thermal conductivity. The measurement of these properties is time consuming and labor intensive, and usually requires invasive methods that contact the sample directly. This can reduce the product yield and may be incompatible with containment requirements, e.g., in the context of good manufacturing practice. To address these issues, a non-invasive, contact-free method was developed that determines the specific heat capacity and thermal conductivity of an intact plant leaf in about one minute. The method involves the application of a short laser pulse of defined length and intensity to a small area of the leaf sample, causing a temperature increase that is measured using a near infrared sensor. The temperature increase is combined with known leaf properties (thickness and density) to determine the specific heat capacity. The thermal conductivity is then calculated based on the profile of the subsequent temperature decline, taking thermal radiation and convective heat transfer into account. The associated calculations and critical aspects of sample handling are discussed.
Introduction
The large-scale processing of biological materials often requires heat-treatment steps such as pasteurization. The equipment for such processes can be designed more precisely if the thermal properties of the biological materials are well characterized, including the specific heat capacity (cp,s) and thermal conductivity (λ). These parameters can be determined easily for liquids, suspensions and homogenates by calorimetry 1. However, measuring such parameters in solid samples can be labor intensive, and often requires direct contact with the sample or even its destruction 2. For example, photothermal techniques require direct contact between the sample and detector 3. Such limitations are acceptable during food processing, but are incompatible with highly regulated processes such as the production of biopharmaceutical proteins in plants in the context of good manufacturing practice 4. In such a context, repeated (e.g., weekly) monitoring of thermal properties may be required during a seven-week growth period for individual plants as a quality control tool. If such a monitoring would require and consume a leaf for each measurement, there would be no biomass left to process at the time of harvest.
Additionally, using only leaf parts instead would cause wounding to the plant and increase the risk of necrosis or pathogen infection, again diminishing the process yield. The likelihood of pathogen infection may also increase if a method with direct contact to the sample would be used, inducing the risk that an entire batch of plants can be infected through contact with a contaminated sensor device. Similar aspects have to be considered for the monitoring of plant stresses like drought, e.g., in an ecophysiological context. For example, water loss is often monitored by a change in the fresh biomass, which requires an invasive treatment of the plants under investigation 5, e.g., dissecting a leaf. Instead, determining the specific heat capacity, which depends on the water content of a sample, in a non-invasive manner as describe here, can be used as a surrogate parameter for the hydration status of plants. In both scenarios (pharmaceutical production and ecophysiology), artificial stresses induced by destructive or invasive measurement techniques would be deleterious as they can distort the experimental data. Therefore, previously reported flash methods 6 or the placement of samples between silver plates 7 are unsuitable for such processes and experiments because they either require direct contact to the sample or are destructive. The parameters cp,s and λ must be determined in order to design the process equipment for a blanching step that can simplify product purification and thus reduce manufacturing costs 8-10. Both cp,s and λ can now be rapidly determined by contact-free non-destructive near infrared (NIR) laser probing in a consistent and reproducible manner 11 and this new method will be explained in detail below. The results obtained with this method were successfully used to simulate heat transfer in tobacco leaves 12, allowing the design of appropriate processing equipment and the selection of corresponding parameters such as the blanching temperature.
The method is easy to set up (Figure 1) and has two phases, measurement and analysis, each of which comprises two major steps. In the measurement phase, a leaf sample is first locally heated by a short laser pulse and the maximum sample temperature is recorded. The temperature profile of the sample is then recorded for a duration of 50 s. In the analysis phase, leaf properties such as density (easily and accurately determined by pycnometric measurement) are combined with the maximum sample temperature to calculate cp,s. In the second step, the leaf temperature profile is used as the input for an energy balance equation, taking conduction, convection and radiation into account, to calculate λ.
Detailed step-by-step instructions are provided in the protocol section, expanding on the contents of the accompanying video. Typical measurements are then shown in the results section. Finally, the benefits and limitations of the method are highlighted in the discussion section along with potential improvements and further applications.
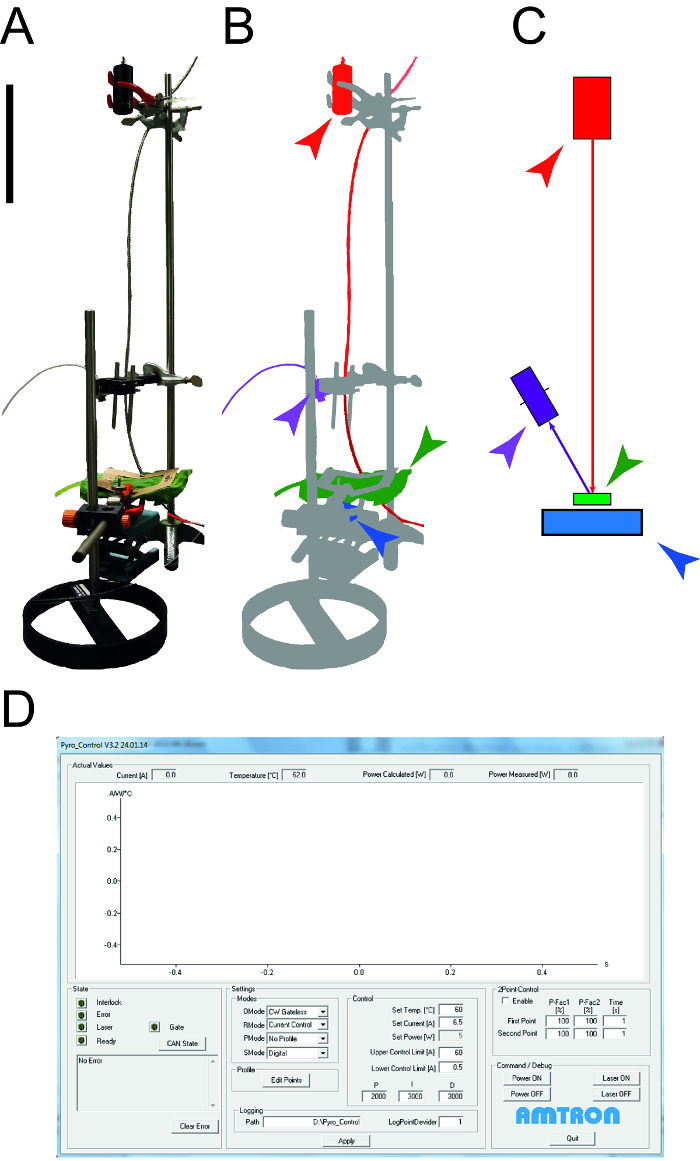
Figure 1: Apparatus used to determine leaf thermal properties. A. Photograph of the measurement apparatus used to determine the specific heat capacity and thermal conductivity of leaves. The peripheral devices (computers, oscilloscope) are not shown. B. Schematic representation of the measurement apparatus. The laser and connected equipment are highlighted in red, the NIR detector for temperature measurement is shown in purple, the leaf sample is green and the photodiode power sensor is blue. C. Drawing of the elements of the measurement setup with the same color code as in B. The size bar indicates 0.1 m. D. Screenshot illustrating the typical elements of the laser control software. Please click here to view a larger version of this figure.
Protocol
1. Plant Cultivation and Sample Preparation
- Flush each mineral wool block with 1-2 L of deionized water and subsequently with 1 L of 0.1% [m/v] fertilizer solution. Place one tobacco (Nicotiana tabacum or N. benthamiana) seed in each block and gently flush with 0.25 L of fertilizer solution without washing away the seed.
- Cultivate the plants for 7 weeks in a greenhouse or phytotron with 70% relative humidity, a 16-h photoperiod (180 µmol s−1 m−2; λ = 400-700 nm) and a 25/22 °C light/dark temperature regime.
- Move the plants to the measurement apparatus. If the plants are immobile, harvest single leaves for the measurement of thermal properties.
2. Determine Leaf Thickness and Density
- Determine the leaf thickness
- Prepare a 2% [m/v] agarose solution in phosphate-buffered saline (PBS) and autoclave it. Let the solution cool down to 40 °C and embed a leaf sample placed in a Petri dish. Solidify the agarose by placing the Petri dish in a refrigerator at 4 °C for 30 min.
- Cut the agarose block into 200-µm slices using a vibratome with a razor blade cutting angle of 15°. Use a cutting velocity of 1.0 mm s-1 and an amplitude of 0.5 mm.
- Mount five transversal leaf sections on a glass slide using cyanoacrylate as a fixative. Determine the leaf thickness under a microscope with a 20× objective and an eyepiece with 10× magnification, using the measurement tools built into the microscope software according to the manufacturer's instructions.
- Determine the leaf thicknesses in sample areas without veins.
- Alternatively, determine the leaf thickness with a dial-gauge at a vein-free area of the leaf blade. Make sure the dial-gauge is held perpendicular to the plane of the leaf blade.
CAUTION: Cyanocrylate is a skin irritant and may also glue fingers together if not handled with care.
- Determine the leaf density
- Determine the empty mass (m0) of a dry pycnometer, then fill it with water and determine the mass again (m1). Dry the pycnometer completely, place a leaf inside and determine the mass (m2) once more. With the leaf inside, carefully fill up the pycnometer with water and determine the mass (m3).
- Calculate the leaf density (Ps) using Equation 1.
Equation 1: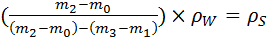
3. Determine the Spectral Transmission and Reflection of Leaves
- Place a leaf in the sample chamber of a UV/VIS spectrophotometer by fixing it between sample-holding clamps. For transmission measurements, place the leaf in front of the detector. For reflection measurements place the leaf at the rear of the detection chamber.
- Launch the spectrophotometer control software. Select a spectrum from 900 nm to 1600 nm. Start a new scan and record the values for transmission (µT) and reflection (µR) displayed by the UV/VIS spectrophotometer software, based on the spectral curve.
- Perform all measurements with at least three biological replicates. Increase the number of biological replicates to five or more if a heterogeneous sample quality can be expected, i.e., variation in leaf surface morphology and thickness.
- Calculate the power for transmission (PT) and reflection (PR) by multiplying the measured µT or µR values by the measured laser power PLaser according to Equations 2 and 3.
Equation 2: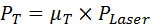
Equation 3: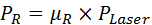
NOTE: The transmission can be also determined with a photodiode sensor during the measurement (see 6.3).
4. Set up the Measurement Apparatus
- Mount a fiber-coupled single-bar NIR diode laser (wavelength = 1,550 nm) into a 25.4-mm diameter cone on a stainless-steel holder. Connect a controller to set the output power (PLaser) of the NIR laser to 4-6 W.
- Place a bi-convex lens with a focal length of 25.4 mm at the end of the cone to adjust the beam width to 13 mm.
- Place a photodiode power sensor 354 mm below the bottom of the lens. Then attenuate the photodiode by placing a neutral density filter with an optical density of 1.0 and a 22-mm ceramic layer above the sensor.
- Connect the photodiode power sensor to an oscilloscope using a coaxial cable.
- Connect a 10 × 10 cm frame which has a 6 × 6 cm sample exposure area with the scaffold of the measurement setup at a height of 308 mm below the lens (Figure 1). Fix the leaf position in space by mounting it into the 10 × 10 cm frame.
- Connect a NIR detector to a personal computer using a universal serial bus (USB) cable and install the interface software for the detector.
- Place the detector at a 45° angle to the laser beam 135 mm above the ceramic layer. Align the measurement area of the detector to the laser spot on the sample by varying the sensor position and angle until the maximum temperature signal is observed.
- Use the laser control interface software to adjust the output laser power to 5 W and the duration of the laser pulse to 0.5 s. Select the "Current control" command in the control options window below the graphical representation of the laser power and adjust the laser power by typing "5" into the "Power [W]" field. Adjust the laser pulse duration by typing "0.5" into the "Time [s]" field.
- To determine the absolute laser power for each set of experiments, replace the photodiode power sensor with a thermal surface absorber power sensor at the end of each set of experiments and measure the laser output power for 20 s without a sample.
5. Prepare the Leaf Samples
- Use intact and undamaged leaves for the measurements.
- If relevant for the investigation, mimic typical leaf damage types by piercing the leaf with a scalpel, rubbing the leaf between latex gloves, exposing the leaf to an open flame or a laser beam for 2-3 s, or use other techniques to simulate other types of damage.
- Carefully but quickly mount the leaf sample between sample-holding clamps.
6. Take the Temperature Measurements
- Avoid direct contact between the leaf and the ceramic attenuator placed above the photodiode sensor to prevent artificial heat transfer that interferes with the calculation of cp,s and λ (see section 9).
- Use the temperature measurement software to collect the temperature profile of the leaf sample for a total of 60 s via the NIR detector. First, record the temperature baseline for 10 s, then activate the laser for 0.5 s and continue data collection for 49.5 s.
- Start a measurement by clicking "Measurement" and then "New Measurement". Afterwards click the green arrow above the graphical representation of the thermal profile. Save the temperature profile by clicking on the "Save" icon (a stylized disk) above the graphical representation of the profile.
- Confirm the transmitted laser power using the photodiode power sensor by calculating the difference in signal for measurements with and without a leaf sample using an oscilloscope connected to the photodiode power sensor via a coaxial cable (Figure 2).
- Determine the height of the two flanks (f1,S and f2,S) in the voltage profile acquired with the oscilloscope.
- Repeat the measurement without a leaf sample as a reference (f1,0 and f2,0). Calculate transmission µT as the ratio of these measurements according to Equation 4 (see also Figure 2).
Equation 4: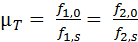
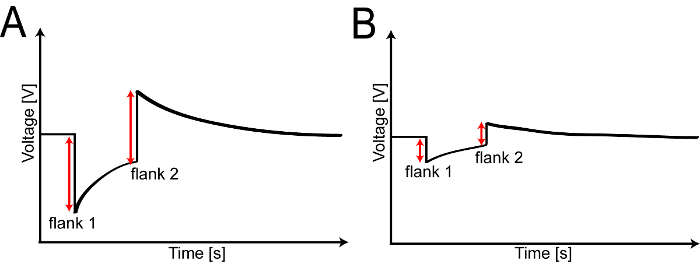
Figure 2: Measuring leaf transmission using a photodiode power sensor. A. Typical voltage profile for a reference experiment without a leaf sample visualized using an oscilloscope. B. Voltage profile with a leaf sample mounted in the apparatus. In both cases, the transmitted laser power is proportional to each of the two flanks. Please click here to view a larger version of this figure.
7. Calculate the Specific Heat Capacity of the Leaf Sample
- Calculate the maximum temperature difference ΔT [K] during the laser pulse by subtracting the room temperature T0 [K] from the maximum leaf temperature Tmax [K] (Equation 5).
Equation 5: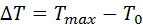
- Calculate the energy absorbed by a leaf (ES [J]) based on the effective laser power and laser pulse duration (Equation 6), where PR [W] is the reflected laser power and PT [W] is the transmitted laser power.
Equation 6: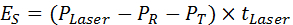
- Calculate the mass of the heated leaf area (mS [kg]) using Equation 7, where dS [m] is the leaf thickness according to 2.1), rLaser [m] is the radius of the laser spot, VS [m3] is the heated leaf volume, and ρS [kg m-3] is the leaf density according to 2.2).
Equation 7: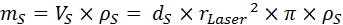
- Calculate cp,s[J kg-1 K-1] according to Equation 8 by dividing the absorbed energy ES by the product of the heated leaf area mass mS and maximum temperature difference ΔT.
Equation 8: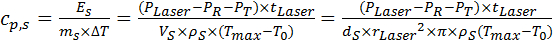
8. Prepare the Temperature Profile Data for Thermal Conductivity Calculations
- Use the "Export" command of the NIR sensor control software to export the time and temperature raw data as a *.dat file and open the file in a spreadsheet processor.
- Apply 1:100 data reduction, e.g., using an "IF(MOD(Value;100)=0;"x";"0")" command, resulting in a data density of one data point per 0.1 s.
- Calculate the average baseline temperature TB [°C] for each temperature profile over the initial 10 s of a measurement, during which the laser was still off. Then, calculate the difference between TB and the actual ambient temperature T0 [°C].
- Use this difference to individually normalize each profile by shifting it towards T0 (y-normalization), e.g., if TB–T0 = 2.0 K, then subtract 2.0 K from each temperature value in the temperature profile (Figure 3A).
- Normalize the time coordinate of each temperature profile (x-normalization) by deleting every data point before the maximum sample temperature (Tmax) and assign new time values starting with t = 0 for Tmax (Figure 3B).
- Screen each profile for sudden temperature shifts, i.e., temperature differences that are more than three times the baseline noise level, which is typically 3 × 0.31 K ≈ 1.0 K. Remove these regions from the data set because they correspond to measurement artifacts (Figure 3C).
- Fit an exponential decay function (Equation 9) to the data using a spreadsheet processor, where Tt [K] is the fitted leaf sample temperature at time t [s], T0 is the ambient temperature, A [K] is the amplitude and t1 [s] the decay constant (Figure 3D).
Equation 9: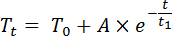
- Use the fitted function to calculate the temperature decline in the leaf sample from 0-80 s after the laser pulse.
- Transform the temperature data measured in [°C] to the [K] scale by adding a value of 273.15 to each temperature data point (Figure 3E).
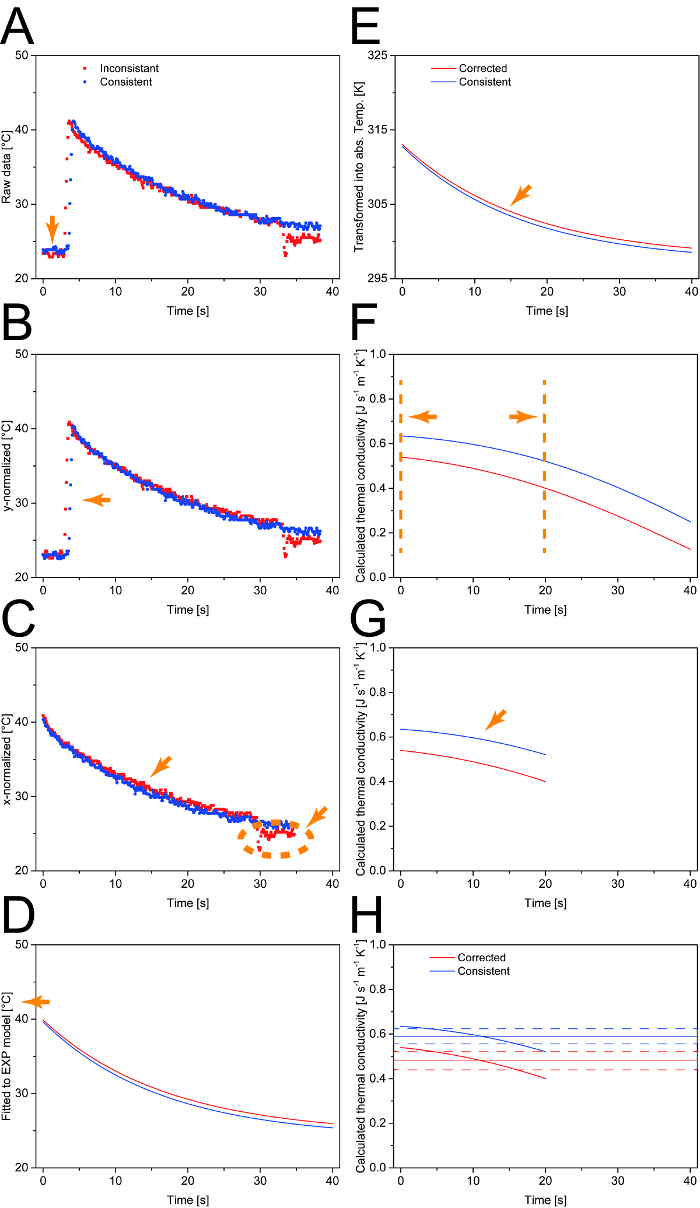
Figure 3: Data processing scheme for the calculation of λ. A. After data reduction, the temperature profiles are normalized to the ambient temperature. B. Next, all data points before the maximum sample temperature (Tmax) are removed. C. Measurement artifacts (shown in the "inconsistent" data set) are identified based on temperature shifts larger than three times the baseline noise and removed from the dataset prior to fitting to an exponential function. D. The Celsius temperature scale is converted into the Kelvin scale. E. For each time interval, λ is calculated based on the temperature profile. F. A window of 20 s is defined in which a relevant temperature change can be observed. G. Based on the selected time window, the average and standard deviation are calculated for λ. H. Representative results for two different N. tabacum leaf samples. Orange arrows and lines indicate the effect of the corresponding processing step on the presented data. Please click here to view a larger version of this figure.
9. Calculation of the Thermal Conductivity of the Leaf Sample
- Calculate the temperature difference between the leaf sample and the environment for each 0.1-s interval according to Equation 10, where ΔTx [K] is the temperature difference, Tt [°C] is the fitted leaf sample temperature and T0 [°C] the ambient temperature (Figure 3E).
Equation 10:
- Assume that the decline in temperature is due to the combined effect of convective heat transfer, thermal radiation and thermal conduction. Use the corresponding energy balance (Equation 11) as a basis for the calculation of λ, where ΔETemp[J] is the difference in the thermal energy of the sample at two consecutive time points, ΔErad [J] is the energy difference due to thermal radiation, ΔEconv [J] is the energy difference due to convective heat transfer, and ΔEcond [J] is the energy difference due to thermal conduction.
Equation 11: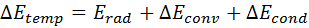
- Substitute the general terms in the energy balance with the actual physical properties yielding Equation 12, where ΔTt [K] is the difference in the fitted leaf sample temperature, ε the unitless emissivity, σ [kg s-3 K-4] the Stefan-Boltzmann constant, Arad [m2] the area of thermal radiation, h [J s-1 m-2 K-1] the convective heat transfer coefficient, Aconv [m2] the area of convective heat transfer, Acond [m2] the area of thermal conduction and l [m] the characteristic length.
Equation 12:
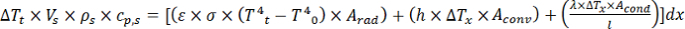
- Calculate the characteristic length l based on the correlation: l = V/A.
- Use the heated sample volume VS and the cross-sectional area of the leaf sample to calculate A [m2]. The cross-sectional leaf area corresponds to Acond according to Equation 13, where Acond is the area where conduction occurs, rLaser is the radius of the laser spot and ds is the leaf thickness.
Equation 13: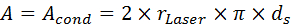
- Calculate Arad and Aconv according to Equation 14, where ALaser is the area of the laser spot.
Equation 14: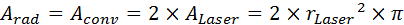
- Substitute Equations 9, 12 and 13 into Equation 11 and resolve the latter for λ, yielding Equation 15 where tLaser is the laser pulse duration [s].
Equation 15:

- Assume a value of 0.94 for ε and calculate λ for each 0.1-s time interval over the first 20 s of the temperature profile. Average the 200 values for λ obtained in this way and calculate the standard deviation (Figure 3F − H).
Representative Results
Measurement of Leaf Properties
Using the above microscopic method, a leaf thickness of 0.22-0.29 × 10−3 m was determined for both N. tabacum (0.25±0.04 × 10−3 m, n=33) and N. benthamiana (0.26±0.02 × 10−3 m, n=24), which is well within the 0.20-0.33 × 10−3 m range previously reported for the leaves of various plant species 3. Determining the thickness with a dial-gauge yielded values of ~0.28 × 10−3 m (n=10), which was within one standard deviation of the results from the microscopic measurement. Thus, the dial-gauge measurement may be preferred over the microscopic method for thickness determination in routine applications as it was easier to apply and the results for cp,s and ʎ deviated less than 10% from the more labor intensive technique. The density of N. tabacum and N. benthamiana leaves was 750±10 kg m−3 (n=20), which matches the 631-918 kg m−3 range previously reported for leaves in other species 3.
Calculation of the Specific Heat Capacity
Temperature profiles collected for Nicotiana species showed a rapid increase over the time of the laser pulse until the maximum temperature (Tmax) was reached within less than 1 s. After the pulse, the temperature decreased exponentially until it reached ambient temperature (T0) (Figure 3A−E). The specific heat capacity (cp,s) was calculated according to Equation 8 yielding values of 3661 ± 323 J kg-1 K-1 for N. tabacum and 2,252 ± 285 J kg-1 K-1 for N. benthamiana. Two cultivation settings and durations were used for each species (see section 1.2) but this did not affect cp,s (Figure 4). However, the cp,s values decreased linearly from the old (bottom) to young (top) leaves (R2 = 0.85) in the case of N. tabacum (Figure 4A), which correlated to the water content [g g-1 biomass] that had been determined as the difference of wet biomass at the time of harvest and the mass after 72 h incubation at 60 °C 11. This correlation between water content and specific heat capacity was in agreement with previous observations by other authors 13. An inverse correlation was observed for N. benthamiana (R2 = 0.79), where the difference between the specific heat capacities of leaves of different degrees of maturity (bottom = old; top = young) were only 13% compared to 21% for N. tabacum. This difference may originate in the fact that the water content in leaves of N. benthamiana is almost constant over the different degrees of leaf maturation 11. A sensitivity analysis revealed that differences in cp,s were proportional to fluctuations in the measurement parameters in Equation 8. The effect of the reflected and transmitted laser power was sub-proportional, because these parameters were not individual factors in Equation 7. Accordingly, the effect of errors in these two parameters was smaller than those caused by fluctuations in the laser power or ambient temperature. In general, the measurement was considered to be robust because all parameters involved in the calculation of cp,s had a coefficient variation of less than 10% (Figure 4C and D).
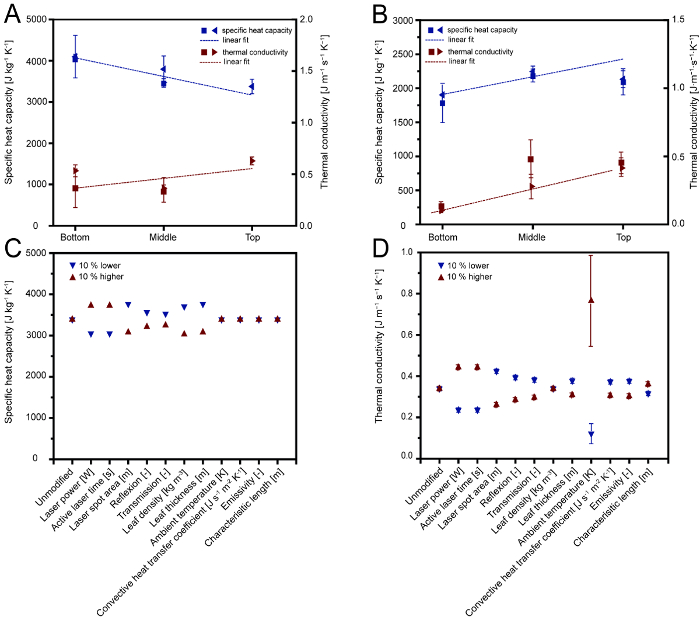
Figure 4: Specific heat capacity and thermal conductivity values determined for N. tabacum and N. benthamiana. A. Specific heat capacity and thermal conductivity of N. tabacum leaves according to the leaf position on the plant (bottom = old leaves; middle = mature leaves; top = young leaves). Stars and triangles indicate plants that were 49 and 56 days old, respectively. B. Specific heat capacity and thermal conductivity of N. benthamiana leaves according to the leaf position on the plant. Stars and triangles indicate plants that were cultivated in a phytotron or greenhouse, respectively. C. Sensitivity of specific heat capacity values to changes in the input parameters. Triangles show specific heat capacity values resulting from a 10% increase (red, upward) or decrease (blue, downward) in single model parameters. D. Sensitivity of thermal conductivity values to changes in the input parameters. Triangles mark shoe thermal conductivity values resulting from a 10% increase (red, upward) or decrease (blue, downward) in single model parameters. Error bars in A and B indicate the standard deviation (n≥3), while in C and D they represent the complete range of values obtained during 10% variation sensitivity analysis. Please click here to view a larger version of this figure.
Calculation of the Thermal Conductivity
The thermal conductivity (ʎ) was calculated from the temperature profiles by exponential fitting (Figure 3) combined with equations for conductive and convective heat transfer as well as thermal radiation. Equation 15 yielded average values of 0.49 ± 0.13 J m−1 s−1 K−1 (n = 19) for N. tabacum and 0.41 ± 0.20 J m−1 s−1 K−1 (n = 25) for N. benthamiana. There was no correlation between ʎ and plant age or cultivation setting, although a correlation between the leaf age and ʎ was observed for N. benthamiana (Figure 4B), agreeing with previously reported age-dependent differences in other plant species 14. As discussed above, the water content was an unlikely reason for this difference as it was found to be homogenous across leaves of varying maturity for N. benthamiana. Instead, we speculate that changes in the leaf tissue, e.g., the cell wall composition, were responsible for this observation by altering the heat transfer properties of the leaves and thus affecting the value of ʎ. The determination of ʎ was sensitive to changes in the ambient temperature. A sensitivity analysis revealed that fluctuations of ±2.3 K altered the value of ʎ by 64-125%. According to Equation 15, the ambient temperature has an effect by the power of four on the thermal radiation and thus directly affects the value of ʎ.
Evaluation of the Measurement Apparatus
It was possible to set up the measurement assembly within 3 h. Once this was complete, the start-up time of the system was approximately 15 min per measurement series. Single measurements took less than 3 min, including sample preparation and the entire measurement cycle. Analysis of the laser exposure time revealed that a heating time of 0.5 s resulted in a temperature increase of 19.9±4.3 °C (n=55) was the best compromise between the high ΔT (achieved by long laser pulses) required for a good signal-to-noise ratio (SNR) and the low ΔT (achieved by short laser pulses) required to avoid tissue damage. Pulse durations longer than 0.5 s resulted in the loss of mass from the sample, probably reflecting the evaporation of water and/or damage to the leaf tissue as the sample temperature reached up to 70 °C, whereas only 42.9±4.2 °C (n=55) were observed for 0.5 s laser pulses. For durations of less than 0.5 s, the temperature noise of ±0.31 K (standard deviation, n = 25) accounted for more than 5% of ΔT and was thus a significant part of ΔT. In contrast, at 0.5 s the noise accounted only for 2.5% of the signal and was thus regarded as insignificant. Additionally, the samples did not heat up to more than ~45 °C, which is a temperature that tobacco plants can also be exposed to in the natural tropic to sub-tropic habitat and which is only detrimental to plant species found in tundra habitats 15. The power density of the laser was 170 kW m-2, whereas natural solar radiation is typically in the range of 1.0-1.4 kW m-2 16,17. However, due to the very short time of the pulse, this higher energy dose did probably not damage the leaf tissue as indicated by a recently published microscopic analysis 11. The temperature data used to calculate ʎ were restricted to the initial 20 s after the laser pulse because only during this period did the noise (±0.31 K) account for less than 5% of the sample's temperature signal and was thus regarded as insignificant. When temperature data from beyond the 20 s time frame were used, the values calculated for ʎ declined (Figure 3F). A possible explanation was that some of the assumptions made for the calculation of ʎ did not apply for low values of ΔT. Especially, the term describing thermal radiation in Equation 15 might have been affected as it is affected by the forth power of temperature. Also, the leaf area surrounding the sample spot exposed to the laser might have heated up slightly and thus might not have been the ideal heat sink assumed in the model reducing the effective ΔTx and ultimately the calculated ʎ.
Discussion
The contact-free, non-destructive measurement method described above can be used to determine cp,s and ʎ in a simultaneous and reproducible manner. The calculation of ʎ in particular depends on several parameters that are sensitive to errors. Nevertheless, the impact of these errors was either linear or sub-proportional, and the coefficient of variation for all parameters was found to be less than 10%. Even though the method can thus be regarded as robust, some technical improvements can be made to reduce the remaining sources of error.
Mounting the sample into the assembly was technically challenging because a flat leaf surface is preferable for measurement but the sample naturally has an undulating surface. This problem could be overcome by designing a dedicated sample holder with geometries precisely adjusted to the leaf sample, e.g., leaf thickness and width, clamping the sample in the preferable orientation. This approach would make the measurements more reproducible, but would compromise the contact-free nature of the measurement because firm contact between the sample and holder would be required to pull the leaf surface flat. The benefits of using this kind of holder would therefore depend on the context of the measurement, i.e., whether the precision or contact-free nature of the measurement is most important. In contrast, such considerations may not be necessary at all for leaves with an inherently flat surface, e.g., rice and related species.
Convective heat transfer due to air movement in the environment of the sample should be kept to a minimum during measurements because this strongly affects the calculation of both cp,s and ʎ18. The apparatus should therefore be located away from air streams generated by air conditioning systems, radiators or other equipment, such as computer with integral cooling fans. This is also important because changes in the relative water content of the leaves 19 that might occur before or during the measurement due to evaporation, which can be increased by air movements 20, were not accounted for in the model. Thus, measurements, especially with detached leaves, should be carried out rapidly as described in the protocol section to avoid errors during data acquisition. In the future, the effects of evaporation on the measurement may be reduced or avoided if the measurement is conducted in an at least partially enclosed measurement chamber with an implemented humidity control.
The accuracy of cp,s and ʎ values can be increased by measuring the parameters used in the corresponding equations more precisely. In the case of cp,s these parameters are the laser power, maximum and ambient temperature and sample volume, i.e., the product of laser spot area and thickness, and sample density (Equation 8). The latter two parameters must be determined in experiments accompanying the actual measurement and their reliability can be improved if several representative biological replicates are tested. However, even when a simple dial-gauge measurement was used, the difference in leaf thickness compared to a microscopic analysis was only 11%, which affected the values calculated for cp,s and ʎ by the same degree. In contrast, temperatures and laser power can be monitored throughout the measurement. The accuracy of cp,s can be improved if these online data are used instead of fixed values for laser power and ambient temperature, and the data are collected using well-calibrated sensors. These considerations also apply to ʎ, but the ambient and sample temperatures are the most important parameters because both affect the calculated value by the power of four.
The current calculation of ʎ was based on several assumptions regarding convective heat transfer and thermal radiation. For example, the emissivity (ε) and convective heat transfer coefficient (h) were not measured or calculated explicitly in the method presented above, but were derived from previous publications 18,21. The accuracy of ʎ could therefore be improved by determining these two parameters under the actual measurement conditions. However, using the literature data for calculations nevertheless yielded ʎ values that were within the range experimentally determined for other plant species for which similar properties can be expected due to their phylogeny to Nicotiana species and their physiology, i.e., herbaceous plants 3. Even if the values for ε and h were varied over the entire range previously reported for these values in plants, e.g., 0.93-0.98 for ε 21, their effect on the final value of ʎ was <10% and thus within the natural variation observed here.
The method presented above was not only able to determine the thermal properties of intact unharmed leaves and detached leaves, but it also correctly identified different types of more severe damage introduced intentionally before measurement. Therefore, different types of leaf samples can be readily distinguished, providing a tool to remove, prior to analysis, any poor samples that would yield low-quality data. This feature could be used for quality control when monitoring biological materials, e.g., samples failing to meet specifications in terms of cp,s and ʎ could be excluded from further processing. This would be an asset in the context of a highly regulated processes such as molecular farming 4.
The advantages of this new method compared to others in the literature include the rapid sample handling, minimal preparation, contact-free and non-destructive simultaneous measurement of cp,s and ʎ, and the use of common equipment that can be found in many optical laboratories. This will facilitate broader applications of the method compared to those requiring specialized and expensive devices such as differential scanning calorimeters. Furthermore, calorimetry requires direct contact with the sample22 so there is a risk of damage, and the method is usually limited to the measurement of specific heat capacity 22. In contrast, whereas thermal imaging can detect necrosis or physical changes in leaves or entire plants in a contact-free manner 23, it also requires complex image analysis and dedicated specialized devices 24 which might be overcome in the future by cheaper and more powerful IR cameras and accompanying peripheral devices. Spectral analysis is another contact-free method for the analysis of water content and chlorophyll levels 25, but it has not yet been used to determine specific heat capacity and/or thermal conductivity.
The measurement approach reported herein is a robust method to determine the thermal properties of plant leaves with low investment costs and short measurement times. It was successfully used to determine cp,s and ʎ in N. tabacum and N. benthamiana, two species that are relevant in the area of molecular farming 4. The values calculated for both parameters based on leaf temperature profiles were in good agreement with those previously reported for other plant species 3. The method is non-destructive, contact-free, and does not require complex sample preparation, providing advantages over all current alternative methods for the analysis of thermal properties. The simple design may also facilitate the development of hand-held devices to increase flexibility.
Declarações
The authors have nothing to disclose.
Acknowledgements
The authors are grateful to Dr. Thomas Rademacher and Ibrahim Al Amedi for cultivating the plants used in this study. We would like to thank Dr. Richard M. Twyman for his assistance with editing the manuscript. This work was in part funded by the European Research Council Advanced Grant “Future-Pharma”, proposal number 269110, the Fraunhofer Zukunftsstiftung (Future Foundation), the Fraunhofer-Gesellschaft Internal Programs under Grant No. Attract 125-600164.
Materials
| 1" tube | Thorlabs | SM1L10E | Tube for fiber holder |
| Agarose | Sigma Aldrich | A0701 | Agarose |
| Bi-Convex lense f=25.4 | Thorlabs | LB1761 | Lense |
| Digital Handheld Optical Power and Energy Meter Console | Thorlabs | PM100D | Console for thermal surface absorber sensor |
| Digital Phosphor Oscilloscope | Tektronix | DPO7104 | Oscilloscope |
| DMR light microscope | Leica | n.a. | Light microscope |
| Falcon 50mL Conical Centrifuge Tubes | Fisher Scientific | 14-432-2 | Pycnometer |
| Ferty 2 Mega | Kammlott | 5.220072 | Fertilizer |
| Fiber holder | Thorlabs | Fiber holder | |
| Forma -86C ULT freezer | ThermoFisher | 88400 | Freezer |
| Greenhouse | n.a. | n.a. | For plant cultivation |
| Grodan Rockwool Cubes 10x10cm | Grodan | 102446 | Rockwool block |
| Infrared Detector Optris CT | Optris | OPTCTLT15 | Infrared detector |
| Infrared Detector Software Compact Connect | Optris | n.a. | Control software for infrared detector |
| Lambda 1050 UV/Vis spectrophotometer | PerkinElmer | L1050 | UV/VIS Spectrophotometer |
| Laser 400μm, 1550nm Conduction Cooled Single Bar Fiber Coupled Module | DILAS | M1F-SS2.1 | Laser |
| Laser cover | Amtron | LM200 | Laser Cover |
| Laser Driver | Amtron | CS 408 | Laser Driver |
| Osram cool white 36 W | Osram | 4930440 | Light source |
| Photodiode sensor | Thorlabs | PDA20H-EC | Power sensor for transmission measurements |
| Precision weight Ohaus Analytical Plus | Ohaus | 80251552 | Precision weight |
| Sample frame | Fraunhofer ILT | n.a. | Fixation of the leaf sample |
| Software Pyro Control | Amtron | n.a. | Laser Power Control Software |
| Stainless-steel-holder | n.a. | n.a. | Holder for measurement set-up |
| Teflon plates 2cm | Fraunhofer ILT | n.a. | Teflon attenuation |
| Thermal surface absorber Power sensor | Thorlabs | S314C | Sensor for laser power measurements |
| Vibratome | Leica | 1491200S001 | Vibratome |
| Zoc/Pro 6.51 | EmTec Innovative Software | n.a. | Laser Control Software |
Referências
- Wilhelm, E. . Heat Capacities: Liquids, Solutions and Vapours. , 516 (2010).
- Costa, J. M., Grant, O. M., Chaves, M. M. Thermography to explore plant-environment interactions. J. Exp. Bot. 64, 3937-3949 (2013).
- Jayalakshmy, M. S., Philip, J. Thermophysical Properties of Plant Leaves and Their Influence on the Environment Temperature. International Journal of Thermophysics. 31, 2295-2304 (2010).
- Buyel, J. F. Process development strategies in plant molecular farming. Curr. Pharm. Biotechnol. 16, 966-982 (2015).
- Schuster, A. C., et al. Effectiveness of cuticular transpiration barriers in a desert plant at controlling water loss at high temperatures. AoB PLANTS. 8, (2016).
- Parker, W. J., Jenkins, R. J., Abbott, G. L., Butler, C. P. Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity. J Appl Phys. 32, 1679-1684 (1961).
- Hays, R. L. The thermal conductivity of leaves. Planta. 125, 281-287 (1975).
- Menzel, S., et al. Optimized blanching reduces the host cell protein content and substantially enhances the recovery and stability of two plant derived malaria vaccine candidates. Front. Plant Sci. , (2015).
- Buyel, J. F., Hubbuch, J., Fischer, R. Blanching intact leaves or heat precipitation in an agitated vessel or heat exchanger removes host cell proteins from tobacco extracts. J. Vis. Exp. , (2015).
- Beiss, V., et al. Heat-precipitation allows the efficient purification of a functional plant-derived malaria transmission-blocking vaccine candidate fusion protein. Biotechnol. Bioeng. 112, 1297-1305 (2015).
- Buyel, J. F., Gruchow, H. M., Tödter, N., Wehner, M. Determination of the thermal properties of leaves by non-invasive contact free laser probing. J. Biotechnol. 217, 100-108 (2016).
- Buyel, J. F. Numeric simulation can be used to predict heat transfer during the blanching of leaves and intact. Biochem. Eng. J. , (2015).
- Hedlund, H., Johansson, P. Heat capacity of birch determined by calorimetry: implications for the state of water in plants. Thermochim Acta. 349, 79-88 (2000).
- Chandrakanthi, M., Mehrotra, A. K., Hettiaratchi, J. P. A. Thermal conductivity of leaf compost used in biofilters: An experimental and theoretical investigation. Environ. Pollut. 136, 167-174 (2005).
- Larcher, W. . Physiological Plant Ecology: Ecophysiology and Stress Physiology of Functional Groups. , (2003).
- Cowen, R. A gamma-ray burst’s enduring fireball. Science News. 152, 197 (1997).
- Jones, H. G., et al. Thermal infrared imaging of crop canopies for the remote diagnosis and quantification of plant responses to water stress in the field. Funct. Plant Biol. 36, 978-989 (2009).
- Defraeye, T., Verboven, P., Ho, Q. T., Nicolai, B. Convective heat and mass exchange predictions at leaf surfaces: Applications, methods and perspectives. Comput. Electron. Agric. 96, 180-201 (2013).
- Arndt, S. K., Irawan, A., Sanders, G. J. Apoplastic water fraction and rehydration techniques introduce significant errors in measurements of relative water content and osmotic potential in plant leaves. Physiol. Plant. 155, 355-368 (2015).
- Jones, H. G., Schofield, P. Thermal and other remote sensing of plant stress. General and Applied Plant Physiology. 34, 19-32 (2008).
- Jones, H. G., Archer, N., Rotenberg, E., Casa, R. Radiation measurement for plant ecophysiology. J. Exp. Bot. 54, 879-889 (2003).
- Dupont, C., Chiriac, R., Gauthier, G., Toche, F. Heat capacity measurements of various biomass types and pyrolysis residues. Fuel. 115, 644-651 (2014).
- Chaerle, L., et al. Multi-sensor plant imaging: Towards the development of a stress-catalogue. Biotechnol. J. 4, 1152-1167 (2009).
- Hackl, H., Baresel, J. P., Mistele, B., Hu, Y., Schmidhalter, U. A Comparison of Plant Temperatures as Measured by Thermal Imaging and Infrared Thermometry. J. Agron. Crop. Sci. , 415-429 (2012).
- Yuan, L., et al. Spectral analysis of winter wheat leaves for detection and differentiation of diseases and insects. Field Crops Res. 156, 199-207 (2014).

