Energy Stored In A Coaxial Cable

A coaxial cable consists of a central copper conductor used for transmitting signals, followed by an insulator shield, a metallic braided mesh that prevents signal interference, and a plastic layer that encases the entire assembly.

In the simplest form, a coaxial cable can be represented by two long hollow concentric cylinders in which the current flows in opposite directions. The magnetic field inside and outside the coaxial cable is determined by using Ampère's law. The magnetic field inside the inner conductor is zero, as no current is enclosed in that region. The magnetic field outside the cable is also zero because the oppositely flowing currents in the two concentric cylinders cancel each other, giving zero net currents. The magnetic field exists only in the shell region between the two conductors and is used to obtain the expression for the energy density of the magnetic field.

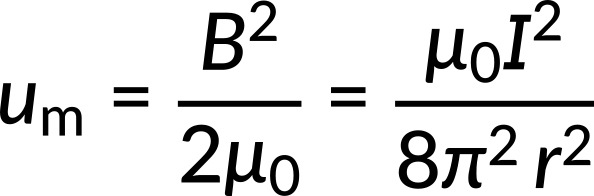
All of the cable's magnetic energy is stored between the two conductors. The magnetic energy is calculated by an integral of the magnetic energy density times the differential volume over the cylindrical shell.

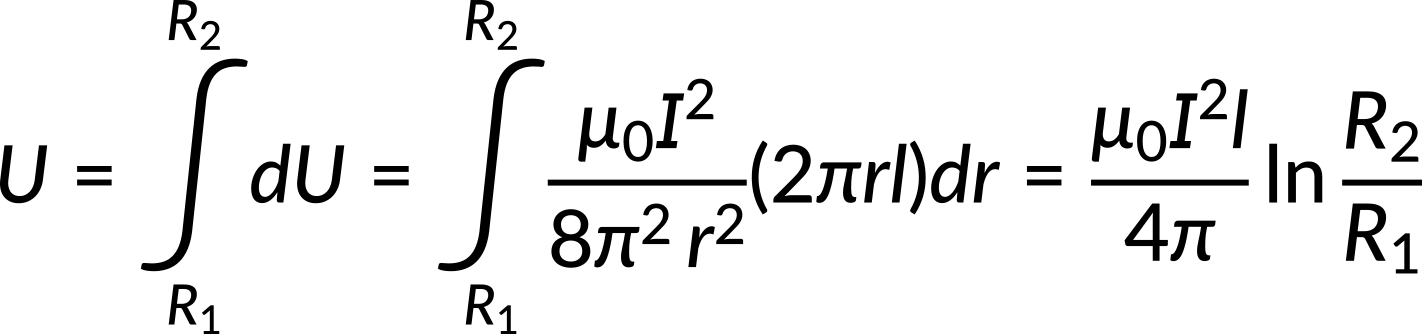
The magnetic energy per unit length is directly proportional to the square of the current. The total energy can also be expressed in terms of the self-inductance of the coaxial cable.

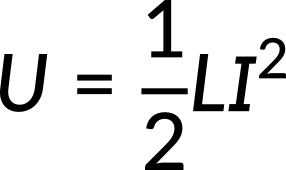
Equating these two expressions results in an expression for the self-inductance per unit length for a coaxial cable, which depends only on the inner and outer radii of the cable.

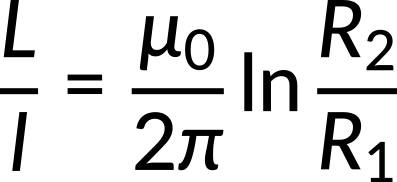
Inductance can be increased by increasing the outer radius or by decreasing the inner radius.

In the limit, when the inner radius reaches the outer radius, the inductance becomes zero, and the cable is no longer coaxial.