Path Between Thermodynamics States

Consider the two thermodynamic processes involving an ideal gas that are represented by paths AC and ABC in Figure 1:

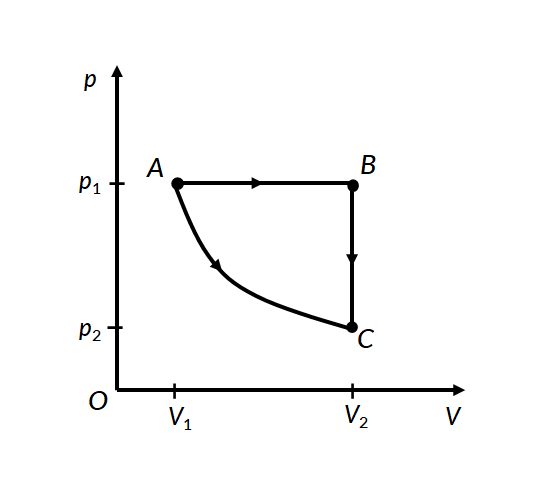
In the first process for path A に C, the gas is kept at constant temperature T. It undergoes an expansion from volume V₁ に V₂.

The work done by an ideal gas is expressed as

Substituting for pressure as nRT/V from the ideal gas equation and integrating the terms, the work done by an ideal gas at constant temperature is obtained as

In the second process, for path A に B, the ideal gas is first expanded from volume V₁ に V₂ at constant pressure p₁ by applying heat. The gas is then cooled at constant volume V₂ along path B に C, such that its pressure drops to p₂.

For path A に B, work is done under constant pressure, therefore

For path B に C, since the volume remains constant, no work is done by the gas or on the gas by the surroundings. Therefore the total work done by the gas in this process is the same as the work done for path A に B.

In both processes, the gas expands from volume V₁ to volume V₂, such that its pressure changes from p₁ に p₂. However, the work done in both processes is different. This proves that work done by a system is path-dependent.