10.8:
Crystal Field Theory – Octahedral Complexes
23,033 Views
•
•
Crystal Field Theory
To explain the observed behavior of transition metal complexes (such as colors), a model involving electrostatic interactions between the electrons from the ligands and the electrons in the unhybridized d orbitals of the central metal atom has been developed. This electrostatic model is crystal field theory (CFT). It helps to understand, interpret, and predict the colors, magnetic behavior, and some structures of coordination compounds of transition metals.
CFT focuses on the nonbonding electrons on the central metal ion in coordination complexes not on the metal-ligand bonds. Like valence bond theory, CFT tells only part of the story of the behavior of complexes. In its pure form, CFT ignores any covalent bonding between ligands and metal ions. Both the ligand and the metal are treated as infinitesimally small point charges.
All electrons are negative, so the electrons donated from the ligands will repel the electrons of the central metal. Consider the behavior of the electrons in the unhybridized d orbitals in an octahedral complex. The five d orbitals consist of lobe-shaped regions and are arranged in space, as shown in Figure 1. In an octahedral complex, the six ligands coordinate along the axes.
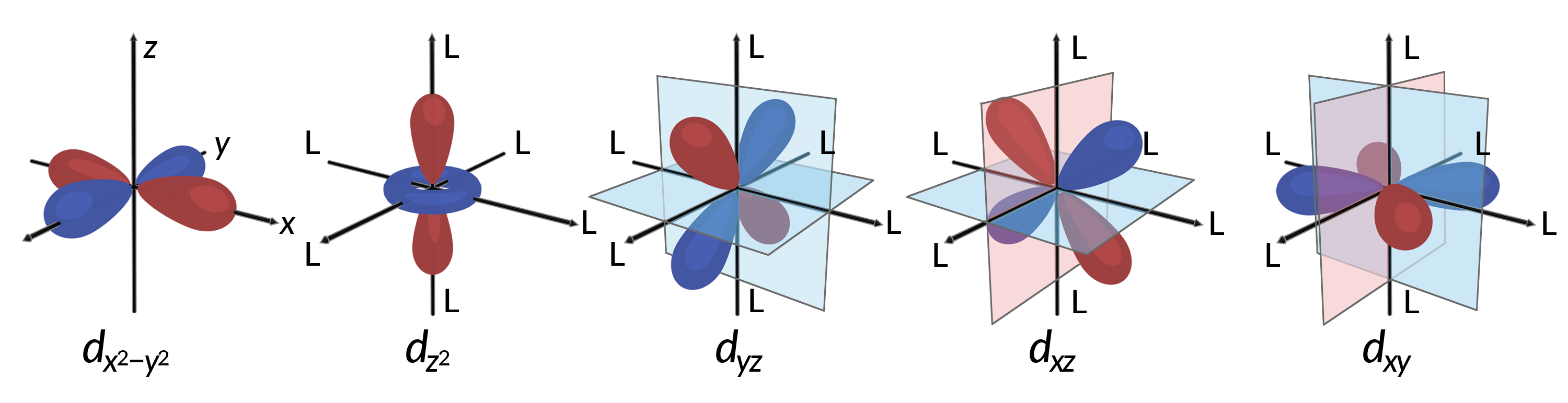
Figure 1. The directional characteristics of the five d orbitals are shown here. The shaded portions indicate the phase of the orbitals. The ligands (L) coordinate along the axes in octahedral complexes. For clarity, the ligands have been omitted from the dx2−y2 orbital so that the axis labels could be shown.
In an uncomplexed metal ion in the gas phase, the electrons are distributed among the five d orbitals in accord with Hund's rule because the orbitals all have the same energy. In transition metal complexes, the energies of the d orbitals of transition metal atoms are affected by the type of ligands and the molecular geometry. If the ligand molecules are uniformly arranged around the metal ion, a spherical crystal field is created. This spherical crystal field raises the energies of the d orbitals of the metal ion by an equal amount (Figure 2). When the ligands coordinate to a metal ion in an octahedral geometry, the energies of the d orbitals are no longer the same.
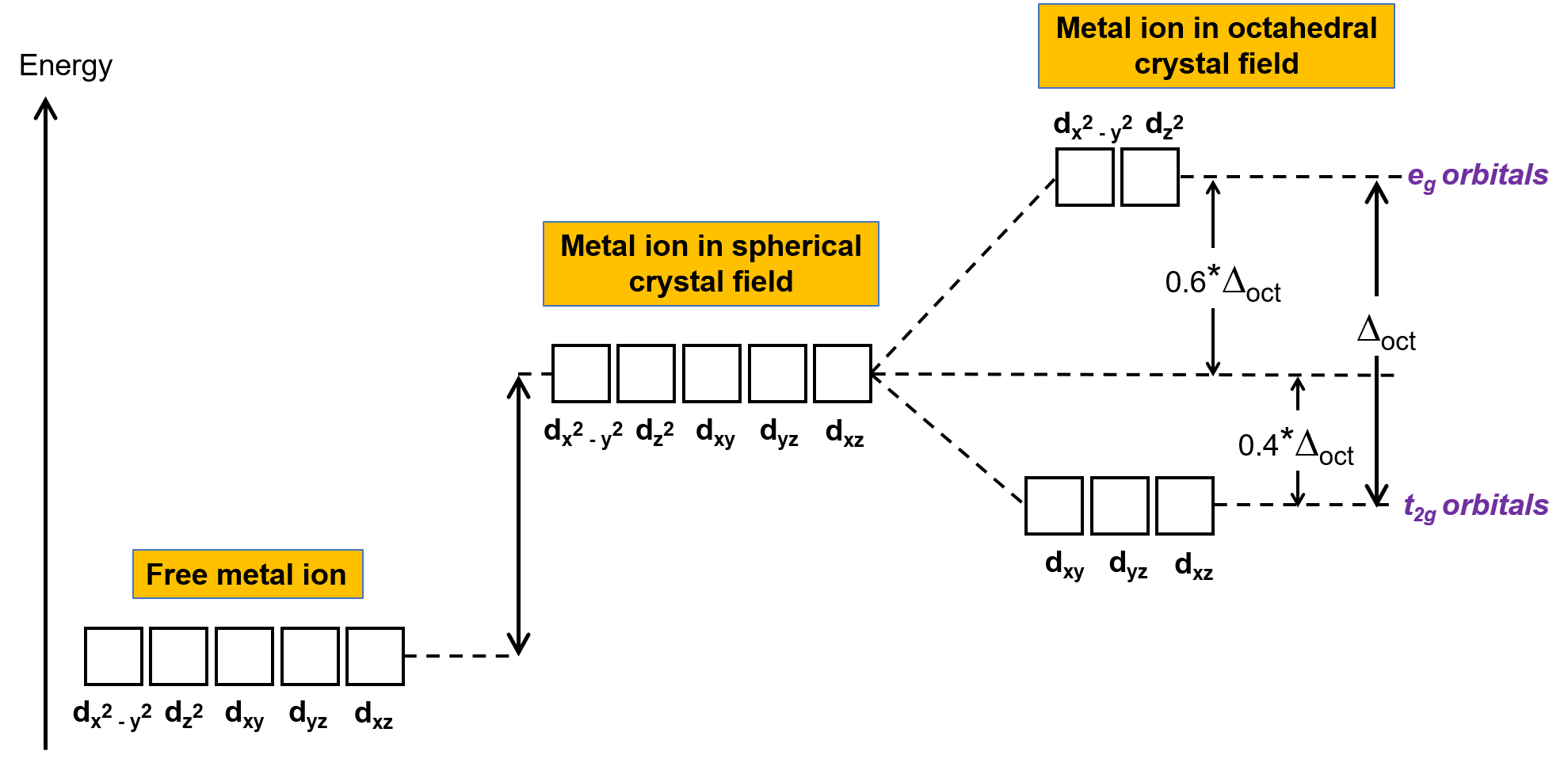
Figure 2. The d orbitals of the metal ion in a spherical crystal field are destabilized (higher in energy) in comparison to the d orbitals of the uncomplexed free metal ion. In octahedral complexes, the eg orbitals are further destabilized (higher in energy) compared to the t2g orbitals because the ligands interact more strongly with the d orbitals at which they are pointed directly.
In octahedral complexes, the lobes in two of the five d orbitals, the dx2−y2 and dz2 orbitals, point toward the ligands (Figure 1). These two orbitals are called the eg orbitals (the symbol refers to the symmetry of the orbitals). The other three orbitals, the dxy, dxz, and dyz orbitals, have lobes that point between the ligands and are called the t2g orbitals (again, the symbol refers to the symmetry of the orbitals). As six ligands approach the metal ion along the axes of the octahedron, their point charges repel the electrons in the d orbitals of the metal ion. However, the repulsions between the electrons in the eg orbitals (the dx2–y2 orbitals) and the ligands are greater than the repulsions between the electrons in the t2g orbitals (the dxy, dxz, and dyz orbitals) and the ligands. This is because the lobes of the eg orbitals point directly at the ligands, whereas the lobes of the t2g orbitals point between them. Thus, electrons in the eg orbitals of the metal ion in an octahedral complex have higher potential energies than those of electrons in the t2g orbitals. The difference in energy may be represented as shown in Figure 2.
The difference in energy between the eg and the t2g orbitals is called the crystal field splitting and is symbolized by Δoct, where oct stands for octahedral. The magnitude of Δoct depends on many factors, including the nature of the six ligands located around the central metal ion, the charge on the metal, and whether the metal is using 3d, 4d, or 5d orbitals. Different ligands produce different crystal field splittings. The increasing crystal field splitting produced by ligands is expressed in the spectrochemical series, a short version of which is given here:

This text is adapted from Openstax, Chemistry 2e, Section:19.3: Spectroscopic and Magnetic Properties of Coordination Compounds.
