Demi-vie d'une réaction

Le temps de demi-réaction (t_1/2) est le temps nécessaire à la consommation de la moitié d’une quantité donnée de réactif. À chaque temps de demi-réaction successif, la moitié de la concentration restante du réactif est consommée. Par exemple, pendant la décomposition du peroxyde d’hydrogène, pendant le premier temps de demi-réaction (de 0,00 heure à 6,00 heures), la concentration de H₂O₂ diminue de 1,000 M à 0,500 M. Pendant le deuxième temps de demi-réaction (de 6,00 heures à 12,00 heures), la concentration diminue de 0,500 M à 0,250 M. Pendant le troisième temps de demi-réaction, elle chute de 0,250 M à 0,125 M. Par conséquent, pendant chaque période successive de 6,00 heures, la concentration d’H₂O₂ diminue de moitié.

Le temps de demi-réaction d’une réaction de premier ordre est indépendante de la concentration du réactif. Cependant, le temps de demi-réaction des réactions ayant d’autres ordres dépend des concentrations des réactifs.

Temps de demi-réaction pour les réactions du premier ordre

Une équation reliant le temps de demi-réaction d’une réaction de premier ordre à sa constante de vitesse peut être déduite de sa loi de vitesse intégrée :

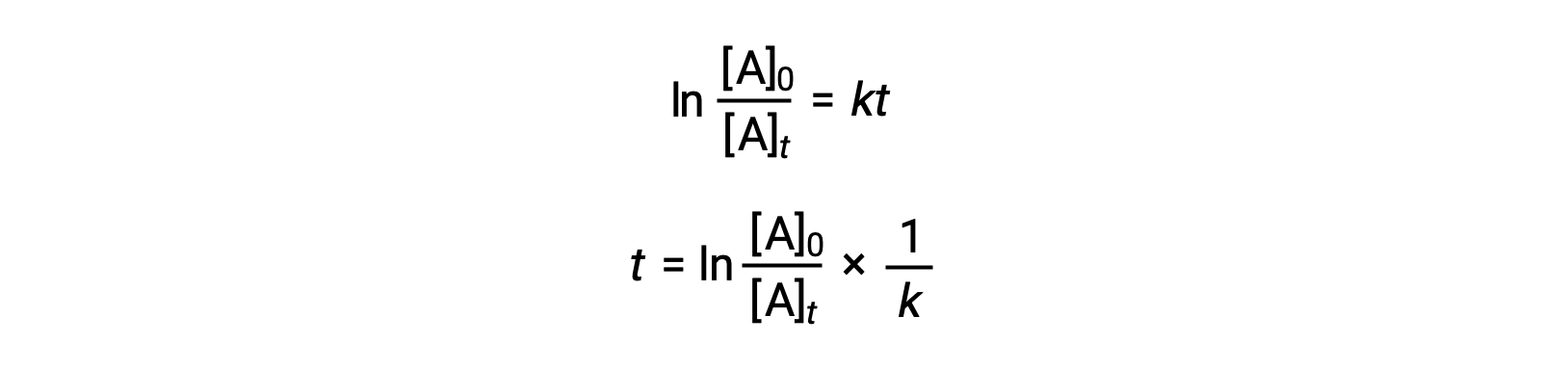
D’après la définition du temps de demi-réaction, au moment t_1/2, la concentration du réactif A est égale à la moitié de sa concentration initiale. Par conséquent, t = t_1/2  et [A]_t = ½ [A]₀.

En substituant ces termes dans la loi de vitesse intégrée réorganisée et en simplifiant, cela donne l’équation du temps de demi-réaction :

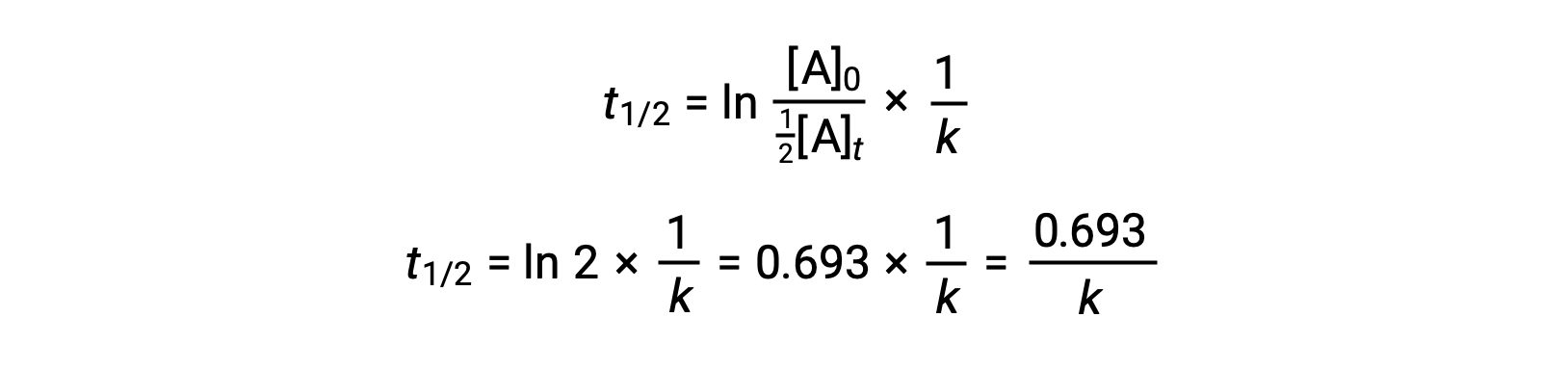
Cette équation du temps de demi-réaction décrit une relation inverse à laquelle on s’attend entre le temps de demi-réaction d’une réaction et sa constante de vitesse, k. Les réactions plus rapides présentent des constantes de vitesse plus grandes et des temps de demi-réaction plus courts, tandis que les réactions plus lentes présentent des constantes de vitesse plus petites et des temps de demi-réaction plus longs.

Temps de demi-réaction pour les réactions du deuxième ordre

Suivant la même approche que pour les réactions du premier ordre, une équation reliant le temps de demi-réaction d’une réaction du deuxième ordre à sa constante de vitesse et à sa concentration initiale peut être déduite de sa loi de vitesse intégrée :  

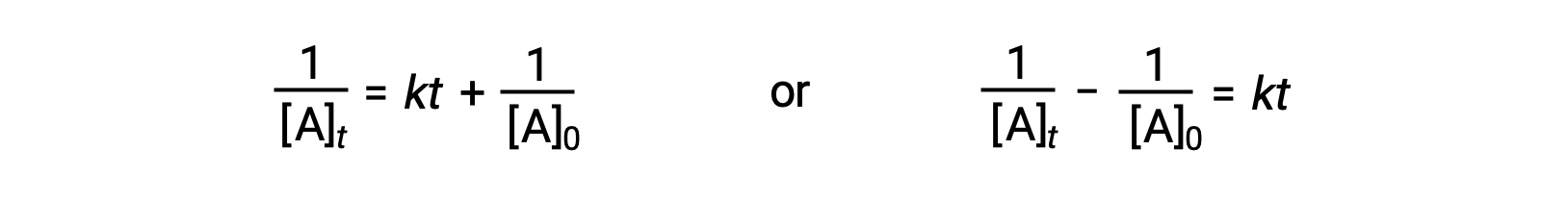
En remplaçant t = t_1/2  et [A]_t = ½[A]₀, la loi de vitesse intégrée est simplifiée :

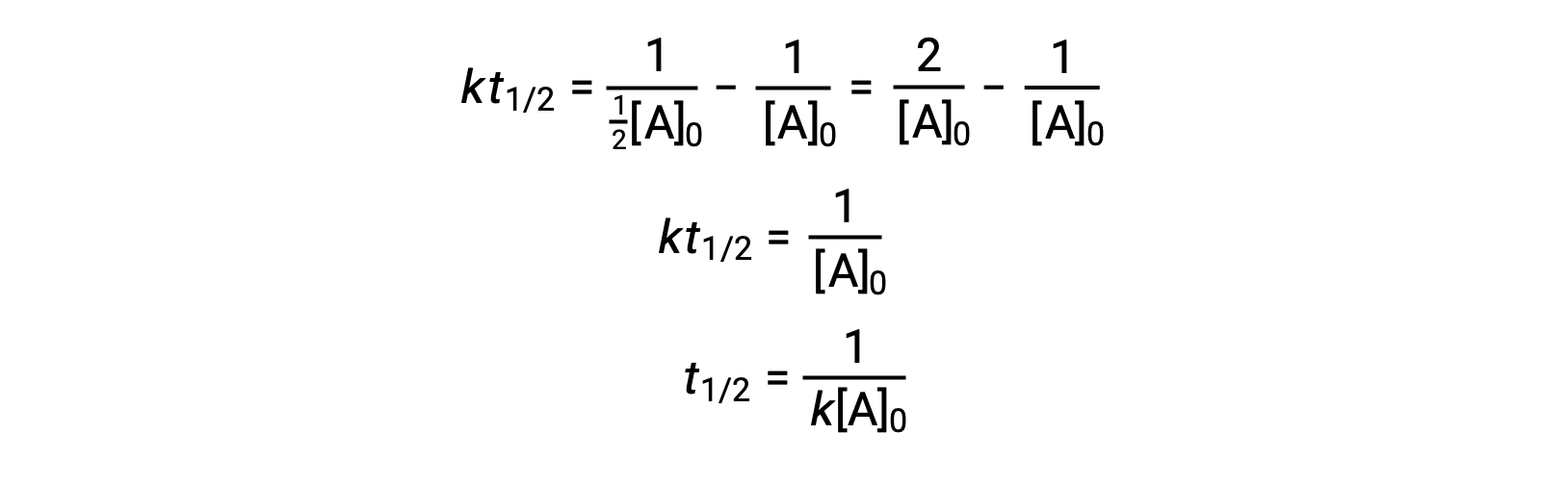
Pour une réaction du deuxième ordre, t_1/2 est inversement proportionnel à la concentration du réactif, et le temps de demi-réaction augmente au fur et à mesure que la réaction se poursuit, car la concentration du réactif diminue. Contrairement aux réactions du premier ordre, la constante de vitesse d’une réaction du deuxième ordre ne peut pas être calculée directement à partir du temps de demi-réaction à moins que la concentration initiale ne soit connue.

Temps de demi-réaction pour les réactions d’ordre zéro

Une équation du temps de demi-réaction d’ordre zéro peut également être déduite de sa loi de vitesse intégrée :   

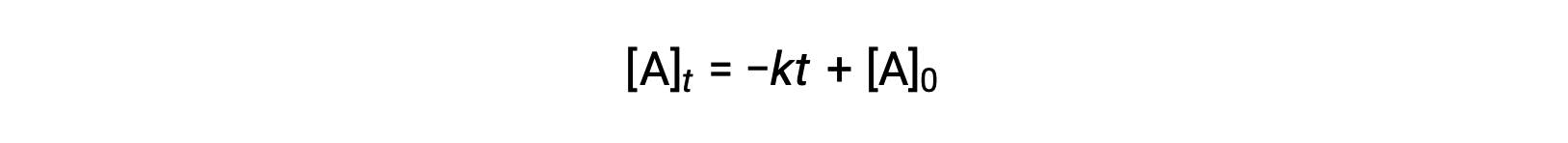
La substitution de t = t_1/2  et  [A]_t = ½ [A]₀, dans la loi de vitesse intégrée d’ordre zéro donne :

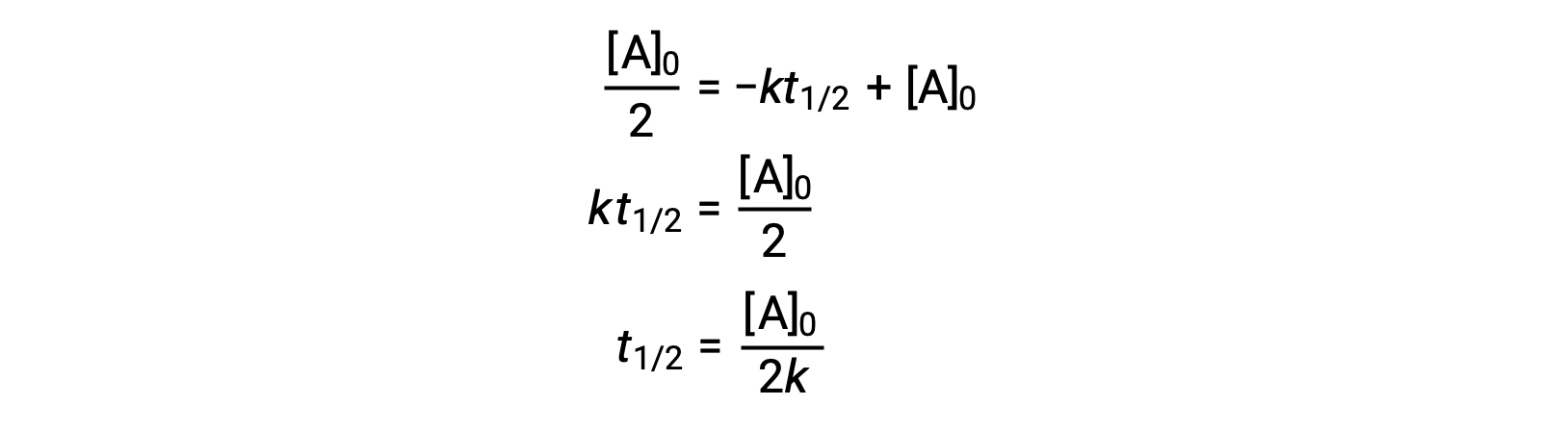
Le temps de demi-réaction d’une réaction d’ordre zéro est inversement proportionnelle à sa constante de vitesse. Cependant, le temps de demi-réaction d’une réaction d’ordre zéro augmente à mesure que la concentration initiale augmente.

Ce texte est adapté de Openstax, Chimie 2e, Section 12.4 : Lois de vitesse intégrées