Optimizing Magnetic Force Microscopy Resolution and Sensitivity to Visualize Nanoscale Magnetic Domains

Audrey C. Parker; Olivia O. Maryon; Mojtaba T. Kaffash; M. Benjamin Jungfleisch; Paul  H. Davis

doi:10.3791/64180

JoVE Journal > Engineering

Ingénierie

Optimizing Magnetic Force Microscopy Resolution and Sensitivity to Visualize Nanoscale Magnetic Domains

Published: July 20, 2022

doi:

10.3791/64180

Audrey C. Parker*¹, Olivia O. Maryon*¹, Mojtaba T. Kaffash², M. Benjamin Jungfleisch², Paul H. Davis^1,3

¹Micron School of Materials Science & Engineering,Boise State University, ²Department of Physics and Astronomy,University of Delaware, ³Center for Advanced Energy Studies

Summary

Magnetic force microscopy (MFM) employs a vertically magnetized atomic force microscopy probe to measure sample topography and local magnetic field strength with nanoscale resolution. Optimizing MFM spatial resolution and sensitivity requires balancing decreasing lift height against increasing drive (oscillation) amplitude, and benefits from operating in an inert atmosphere glovebox.

Abstract

Magnetic force microscopy (MFM) enables mapping local magnetic fields across a sample surface with nanoscale resolution. To perform MFM, an atomic force microscopy (AFM) probe whose tip has been magnetized vertically (i.e., perpendicular to the probe cantilever) is oscillated at a fixed height above the sample surface. The resultant shifts in the oscillation phase or frequency, which are proportional to the magnitude and sign of the vertical magnetic force gradient at each pixel location, are then tracked and mapped. Although the spatial resolution and sensitivity of the technique increases with decreasing lift height above the surface, this seemingly straightforward path to improved MFM images is complicated by considerations such as minimizing topographical artifacts due to shorter range van der Waals forces, increasing the oscillation amplitude to further improve sensitivity, and the presence of surface contaminants (in particular water due to humidity under ambient conditions). In addition, due to the orientation of the probe’s magnetic dipole moment, MFM is intrinsically more sensitive to samples with an out-of-plane magnetization vector. Here, high-resolution topographical and magnetic phase images of single and bicomponent nanomagnet artificial spin-ice (ASI) arrays obtained in an inert (argon) atmosphere glovebox with <0.1 ppm O₂ and H₂O are reported. Optimization of lift height and drive amplitude for high resolution and sensitivity while simultaneously avoiding the introduction of topographical artifacts is discussed, and detection of the stray magnetic fields emanating from either end of the nanoscale bar magnets (~250 nm long and <100 nm wide) aligned in the plane of the ASI sample surface is shown. Likewise, using the example of a Ni-Mn-Ga magnetic shape memory alloy (MSMA), MFM is demonstrated in an inert atmosphere with magnetic phase sensitivity capable of resolving a series of adjacent magnetic domains each ~200 nm wide.

Introduction

Magnetic force microscopy (MFM), a scanning probe microscopy (SPM) derivative of atomic force microscopy (AFM), enables imaging of the relatively weak but long-range magnetic forces experienced by a magnetized probe tip as it travels above a sample surface¹^,²^,³^,⁴^,⁵. AFM is a non-destructive characterization technique that employs a nanometer-scale tip at the end of a pliable cantilever to map surface topography⁶ as well as measure material (e.g., mechanical, electrical, and magnetic) properties⁷^,⁸^,⁹ with nanoscale resolution. Deflection of the cantilever due to tip-sample interactions of interest is measured via reflection of a laser off the back of the cantilever and into a position-sensitive photodiode¹⁰. High-resolution imaging of a material's local magnetic properties via MFM provides the unique opportunity to characterize the magnetic field strength and orientation in novel materials, structures, and devices at the nanoscale⁴^,⁵^,¹¹^,¹²^,¹³^,¹⁴^,¹⁵^,¹⁶^,¹⁷. To perform MFM, an AFM probe whose tip has been magnetized vertically (i.e., perpendicular to the probe cantilever and sample surface) is mechanically oscillated at its natural resonance frequency at a fixed height above the sample surface. Resultant changes in oscillation amplitude (less sensitive, and hence less common), frequency, or phase (described here) are then monitored to measure magnetic field strength qualitatively. More specifically, frequency modulation MFM produces a map of shifts in the oscillation frequency or phase, proportional to the magnitude and sign of the magnetic force gradient experienced by the probe. In order to maintain a constant height above the sample during MFM measurements, a dual-pass mode of operation is typically employed. The sample topography is first mapped via standard AFM techniques, followed by interleaved MFM imaging of each sequential scan line at a user-determined lift height (tens to hundreds of nm) off the sample surface. Employing such an interleaved dual-pass acquisition mode enables separation of the short-range tip-sample van der Waals interactions used to map the topography from the relatively longer-range magnetic forces experienced during the interleaved lift mode pass. However, MFM spatial resolution increases with decreasing lift height¹⁸, so there is an inherent tension between increasing MFM resolution and avoiding topographical artifacts due to van der Waals forces. Likewise, MFM sensitivity is proportional to the oscillation amplitude during the lift mode pass, but the maximum allowable oscillation amplitude is limited by the lift height and rapid changes in sample topography (i.e., high aspect ratio features).

Recent studies have highlighted the wealth of opportunities associated with the application of nanomagnetism and nanomagnonics, developed via artificial spin-ice (ASI) structures and magnonic crystals, as functioning devices for logic, computation, encryption, and data storage¹⁹^,²⁰^,²¹^,²². Composed of nanomagnets arranged in distinct extended lattice formations, artificial spin ices exhibit emergent magnetic dipoles or monopoles that can be controlled via an external stimulus¹⁹^,²⁰^,²³^,²⁴^,²⁵. In general, ASIs favor a moment configuration that minimizes the energy (e.g., in a two-dimensional (2D) square ASI, two moments point in and two point out of every vertex), with the low energy microstates following rules analogous to crystalline spin-ice materials²¹^,²⁶^,²⁷^,²⁸. Similarly, a recent MFM-enabled study demonstrated a three-dimensional (3D) ASI lattice system constructed from rare-earth spins situated on corner-sharing tetrahedra, where two spins point toward the center of the tetrahedra and two spins point out, resulting in two equal and opposite magnetic dipoles and hence a net zero magnetic charge at the tetrahedra centers²³. Depending upon the alignment of an applied magnetic field relative to the sample surface, significant differences in the magnetic ordering and correlation length were observed. The alignment and control of ASI dipoles thus warrant further investigation. Methods for measuring ASI magnetic field distributions have included using a magneto-optical noise spectrometer²⁹ or X-ray magnetic circular dichroism photoemission electron microscopy (XMCD-PEEM)²⁵; however to achieve spatial resolutions equal to or greater than that of MFM with XMCD-PEEM, extremely short wavelengths (i.e., high energy X-rays) are required. MFM offers a much simpler characterization technique that does not require exposure of samples to potentially damaging high energy X-rays. Additionally, MFM has been used to not only characterize ASI microstates²¹^,²³^,²⁷, but also for topological defect driven magnetic writing using high magnetic moment tips³⁰. Accordingly, MFM can play a vital role in furthering ASI research and development, specifically through its ability to correlate sample topography with magnetic field strength and orientation, thereby revealing the magnetic dipoles associated with specific topographic features (i.e., ASI lattice elements).

High-resolution MFM likewise provides significant insight into the relationship between the structure of ferromagnetic shape memory alloys and their nanoscale magnetomechanical properties¹⁴^,¹⁷^,³¹^,³²^,³³. Ferromagnetic shape memory alloys, commonly referred to as magnetic shape memory alloys (MSMAs), exhibit large (up to 12%) magnetic field induced strains, carried through twin boundary motion²⁹^,³³^,³⁴^,³⁵. MFM techniques have been used to investigate the complex relationships between twinning during deformation and martensitic transformation, indentation, micro-pillar deformation, and nanoscale magnetic responses of MSMAs¹⁵^,¹⁶^,¹⁷^,³⁶. Of particular note, MFM has been combined with nanoindentation to create and read a four-state nanoscale magnetomechanical memory¹⁷. Similarly, next-generation magnetic recording technologies are being pursued via heat-assisted magnetic recording (HAMR), achieving linear densities of 1975 kBPI and track densities of 510 kTPI³⁷. The increased areal density required to enable greater, more compact data storage has resulted in a significant reduction in the defined track pitch of HAMR technologies, accentuating the need for high-resolution MFM imaging.

In addition to ASIs and MSMAs, MFM has been successfully used to characterize various magnetic nanoparticles, nanoarrays, and other types of magnetic samples³^,³⁸^,³⁹. However, ultimate MFM resolution and sensitivity are limited both by things beyond the user's control (e.g., AFM detection electronics, MFM probe technology, underlying physics, etc.) and by choice of imaging parameters and environment. Meanwhile, feature sizes in magnetic devices continue to decrease⁴⁰^,⁴¹, creating smaller magnetic domains, thus making MFM imaging increasingly more challenging. Additionally, the magnetic dipoles of interest are not always oriented out-of-plane, parallel to the magnetization vector of the probe. High-resolution imaging of the stray fields emanating from the ends of in-plane or nearly in-plane oriented dipoles, as is the case in the ASI structures shown here, requires greater sensitivity. Achieving high-resolution MFM images, especially of such in-plane magnetized samples composed of nanoscale magnetic domains, thus depends on appropriate choice of MFM probe (e.g., thickness, coercivity, and moment of the magnetic coating, which can at times be at odds with improving sensitivity or lateral resolution¹⁸ or preservation of the sample's magnetic alignment³⁰), imaging parameters (e.g., lift height and oscillation amplitude, as mentioned above, as well as minimizing tip coating wear during topography line imaging), and sample quality (e.g., surface roughness and contamination, including polishing debris or surface water due to ambient humidity). In particular, the presence of water adsorbed on the sample surface due to ambient humidity can introduce strong tip-sample van der Waals forces that can significantly interfere with measuring magnetic forces and limit the minimum achievable lift height for MFM measurements. MFM operation within an inert atmosphere glovebox eliminates nearly all surface contaminants, allowing for lower lift heights and higher resolution coupled with greater sensitivity. Accordingly, in the sample examples shown here, an AFM system housed in a custom inert atmosphere glovebox filled with argon (Ar) containing <0.1 ppm oxygen (O₂) and water (H₂O) has been employed to enable extremely low lift heights (down to 10 nm). This subsequently enables exquisitely high-resolution MFM imaging capable of resolving alternating magnetic domains <200 nm wide within a larger crystallographic twin and magnetic dipoles (nanoscale bar magnets) <100 nm wide and ~250 nm long.

This article explains how to acquire high-resolution, high-sensitivity MFM images by combining the use of an inert atmosphere glovebox with careful sample preparation and optimal choice of imaging parameters. The described methods are especially valuable for imaging in-plane oriented dipoles, which are traditionally difficult to observe, and therefore exemplary high-resolution MFM images are presented of both Ni-Mn-Ga MSMA crystals exhibiting distinct nanoscale magnetic domains within crystallographic twins and across twin boundaries, as well as nanomagnetic ASI arrays fabricated with an in-plane magnetic dipole orientation. Researchers in a wide variety of fields desiring high-resolution MFM imaging can significantly benefit from employing the protocol outlined here, as well as the discussion of potential challenges such as topographical artifacts.

Protocol

NOTE: In addition to the protocol below, a detailed step-by-step MFM standard operating procedure (SOP) specific to the instrument used here and geared towards general MFM imaging is included as Supplementary File 1. To supplement the video portion of this manuscript, the SOP includes images of the probe holder, tip magnetizer and magnetization procedure, software settings, etc.

1. MFM probe preparation and installation

Open the AFM control software and select the MFM workspace (see Table of Materials).
Mount an AFM probe with a magnetic coating (e.g., Co-Cr, see Table of Materials) on an appropriate probe holder (see Table of Materials), magnetize the probe, and install the probe holder on the AFM head.
NOTE: MFM probes require a magnetic coating; the probes used in this study utilized a cobalt-chromium (Co-Cr) alloy coating with a nominal coercivity of 400 Oe and a magnetic moment of 1 x 10^-13 EMU, resulting in an ~35 nm radius of curvature for the coated n-doped silicon probe. Probes with a smaller radius of curvature or lower or higher magnetic moment or coercivity are available, depending upon sample and imaging needs (e.g., a low moment probe may be needed when imaging a low coercivity sample to avoid inadvertently flipping the magnetization direction of the sample with the probe, or conversely a high moment probe may be used to write a magnetic pattern¹⁸). See the Table of Materials for an extensive, but non-exhaustive, list of MFM probe options, keeping in mind that a thinner magnetic coating will yield a sharper MFM tip (and hence potentially improved spatial resolution) but at the likely cost of decreased sensitivity due to a lower magnetic moment.
1. Carefully place the probe holder on a mounting block (see Supplementary Figure S1), then load the probe onto the probe holder, align, and secure in place with a spring-loaded clip (see Supplementary Figure S2). Ensure the probe is parallel to all edges and not touching the back of the holder's channel by inspecting it under an optical microscope. Gently manipulate the probe as necessary with a pair of tweezers.
  NOTE: Electrostatic discharge (ESD) can damage the metallic coating on the MFM probe and/or sensitive AFM electronics, so be careful to discharge any static buildup prior to handling and consider wearing anti-ESD gloves and/or using a grounding wrist strap or mat depending on the environmental conditions (e.g., relative humidity).
2. Magnetize the probe vertically (i.e., perpendicular to the probe cantilever) using a strong permanent magnet (see Table of Materials) for a few (~2-5) seconds so that the magnetic dipole orientation of the probe tip will be perpendicular to the sample.
  NOTE: For reference, the probe magnetizer used here (see Table of Materials and Supplementary Figure S3) has a coercivity of ~2000 Oe and is designed so that the case fits over the probe holder, with the magnet oriented such that its magnetic moment is aligned parallel to the probe tip and perpendicular to the cantilever.
3. Carefully remove the AFM head. Install the probe and probe holder by aligning the holes on the probe holder with the contact pins on the head. Reinstall the head on the AFM and secure in place. Again, be careful as ESD can damage the probe or sensitive AFM electronics.
Align the laser onto the center of the MFM probe cantilever and into the position-sensitive detector (PSD).
1. For optimal sensitivity, align the laser on the back of the cantilever to the location corresponding to the tip setback from the distal end of the cantilever.
2. Maximize the sum signal on the PSD while minimizing the left/right and up/down deflections to center the reflected laser beam on the detector. Set the laser X and Y deflection signals as close to zero as possible to obtain maximum detectable deflection range for producing an output voltage proportional to the cantilever deflection.

2. Sample preparation and installation

Place the sample over the AFM chuck vacuum port. Avoid using a magnetic sample holder, as this could affect the sample and/or interfere with the MFM measurement. Turn on the chuck vacuum to secure the sample to the AFM stage.
1. Secure the sample well for imaging to avoid introduction of noise due to nanoscale sample vibrations. If an airtight seal cannot be formed between the base of the sample and the AFM stage vacuum port, affix the sample to a metal puck (see Table of Materials) or glass microscope slide using an appropriate bonding adhesive.
2. Ensure that the sample is as smooth as possible, ideally with nanometer scale surface roughness and free of debris (e.g., residual polishing compound in the case of a metal alloy sample such as single crystal Ni-Mn-Ga), to enable low lift heights leading to high resolution and sensitivity of MFM imaging (see Discussion).

3. Initial setup and sample approach

Returning to the AFM control software (MFM workspace), align the crosshairs within the optical microscope view to be positioned over the back of the MFM probe cantilever where the tip is located, using the known tip setback based on the selected probe.
Position the AFM stage and sample so that the region of interest (ROI) is directly beneath the AFM tip. Lower the AFM head until the sample surface comes into focus in the optical view. Be careful not to crash the probe into the sample surface, as this could result in probe and/or sample damage.
NOTE: The AFM control software used here provides two focusing options: Sample (default) and Tip Reflection. The default option employs a 1 mm focal length, meaning the AFM cantilever will be ~1 mm above the surface when the surface appears in focus in the optical view. Tip Reflection mode uses a 2 mm focal length, so the surface will appear in focus when the AFM cantilever is ~2 mm above the surface, while the tip reflection will appear in focus when the cantilever is ~1 mm above the surface (in the case of a reflective sample surface). The suggested method for approaching the surface is to begin in Tip Reflection mode and approach at full speed (100%) until the sample surface comes into focus, then switch to Sample (default) and approach at medium speed (20%) until the surface again comes into focus.

4. Topography imaging (main line)

NOTE: The protocol described below assumes the use of intermittent contact (tapping) mode for topography imaging.

Perform a cantilever tune by choosing start and end frequencies that will sweep the dither piezo drive frequency across a region chosen to span the expected resonance frequency of the selected probe (e.g., 50-100 kHz for a probe with nominal f₀ = 75 kHz).
Depending on the particular AFM system and software employed (see Table of Materials), utilize a single-click auto tune feature to automate the steps below based on the known nominal values for the chosen probe type.
NOTE: Tuning the cantilever involves identifying its natural resonance frequency and adjusting the drive amplitude (at or near that frequency) so the cantilever oscillates at an appropriate target amplitude (in nanometers).
1. Choose a drive frequency for the main line cantilever tune that is offset to slightly lower frequency than the resonance peak (~5% decrease in amplitude from the peak) to compensate for shifts in the resonance frequency due to changing tip-sample interactions during tip-sample approach.
2. Choose a drive amplitude that results in a target amplitude corresponding to ~50 nm cantilever oscillation (~500 mV amplitude on the PSD for the AFM system and MFM probe employed here, see Table of Materials) as a good starting point.
  NOTE: To convert the measured photodiode deflection signal (in mV or V) into an oscillation amplitude (in nm) requires knowledge of the nominal or measured probe deflection sensitivity.
3. Choose an amplitude setpoint corresponding to ~0.8x of the free space target amplitude (i.e., ~40 nm for a free space amplitude of 50 nm) as a good starting point for topography imaging.
  NOTE: A higher amplitude setpoint will result in a gentler engage but will increase the likelihood of a false engage (i.e., the instrument/software mistakenly thinking the probe is engaged on the surface due to a slight decrease in oscillation amplitude arising from random fluctuations/transient forces acting on the cantilever). Conversely, a lower amplitude setpoint decreases the probability of a false engage, but at the expense of potentially increased tip wear or sample damage upon engaging.
Engage on the sample surface and set the desired scan size depending upon the sample and features of interest (typically somewhere between <1 µm to tens of µm in X and Y).
Increase the amplitude setpoint in increments of 1-2 nm until the tip just loses contact with the sample surface, as seen by the trace and retrace lines failing to track each other in the height sensor channel. Then, decrease the amplitude setpoint by ~2-4 nm so the tip is just in contact with the sample surface.
NOTE: The above will help to minimize the tip-sample interaction force, thereby preserving the sample, lengthening the probe tip life, and improving MFM performance by minimizing tip wear, in particular premature loss of the magnetic coating, as well as the possibility of introducing tip artifacts into the topography and/or magnetic phase images.
Optimize the proportional (P) and integral (I) gains by adjusting them so they are high enough to force the feedback system to track the sample surface topography while minimizing noise. To do this, increase the gains until noise just begins to appear in the error channel, then back off slightly. The system is typically more sensitive to the I gain than the P gain.

5. MFM imaging (interleaved lift mode pass)

Once the AFM topography imaging parameters have been optimized, withdraw a short distance (≥200 nm) from the surface and return to the probe tuning menu. Perform a second cantilever tune to be used to acquire the interleaved lift mode MFM line, making sure to unlink the results of this tune from the previous main line parameters.
1. In contrast to the 5% peak offset employed for the main (topography) line tune in Step 4.2.1, for the interleaved lift mode (MFM) tune, set the peak offset to 0% (i.e., drive the probe at its natural free space resonance frequency during the interleaved MFM pass, since the probe will be oscillating outside the region where strongly attractive or repulsive van der Waals electrostatic forces are felt). Choose start and end frequencies that will sweep the drive frequency across a region spanning the resonance frequency of the probe, similar to step 4.1.
2. Adjust the interleaved lift mode target (or drive) amplitude to be slightly less than the main line target (or drive) amplitude chosen in step 4.2.2 (e.g., ~45 nm target amplitude for the interleaved lift mode MFM pass if using a 50 nm target amplitude for the topography main line). This will enable high sensitivity MFM imaging without striking the surface (i.e., generating topographical artifacts or phase spikes) when utilizing low lift heights for optimal lateral resolution.
Leave the cantilever tune window, reengage on the surface, and optimize the MFM imaging parameters.
1. Set the initial lift scan (interleaved MFM pass) height to 25 nm, then gradually decrease in increments of ~2-5 nm. Once the probe begins to just strike the surface, sharp spikes will appear in the MFM phase channel; immediately increase the scan height by ~2-5 nm to preserve the probe tip and prevent introduction of topographical artifacts.
2. Increase the interleave drive amplitude in small increments corresponding to ~2-5 nm in interleave oscillation amplitude until the interleave drive amplitude exceeds the mainline drive amplitude, or the probe begins to contact the surface as evidenced by spikes in the MFM phase channel. Then, decrease the interleave drive amplitude slightly (corresponding to ~1-2 nm increments) so that no spikes are seen in the MFM phase channel.
3. Continue iteratively optimizing the lift scan height and interleave drive amplitude by adjusting in progressively smaller increments until a high-resolution MFM image free of topographical artifacts is obtained.
  1. Because the tip-sample van der Waals interactions responsible for topography artifacts drop off much more rapidly with distance than the desired long-range magnetic forces, to evaluate the origin of features in the MFM magnetic phase image, investigate the lift height dependence of these features. Topography artifacts will tend to disappear (appear) abruptly with small increases (decreases) in lift height, whereas true magnetic phase responses will change gradually (e.g., resolution and signal to noise will improve with decreasing lift height).
  2. Likewise, if changes are observed in the magnetic moment alignment of low coercivity samples upon repeated scanning, this may be indicative of tip-induced switching that will necessitate the use of a low moment probe (see Table of Materials) and potentially higher lift heights as well.

Representative Results

Artificial spin-ice (ASI) lattices
Artificial spin ices are lithographically defined two-dimensional networks of interacting nanomagnets. They exhibit frustration by design (i.e., the existence of many local minima in the energy landscape)²¹^,⁴²^,⁴³. High-resolution MFM imaging to elucidate the magnetic configurations and interactions between the array components offers the unique opportunity to better understand the spin-ice state of the lattice²¹. Spin-ice lattices for MFM imaging were prepared via electron-beam lithography on a coplanar wave guide (CPW) consisting of 10 nm thick titanium (Ti) and 150 nm thick gold (Au) deposited on a silicon wafer (Figure 1A). The ASIs were composed of 20 nm thick CoFe (Co₉₀Fe₁₀) and/or Py (Ni₈₀Fe₂₀) patterned to form ~260 nm x ~80 nm nanoscale bar magnets arranged in both single (i.e., only CoFe or Py) and bicomponent (i.e., CoFe and Py) square²⁸ and hexagonal (honeycomb)⁴⁴ arrays. The resultant arrays of nanoscale bar magnets were imaged via scanning electron microscopy (SEM), with SEM images of exemplar single component (CoFe only) square and hexagonal arrays shown in Figure 1B. Although there is significant interest within the ASI research community regarding ASI ground states, for the samples investigated here an external magnetic field was applied along the long axis of the CPW after fabrication, resulting in an in-plane orientation of the ASI magnetic moments. Figure 1C shows the 16 possible moment configurations of a square ASI lattice, as well as the eight possible moment configurations of a honeycomb ASI lattice. High-resolution glovebox MFM as described in the protocol was then used to image both single and bicomponent square and hexagonal ASI lattices.

Figure 2 presents instructive AFM topography and MFM magnetic phase images of representative square and hexagonal lattice arrays obtained in an inert atmosphere glovebox before fully optimizing MFM imaging parameters. Examination of the topography images in Figure 2A and Figure 2D shows a shadowing effect on the left side of the vertical lattice members that is indicative of a tip artifact (double tip). The streaks seen in the corresponding MFM phase images in Figure 2B (slight) and Figure 2E (more pronounced) are the result of phase jumps or offsets, likely due to the probe striking the sample surface during the lift mode pass (i.e., topographical interference due to slightly too low a lift height or too large an oscillation amplitude in the interleaved lift mode pass). Conversely, the speckled, fuzzier nature of the phase image in Figure 2H is due to decreased signal to noise (i.e., sensitivity) arising from the reverse problem of too high a lift height or too small an oscillation amplitude in the interleaved lift mode pass relative to the optimal values. Nevertheless, despite these issues in terms of suboptimal image quality, the overlays of the MFM magnetic phase data on the 3D topographies of the three lattices show that, relative to the schematics shown in Figure 1C, the square arrays, whose ground state is a type I configuration, adopt a type II configuration following application of the external magnetic field (aligned along the vertical axis in Figure 2C,F)²⁶^,²⁷. Meanwhile, the hexagonal array adopts a type I configuration (external magnetic field was applied along the horizontal axis in Figure 2F,I)²⁶. Additionally, in Figure 2C, the magnetic phase contrast is noticeably stronger for the horizontal (CoFe) lattice components than for the vertical (Py) components. In Figure 2F, the ASI composition is reversed (i.e., the vertical lattices are composed of CoFe, while the horizontal lattices are Py), and likewise the magnetic phase contrast is reversed, as it is now the vertical (CoFe) lattice components that show the greater contrast. These two bicomponent square ASIs were located adjacent to each other on the same CPW and imaged one after the other, with the same probe and imaging conditions. Thus, the heightened magnetic phase contrast seen in both images for the CoFe component relative to the Py component is indicative of CoFe's larger magnetic dipole moment.

As alluded above, perhaps the easiest mistake to make in attempting to obtain high-resolution MFM images is employing too low a lift scan height, or alternatively, too high a drive amplitude for the chosen lift height. This results in topographic crosstalk or interference in the magnetic phase channel. An extreme example of this is shown in Figure 3, where the phase images (Figure 3B,D) look strikingly similar to the corresponding sample topography images (Figure 3A,C). In the case of Figure 3A,B, a lift height of 11 nm was used, and the interleave drive amplitude was greater (680 mV) than the main line topography drive amplitude (640 mV), leading to the probe simply mapping the sample topography rather than the desired magnetic phase during the lift mode pass. In Figure 3C,D, a slightly higher lift height was employed (12 nm), and the interleave drive amplitude (686 mV) was decreased to be slightly lower than the main line topography drive amplitude (700 mV). As a result, although the phase image in Figure 3D still shows clear evidence of topography artifacts (i.e., phase shifts arising from tip-sample van der Waals interactions), it also contains intermingled actual magnetic phase response at the hexagonal ASI lattice array junctions. However, the magnetic phase image in Figure 3D is not a reliable indicator of the true magnetic moment orientation of the individual ASI array elements because of co-mingling of topography response due to the oscillation amplitude still being too large for the low lift height employed. Figure 3D serves as a stark visual reminder that users must exercise extreme caution in interpreting MFM magnetic phase images when operating with low lift heights, and always confirm there is no topographic interference causing artifacts in the magnetic phase image (see final Note in the Protocol).

Despite the examples to the contrary in Figure 3, following the procedure described in the Protocol, lift heights as low as 10 nm were routinely achieved on these ASI samples in the glovebox with no topographic interference. To aid the reader, Figure 4 displays a progression of images of a single component (Py only) square ASI lattice obtained while optimizing the MFM imaging parameters, with Figure 5 showing the final, optimized image of that ASI. Figure 4A,B is reminiscent of Figure 2H, with too high a lift height (Figure 4A) and/or too small a drive/oscillation amplitude in the lift mode pass (Figure 4A,B) for optimal sensitivity and resolution. Conversely, the magnetic phase image seen in Figure 4C is extremely crisp, with a lift height of 10 nm and a lift mode drive amplitude only slightly less than the main line topography drive amplitude; however, it is starting to show slight evidence of topographical artifacts along the array component boundaries (white ovals). Thus, by slightly decreasing the lift mode drive amplitude, the optimized MFM images presented in Figure 4D and Figure 5 are obtained, with topographical interference in the MFM magnetic phase avoided.

Magnetic shape memory alloy (MSMA)
When grown as a highly pure single crystal, Ni-Mn-Ga is a prototypical MSMA³⁴. Ni-Mn-Ga crystals typically contain numerous twin boundaries, occurring wherever two twin domains meet, with surface relief indicating the location of the twin boundaries and the magnetization direction and crystallographic orientation changing between adjacent twin domains¹⁶. Consequently, MFM can be used to image twin boundaries and track their movement in response to an applied magnetic field or force³⁶^,⁴⁵. Figure 6 displays the magnetic phase image of a polished single crystal Ni-Mn-Ga sample (Figure 6A), as well as the magnetic phase image overlaid as a colored skin on top of the sample's 3D topography (Figure 6C). The images clearly display how and where the twin boundaries line up with the magnetic orientation; Figure 6A shows the characteristic stair step magnetic orientation across the twin boundaries, while Figure 6C shows the long direction of the magnetic domains switching at the topographical features (i.e., extended diagonal ridges and valleys running from lower left to upper right of the images) indicative of the twin boundaries⁴⁶. As with the ASI images, the Ni-Mn-Ga MFM image(s) were acquired in an inert atmospheric glovebox to help eliminate the presence of surface water due to ambient humidity and thereby enable low lift heights (15 nm in the case of the images shown in Figure 6), for increased resolution and sensitivity to resolve the ~200 nm wide magnetic domains seen throughout Figure 6A and in the Figure 6B zoom acquired in the central region of the image indicated by the blue square in Figure 6A.

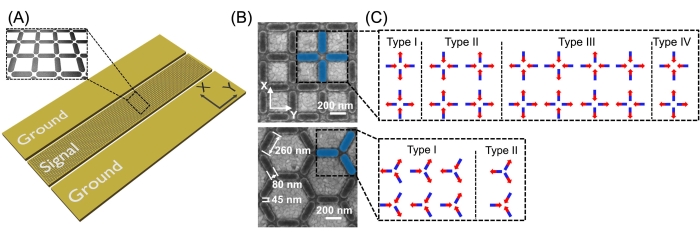
Figure 1: Square and honeycomb artificial spin-ice networks. (A) Schematic of the experimental configuration. Extended artificial spin-ice (ASI) networks are patterned on the top of the signal line of a coplanar waveguide made of Ti/Au via electron-beam lithography. The inset shows a magnified image of a square ASI structure. The bias of the applied external magnetic field is oriented along the long side (Y-direction) of the coplanar waveguide. (B) Scanning electron micrographs of representative square and honeycomb ASI lattices (CoFe only) with the dimensions of the elements. (C) Schematic depicting the 16 possible moment configurations of a square artificial spin-ice lattice and eight possible moment configurations of a honeycomb artificial spin-ice lattice. Please click here to view a larger version of this figure.

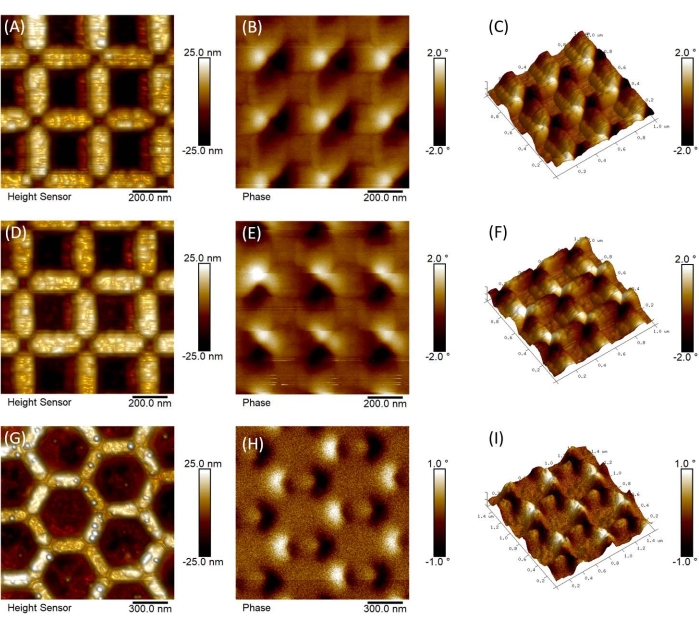
Figure 2: MFM imaging of magnetic moment configurations in ASI networks. AFM topography (left column; A,D,G) and corresponding MFM magnetic phase images (middle column; B,E,H) of representative bicomponent (CoFe and Py) square (top and middle rows; A–F), and single component (CoFe only) hexagonal (bottom row; G–I) ASI lattice arrays prior to full optimization of MFM imaging parameters. The right column (C,F,I) displays the 3D AFM topography of each ASI sample with the corresponding MFM phase channel overlaid as a colored skin to show the relative alignment of the magnetic dipole moments within the ASI structures. Following application of an external magnetic field, the square lattice ASIs adopt a type II configuration (field applied along the vertical axis, corresponding to the Py elements in A-C and the CoFe elements in D-F), whereas the hexagonal lattice (field applied along the horizontal axis in this image) adopts a type I arrangement (see Figure 1C). Please click here to view a larger version of this figure.

Figure 3: Topographical artifacts in MFM magnetic phase images. Representative AFM topography (left column; A,C) and MFM magnetic phase (right column; B,D) images of a single component (Py only) square ASI (top; A-B) and bicomponent (CoFe = vertical elements; Py = oblique elements) honeycomb ASI (bottom; C-D) showing clear evidence of topographic artifacts in the MFM magnetic phase images. (A) Drive amplitude = 640 mV, (B) Lift height = 11 nm, Drive amplitude = 680 mV, (C) Drive amplitude = 700 mV, (D) Lift height = 12 nm, Drive amplitude = 686 mV. Please click here to view a larger version of this figure.

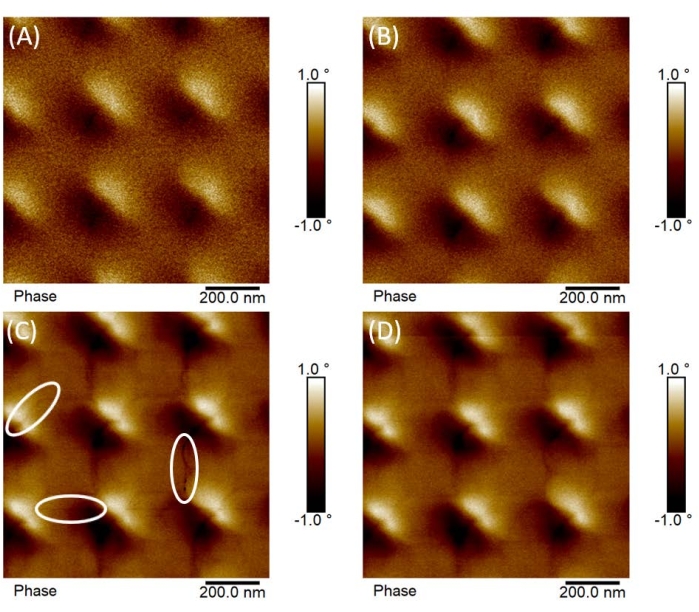
Figure 4: Progression in MFM phase image quality with parameter optimization. Progression in MFM phase image quality for a single component (Py only) square ASI lattice array as the MFM imaging parameters are sequentially/iteratively optimized: (A) Lift scan height = 15 nm, Drive amplitude = 80 mV; (B) Lift scan height = 10 nm, Drive amplitude = 110 mV; (C) Lift scan height = 10 nm, Drive amplitude = 240 mV; (D) Lift scan height = 10 nm, Drive amplitude = 220 mV. For reference, the main (topography) line drive amplitude was held constant at 250 mV, corresponding to ~50 nm free space amplitude, for all images. As indicated by the white ovals, image (C) shows evidence of slight topographical artifacts beginning to appear in the phase image (dark lines emanating from the array junctions along the edges of the nanomagnets), indicating the lift scan height is too low or interleave mode amplitude is too high. By slightly decreasing the interleave amplitude in (D), the topographical artifacts virtually disappear without noticeably sacrificing image quality. Please click here to view a larger version of this figure.

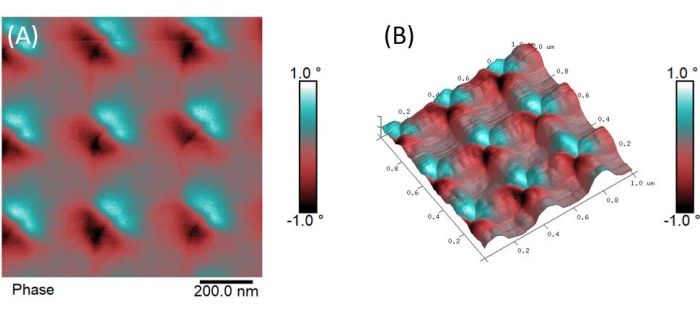
Figure 5: Fully optimized MFM magnetic phase image. Fully optimized MFM magnetic phase images of the representative single component (Py only) square ASI lattice array in Figure 4. (A) 2D magnetic phase image. (B) 3D topography with magnetic phase overlaid as a colored skin showing the ASI exhibits a type II configuration (see Figure 1C) following application of an external magnetic field along the vertical axis. Please click here to view a larger version of this figure.

Figure 6: MFM imaging of magnetic twin boundaries in a single crystal Ni-Mn-Ga sample. (A) 45 µm x 45 µm MFM magnetic phase image of a single crystal Ni-Mn-Ga sample with diagonal twins' present exhibiting the expected ~90° stair step magnetic orientation pattern across the twin boundaries. (B) Zoomed higher resolution (pixel density) MFM magnetic phase image acquired of the 10 µm x 10 µm region indicated by the white square in (A) showing the alternating magnetic domains are ~200 nm wide. (C) MFM magnetic phase image from (A) overlaid as a colored skin atop the 3D sample topography, showing that magnetization direction switching occurs at the twin boundaries as evidenced by its alignment with the topographical surface relief features seen running from lower left to upper right at ~45° with respect to the scan direction/image. Please click here to view a larger version of this figure.

Supplementary Figure S1. Probe holder mounting block with three probe mounting stations. Please click here to download this File.

Supplementary Figure S2. Schematic of the standard probe holder for the Dimension series' AFM heads. Please click here to download this File.

Supplementary Figure S3. Magnetizing a MFM probe. (A) The magnet removed from its case and being placed on the probe. (B) The magnet after being place on the probe. Please click here to download this File.

Supplementary File 1. A general standard operating protocol for using magnetic force microscopy (MFM). Please click here to download this File.

Discussion

High-resolution MFM imaging requires that a corresponding high-resolution, high-fidelity topography scan first be acquired for each line. This topography scan is typically obtained through intermittent contact or tapping mode AFM, which employs an amplitude modulation feedback system to image sample topography⁴⁷. The fidelity of the topography scan can be optimized by adjusting the amplitude set point of the cantilever and feedback gains as described in the Protocol. The amplitude setpoint is critical, as it controls the degree of interaction between the probe tip and the sample surface. Too low a setpoint often leads to damage of the sample surface and/or probe tip, which can lead to deleterious effects on the interleaved MFM line if the magnetic coating is removed; too high an amplitude setpoint can lead to poor phase image contrast⁴⁸. Likewise, the proportional and integral gains are also important considerations in minimizing steady-state error and effectively improving the system response⁴⁹.

During the interleaved lift mode MFM pass after acquisition of each topography line, the MFM probe will experience a varying degree of unwanted short-range van der Waals interactions, which are responsible for generating the sample topography image, versus desirable longer-range magnetic force interactions (to generate the MFM image) depending on the tip-sample separation distance¹. Empirically determining the boundary of the van der Waals dominated regime is perhaps the most important factor in obtaining high-resolution, artifact-free MFM images, as shown in Figure 3 and Figure 4. The two key parameters to optimize to reach the approximate boundary between these two regimes (where the highest resolution MFM images will be obtained, as shown in Figure 5) are the lift scan height and drive (and hence target oscillation) amplitude. A good rule of thumb for identifying topographical artifacts is that they will disappear quickly (i.e., abruptly) with a small increase in lift height or decrease in lift mode drive amplitude (see Figure 4C,D and Supplementary File 1). Likewise, changes in the observed magnetic moment alignment of low coercivity samples with repeated scanning at low lift heights may be indicative of tip-induced switching³⁰, necessitating the use of a low moment probe (see Table of Materials) to preserve the sample's magnetic orientation during imaging.

To prevent topographical interference, the lowest achievable lift height will fundamentally be limited by the height of any high aspect ratio features on the sample surface. However, as mentioned previously, the lower the lift height, the greater the achievable resolution; MFM operation in a low water (<0.1 ppm) glovebox environment allows lift heights of 10 nm to be routinely achieved on smooth (nm scale roughness) samples, as a result of decreased screening of the sample and elimination of interfering tip-sample interactions with the surface water layer. To the authors' knowledge, such lift heights are among the lowest reported in any MFM studies¹⁷. However, the likelihood of topographic interference (e.g., as evidenced by abrupt MFM phase jumps or spikes) increases with decreasing lift height, potentially leading to a need to decrease the lift mode drive (and hence oscillation) amplitude, which will negatively impact MFM sensitivity. High sensitivity is necessary for measuring inherently weak or in-plane magnetic moments such as those in the ASI samples shown in Figure 2 and Figure 5, and thus there becomes a point of diminishing returns in decreasing the lift height if a robust oscillation amplitude must be sacrificed to do so. Therefore, it is necessary to iteratively adjust the lift height and drive/oscillation amplitude for the optimal trade-off between MFM resolution and sensitivity for the sample being studied. In the case of the ASI samples, as seen in Figure 5, the appearance of topographic artifacts at extremely low lift heights can be confirmed and controlled through small changes in the drive (oscillation) amplitude (or alternatively, a slight increase in the lift height). Conversely, for the Ni-Mn-Ga MSMA sample presented in Figure 6, the large magnetic contrast between adjacent nanotwin domains means that ultimately decreasing the lift height to maximize resolution is more important than increasing the drive/oscillation amplitude to improve sensitivity.

In conclusion, the techniques described in this study (see Protocol and Supplementary File 1) offer substantial benefits and a roadmap for those considering conducting MFM imaging of nanoscale magnetic domains. In particular, the ability to image in-plane magnetic moments via high-resolution, high-sensitivity MFM can provide significant insight into understanding the magnetic structure of a wide variety of exciting material systems and architectures, including artificial spin ices and magnetic shape memory alloys. Both materials offer a fascinating playground for the future convergence of nanomagnetism, nanomagnonics, and functional devices¹⁷^,⁵⁰^,⁵¹^,⁵². Moreover, the highly degenerate ground state of artificial spin ices has long garnered scientific interest as a model system for collective spin physics and for their potential in complex magnetic ordering and collective disorder, with MFM playing a key role in enabling the discovery and investigation of frustration in ASI²¹. Going forward, understanding magnetic dipole orientation, particularly in response to an applied magnetic field²³, can speed the implementation of ASIs into nanoelectronics and low-energy computing, revolutionizing nanomagnonics and enabling their incorporation into everyday life⁵³. When combined with careful sample preparation and appropriate probe choice, MFM offers the unique opportunity to provide high-resolution images of these materials, fueling next generations of data storage, shape-memory-alloys, computing, and much more.

Divulgations

The authors have nothing to disclose.

Acknowledgements

All AFM/MFM imaging was performed in the Boise State University Surface Science Laboratory (SSL). The glovebox AFM system used in this work was purchased under National Science Foundation Major Research Instrumentation (NSF MRI) Grant Number 1727026, which also provided partial support for PHD, ACP, and OOM. Partial support for OOM was further provided by NSF CAREER Grant Number 1945650. Research at the University of Delaware, including fabrication and electron microscopy characterization of artificial spin-ice structures, was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-SC0020308. The authors thank Drs. Medha Veligatla and Peter Müllner for helpful discussions and preparation of the Ni-Mn-Ga samples shown here, as well as Dr. Corey Efaw and Lance Patten for their contributions to the MFM standard operating procedure including in the Supplementary File 1.

Materials

Atomic force microscope	Bruker	Dimension Icon	Uses Nanoscope control software
Glovebox, inert atmosphere	MBraun	LabMaster Pro MB200B + MB20G gas purification unit	Custom design (leaktight electrical feedthroughs, vibration isolation, acoustical noise and air current minimization, etc.) and depth for use with Bruker Dimension Icon AFM, 3 gloves, argon atmosphere
MFM probe	Bruker	MESP	k = 3 N/m, f₀ = 75 kHz, r = 35 nm, 400 Oe coercivity, 1 x 10^-13 EMU moment. An improved version with tighter specifications, the MESP-V2, is now available. We have also used Bruker's MESP-RC (2x higher resonance frequency than the standard MESP, f₀ = 150 kHz, with a marginally stiffer nominal spring constant of 5 N/m) and other MESP variants designed for low (0.3 x 10^-13 EMU) or high (3 x 10^-13 EMU) moment (i.e., MESP-LM or MESP-HM, respectively) or coercivity. A variety pack of 10 probes containing 4x regular MESP, 3x MESP-LM, and 3x MESP-HM variants is available from Bruker as MESPSP. Other vendors also manufacture MFM probes with specifications similar to the MESP (e.g., PPP-MFMR from Nanosensors, also available in a variety of variants, including -LC for low coercivity, -LM for low moment, and SSS for "super sharp" decreased tip radius; MAGT from AppNano, available in low moment [-LM] and high moment [-HM] variants). Similarly, Team Nanotec offers a line of high resolution MFM probes (HR-MFM) with several options in terms of cantilever spring constant and magnetic coating thickness.
MFM test sample	Bruker	MFMSAMPLE	Section of magnetic recording tape mounted on a 12 mm diameter steel puck; useful for troubleshooting and ensuring the MFM probe is magnetized and functioning properly
Nanscope Analysis	Bruker	Version 2.0	Free AFM image processing and analysis software package, but proprietary, designed for, and limited to Bruker AFMs; similar functionality is available from free, platform-independent AFM image processing and analysis software packages such as Gwyddion, WSxM, and others
Probe holder	Bruker	DAFMCH or DCHNM	Specific to the particular AFM used; DAFMCH is the standard contact and tapping mode probe holder, suitable for most MFM applications, while DCHNM is a special nonmagnet version for particularly sensitive MFM imaging
Probe magnetizer	Bruker	DMFM-START	MFM "starter kit" designed specifically for the Dimension Icon AFM; includes 1 box of 10 MESP probes (see above), a probe magnetizer (vertically aligned, ~2,000 Oe magnet in a mount designed to accommodate the DAFMCH or DCHNM probe holder, above), and a magnetic tape sample (MFMSAMPLE, above)
Sample Puck	Ted Pella	16218	Product number is for 15 mm diameter stainless steel sample puck. Also available in 6 mm, 10 mm, 12 mm, and 20 mm diameters at https://www.tedpella.com/AFM_html/AFM.aspx#anchor842459
Scanning electron microscope (SEM)	Zeiss Merlin	Gemini II	SEM parameters: 5 keV accelaration voltage, 30 pA electron current, 5 mm working distance. Due to nm scale ASI lattice features, the aperture and stigmation alignment were adjusted before acquisition to produce high quality images.

References

Martin, Y., Wickramasinghe, H. K. Magnetic imaging by ”force microscopy” with 1000 Å resolution. Applied Physics Letters. 50 (20), 1455-1457 (1987).
Grütter, P., Mamin, H. J., Rugar, D., Wiesendanger, R., Guntherodt, H. -. J. . Scanning Tunneling Microscopy II: Further Applications and Related Scanning Techniques. , 151-207 (1992).
Hartmann, U. Magnetic force microscopy. Annual Review of Materials Science. 29 (1), 53-87 (1999).
Abelmann, L., vanden Bos, A., Lodder, C., Hopster, H., Oepen, H. P. . Magnetic Microscopy of Nanostructures. , 253-283 (2005).
Abelmann, L., Lindon, J. C., Tranter, G. E., Koppenaal, D. W. . Encyclopedia of Spectroscopy and Spectrometry (Third Edition). , 675-684 (2017).
Binnig, G., Quate, C. F., Gerber, C. Atomic force microscope. Physical Review Letters. 56 (9), 930-933 (1986).
Eaton, P., West, P. . Atomic Force Microscopy. , (2010).
Garcia, R. Nanomechanical mapping of soft materials with the atomic force microscope: methods, theory and applications. Chemical Society Reviews. 49 (16), 5850-5884 (2020).
Zhang, H., et al. Atomic force microscopy for two-dimensional materials: A tutorial review. Optics Communications. 406, 3-17 (2018).
Jagtap, R., Ambre, A. Overview literature on atomic force microscopy (AFM): Basics and its important applications for polymer characterization. Indian Journal of Engineering & Materials Sciences. 13, 368-384 (2006).
Rugar, D., et al. Magnetic force microscopy: General principles and application to longitudinal recording media. Journal of Applied Physics. 68 (3), 1169-1183 (1990).
Ladak, S., Read, D., Perkins, G., Cohen, L., Branford, W. Direct observation of magnetic monopole defects in an artificial spin-ice system. Nature Physics. 6 (5), 359-363 (2010).
Porro, J., Bedoya-Pinto, A., Berger, A., Vavassori, P. Exploring thermally induced states in square artificial spin-ice arrays. New Journal of Physics. 15 (5), 055012 (2013).
Davis, P. H., et al. Localized deformation in Ni-Mn-Ga single crystals. Journal of Applied Physics. 123 (21), 215102 (2018).
Reinhold, M., Kiener, D., Knowlton, W. B., Dehm, G., Müllner, P. Deformation twinning in Ni-Mn-Ga micropillars with 10M martensite. Journal of Applied Physics. 106 (5), 053906 (2009).
Reinhold, M., Watson, C., Knowlton, W. B., Müllner, P. Transformation twinning of Ni-Mn-Ga characterized with temperature-controlled atomic force microscopy. Journal of Applied Physics. 107 (11), 113501 (2010).
Watson, C. S., Hollar, C., Anderson, K., Knowlton, W. B., Müllner, P. Magnetomechanical four-state memory. Advanced Functional Materials. 23 (32), 3995-4001 (2013).
Al-Khafaji, M. A., Rainforth, W. M., Gibbs, M. R. J., Bishop, J. E. L., Davies, H. A. The effect of tip type and scan height on magnetic domain images obtained by MFM. IEEE Transactions on Magnetics. 32 (5), 4138-4140 (1996).
Kaffash, M. T., Lendinez, S., Jungfleisch, M. B. Nanomagnonics with artificial spin ice. Physics Letters A. 402, 127364 (2021).
Skjærvø, S. H., Marrows, C. H., Stamps, R. L., Heyderman, L. J. Advances in artificial spin ice. Nature Reviews Physics. 2 (1), 13-28 (2020).
Wang, R., et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature. 439 (7074), 303-306 (2006).
Lendinez, S., Jungfleisch, M. B. Magnetization dynamics in artificial spin ice. Journal of Physics: Condensed Matter. 32 (1), 013001 (2019).
May, A., et al. Magnetic charge propagation upon a 3D artificial spin-ice. Nature Communications. 12 (1), 3217 (2021).
Gliga, S., Iacocca, E., Heinonen, O. G. Dynamics of reconfigurable artificial spin ice: Toward magnonic functional materials. APL Materials. 8 (4), 040911 (2020).
Sklenar, J., Lendinez, S., Jungfleisch, M. B., Stamps, R. L., Schultheiß, H. . Solid State Physics. 70, 171-235 (2019).
Nisoli, C., Moessner, R., Schiffer, P. Colloquium: Artificial spin ice: Designing and imaging magnetic frustration. Reviews of Modern Physics. 85 (4), 1473 (2013).
Zhang, X., et al. Understanding thermal annealing of artificial spin ice. APL Materials. 7 (11), 111112 (2019).
Lendinez, S., Kaffash, M. T., Jungfleisch, M. B. Emergent spin dynamics enabled by lattice interactions in a bicomponent artificial spin ice. Nano Letters. 21 (5), 1921-1927 (2021).
Goryca, M., et al. Magnetic-field-dependent thermodynamic properties of square and quadrupolar artificial spin ice. Physical Review B. 105 (9), 094406 (2022).
Gartside, J. C., et al. Realization of ground state in artificial kagome spin ice via topological defect-driven magnetic writing. Nature Nanotechnology. 13 (1), 53-58 (2018).
Straka, L., Fekete, L., Heczko, O. Antiphase boundaries in bulk Ni-Mn-Ga Heusler alloy observed by magnetic force microscopy. Applied Physics Letters. 113 (17), 172901 (2018).
Straka, L., Fekete, L., Rameš, M., Belas, E., Heczko, O. Magnetic coercivity control by heat treatment in Heusler Ni-Mn-Ga (-B) single crystals. Acta Materialia. 169, 109-121 (2019).
Sozinov, A., Lanska, N., Soroka, A., Zou, W. 12% magnetic field-induced strain in Ni-Mn-Ga-based non-modulated martensite. Applied Physics Letters. 102 (2), 021902 (2013).
Ullakko, K., Huang, J., Kantner, C., O’Handley, R., Kokorin, V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Applied Physics Letters. 69 (13), 1966-1968 (1996).
Heczko, O. Magnetic shape memory effect and highly mobile twin boundaries. Materials Science and Technology. 30 (13), 1559-1578 (2014).
Niklasch, D., Maier, H., Karaman, I. Design and application of a mechanical load frame for in situ investigation of ferromagnetic shape memory alloys by magnetic force microscopy. Review of Scientific Instruments. 79 (11), 113701 (2008).
Wu, A. Q., et al. HAMR areal density demonstration of 1+ Tbpsi on spinstand. IEEE Transactions on Magnetics. 49 (2), 779-782 (2013).
Sifford, J., Walsh, K. J., Tong, S., Bao, G., Agarwal, G. Indirect magnetic force microscopy. Nanoscale Advances. 1 (6), 2348-2355 (2019).
Koblischka, M., Hartmann, U. Recent advances in magnetic force microscopy. Ultramicroscopy. 97 (1-4), 103-112 (2003).
Kief, M., Victora, R. Materials for heat-assisted magnetic recording. MRS Bulletin. 43 (2), 87-92 (2018).
Kautzky, M. C., Blaber, M. G. Materials for heat-assisted magnetic recording heads. MRS Bulletin. 43 (2), 100-105 (2018).
Jungfleisch, M., et al. Dynamic response of an artificial square spin ice. Physical Review B. 93 (10), 100401 (2016).
Heyderman, L. J., Stamps, R. L. Artificial ferroic systems: novel functionality from structure, interactions and dynamics. Journal of Physics: Condensed Matter. 25 (36), 363201 (2013).
Kaffash, M. T., Lendinez, S., Jungfleisch, M. B. Tailoring ferromagnetic resonance in bicomponent artificial spin ices. 2021 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS). , 500-503 (2021).
Lai, Y., et al. Absence of magnetic domain wall motion during magnetic field induced twin boundary motion in bulk magnetic shape memory alloys. Applied Physics Letters. 90 (19), 192504 (2007).
Venkateswaran, S., Nuhfer, N., De Graef, M. Magnetic domain memory in multiferroic Ni2MnGa. Acta Materialia. 55 (16), 5419-5427 (2007).
Garcia, R., San Paulo, A. Attractive and repulsive tip-sample interaction regimes in tapping-mode atomic force microscopy. Physical Review B. 60 (7), 4961 (1999).
Thormann, E., Pettersson, T., Kettle, J., Claesson, P. M. Probing material properties of polymeric surface layers with tapping mode AFM: Which cantilever spring constant, tapping amplitude and amplitude set point gives good image contrast and minimal surface damage. Ultramicroscopy. 110 (4), 313-319 (2010).
Xue, B., Yan, Y., Hu, Z., Zhao, X. Study on effects of scan parameters on the image quality and tip wear in AFM tapping mode. Scanning: The Journal of Scanning Microscopies. 36 (2), 263-269 (2014).
Hon, K., et al. Numerical simulation of artificial spin ice for reservoir computing. Applied Physics Express. 14 (3), 033001 (2021).
Jensen, J. H., Folven, E., Tufte, G. Computation in artificial spin ice. ALIFE 2018: The 2018 Conference on Artificial Life. , 15-22 (2018).
Barker, S., Rhoads, E., Lindquist, P., Vreugdenhil, M., Müllner, P. Magnetic shape memory micropump for submicroliter intracranial drug delivery in rats. Journal of Medical Devices. 10 (4), (2016).
Gartside, J. C., et al. Reconfigurable training and reservoir computing in an artificial spin-vortex ice via spin-wave fingerprinting. Nature Nanotechnology. 17 (5), 406-469 (2022).

Play Video

PDF

DOI

DOWNLOAD MATERIALS LIST

Citer Cet Article

Parker, A. C., Maryon, O. O., Kaffash, M. T., Jungfleisch, M. B., Davis, P. H. Optimizing Magnetic Force Microscopy Resolution and Sensitivity to Visualize Nanoscale Magnetic Domains. J. Vis. Exp. (185), e64180, doi:10.3791/64180 (2022).