RLC Series Circuit: Problem-Solving

Consider an AC generator with a frequency of 50 hertz and a voltage of 120 volts. The AC generator is connected to an RLC series circuit with a 20-ohms resistor, a 0.2-henry inductor, and a 0.05-farad capacitor. Determine the impedance, current amplitude, and phase difference between the generator's current and emf.

To solve the problem, first, determine the known and unknown quantities in the problem. Recalling the reactance equation for the inductor and capacitor and substituting the values, the inductive and capacitive reactance can be determined as follows:

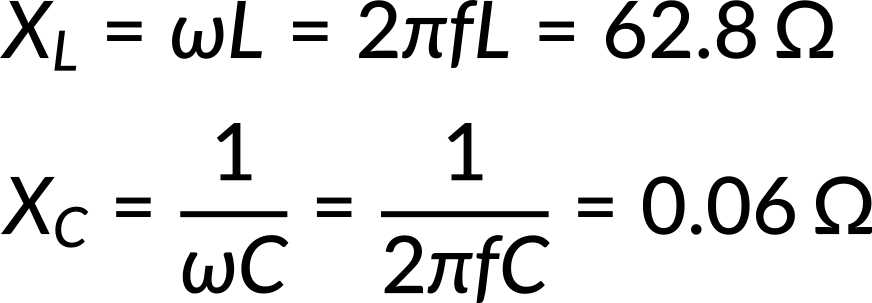
Impedance measures the combined effect of resistance, capacitive, and inductive reactance. Next, recall the impedance equation and substitute the resistance, inductive reactance, and capacitive reactance. By simplifying the equation, the impedance in the circuit can be determined as follows: 

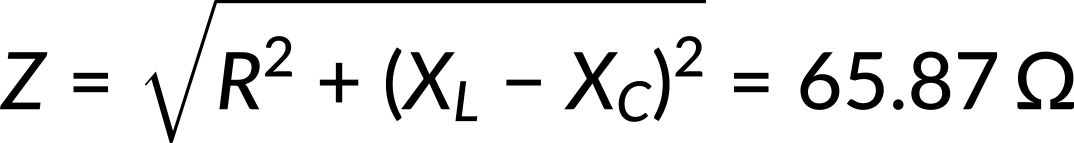
The current's amplitude is the ratio of the voltage's amplitude to the circuit's impedance. Thus, by substituting the known values, the current amplitude can be calculated as follows:

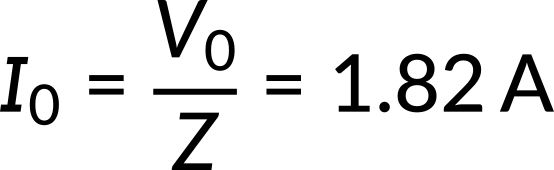
Lastly, recall the phase angle equation in the RLC circuit. By substituting the resistance and reactance values, the phase difference between the current and the emf of the generator can be calculated as follows:

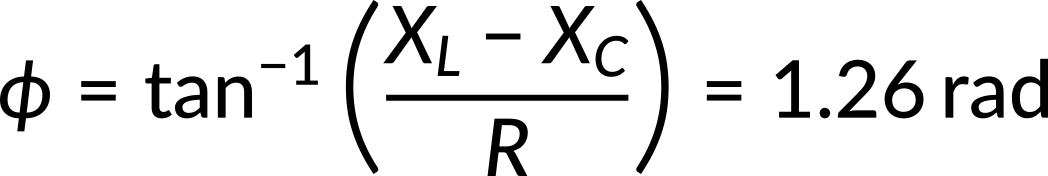
The phase angle is positive because the reactance of the inductor is larger than the reactance of the capacitor.