Magnetic Field Of A Current Loop

Consider a circular loop with a radius a, that carries a current I. The magnetic field due to the current at an arbitrary point P along the axis of the loop can be calculated using the Biot-Savart law.

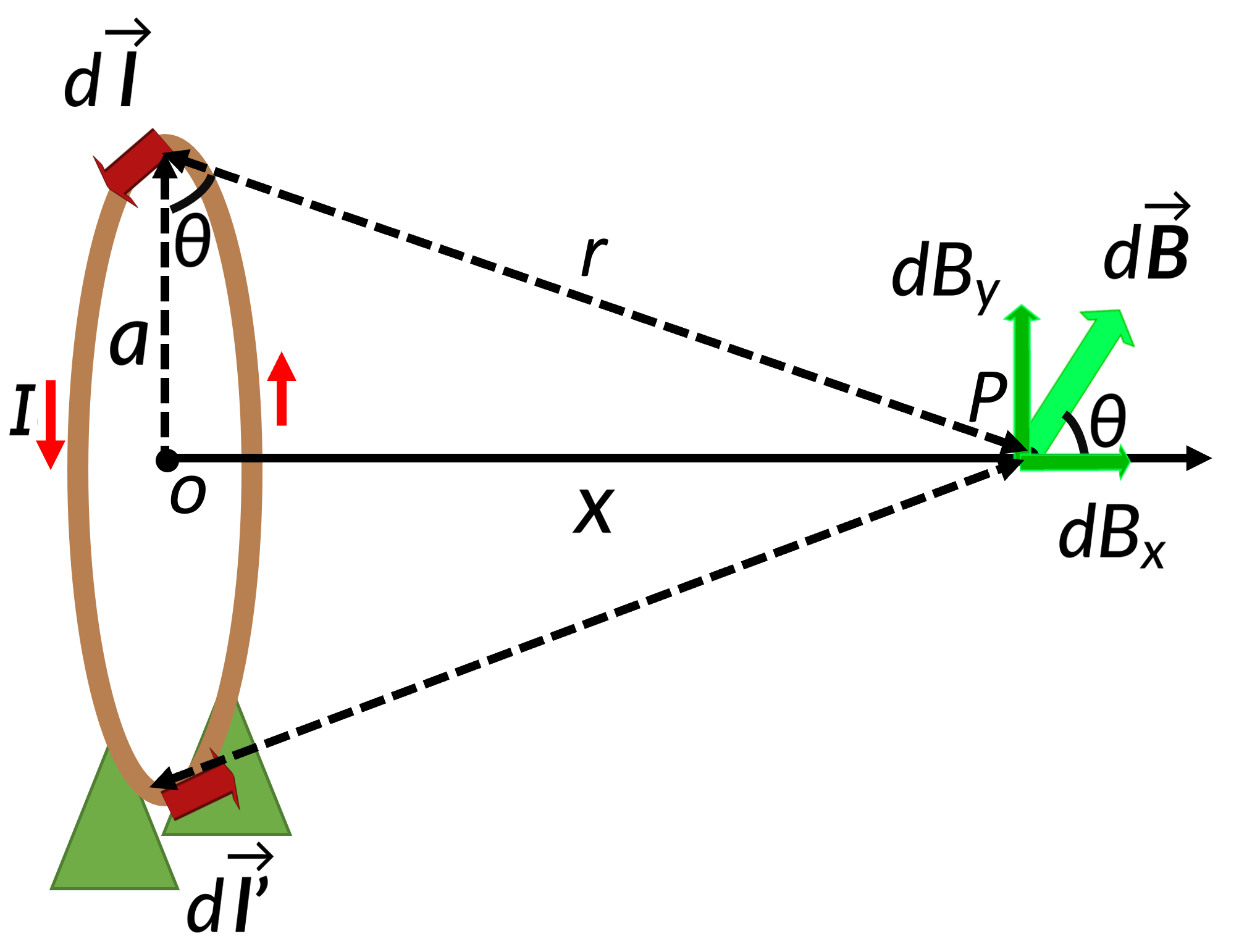
Let axial point P be a distance x from the center of the loop. The magnetic field at P, produced by an infinitesimal current element dl, is directed at an angle θ. The current element and the unit vector along the line joining P are perpendicular at all points on the loop. Substituting this and rewriting r in terms of x and a gives the magnitude of the magnetic field due to the current element.

The magnetic field can be resolved into two components: perpendicular and parallel to the axis. Due to different current elements around the loop, all the perpendicular components of the magnetic field cancel each other. Integrating all the parallel components over all the current elements along the loop, gives the magnetic field on the axis of a circular loop.

For a coil of n closely spaced loops of the same radius, the total field is n times the field due to a single loop.