4.6:
Projectile Motion: Equations
Un abonnement à JoVE est nécessaire pour voir ce contenu. Connectez-vous ou commencez votre essai gratuit.
JoVE Core
Physique
Projectile Motion: Equations
7,612 Views
•
01:26 min
•
April 30, 2023
Projectile motion is commonly observed in our day-to-day life. For example, a basketball thrown by a player, an arrow shot from a bow, and kids jumping into the pool, all undergo projectile motion.
Any projectile motion problem can be solved by using the following strategy:
- Initially, resolve the motion into horizontal and vertical components along the x– and y-axes. The magnitudes of the components of displacement along these axes are x and y. The magnitudes of the vertical and horizontal components of velocity are given by v⋅sin(θ) and v⋅cos(θ), respectively, where v is the magnitude of the velocity and θ is its direction relative to the horizontal.
- Treat the motion as two independent one-dimensional motions: one horizontal and one vertical. Use the kinematic equations for horizontal and vertical motion presented earlier.
- Solve for the unknowns in the two separate motions. Note that the only common variable between the motions is time, t. The problem-solving procedures here are the same as those for one-dimensional kinematics.
- Recombine quantities in the horizontal and vertical directions to find the total displacement and velocity. Finally, solve for the magnitude and direction of the displacement and velocity using
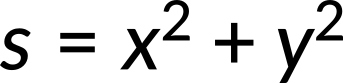
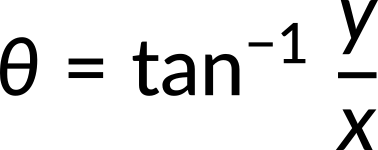
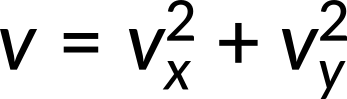
where θ is the direction of the displacement.
This text is adapted from Openstax, University Physics Volume 1, Section 4.3: Projectile Motion.
