31.13:
RLC Circuit as a Damped Oscillator
637 Views
•
•
An RLC circuit combines a resistor, inductor, and capacitor, connected in a series or parallel combination.
Consider a series RLC circuit. Here, the presence of resistance in the circuit leads to energy loss due to joule heating in the resistance. Therefore, the total electromagnetic energy in the circuit is no longer constant and decreases with time. Since the magnitude of charge, current, and potential difference continuously decreases, their oscillations are said to be damped. This is similar to a damped block-spring oscillator, where the amplitude of displacement of the oscillator decreases with time.
The differential equation for damped oscillations in an RLC circuit is given by
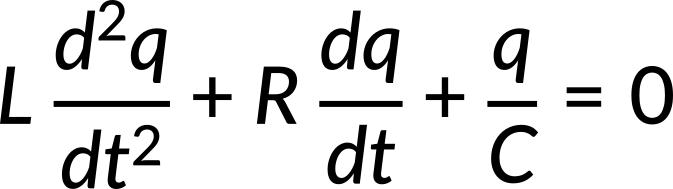
It is known that if the ratio of R/L is less than 1/LC, the circuit becomes an underdamped oscillator. The solution of equation 1 in the case of an underdamped RLC circuit is given by
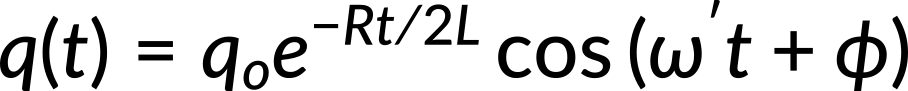
This depicts how the charge on the capacitor oscillates in an underdamped RLC circuit. This solution is the electromagnetic counterpart of the solution for an underdamped spring oscillator that gives the displacement of a damped block-spring oscillator. Analogous to the decrease in displacement amplitude in the block-spring oscillator, the charge oscillates sinusoidally with decreasing amplitude in an underdamped RLC circuit. The angular frequency of the damped oscillations is always less than the angular frequency of the underdamped oscillations.
The energy decay in an underdamped RLC circuit is obtained using the energy relation and is given as
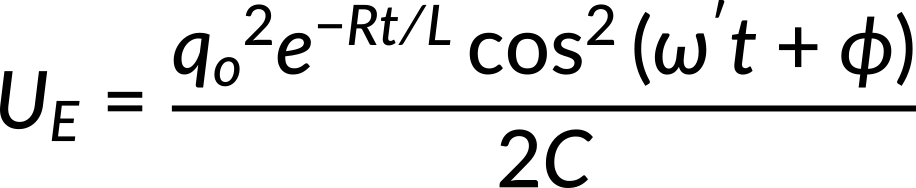
Thus, the energy of the electric field varies sinusoidally, and the amplitude of that oscillation decreases exponentially with time.
