Quantitative Strain Mapping of an Abdominal Aortic Aneurysm
4,538 Views
•
•
概述
Source: Hannah L. Cebull1, Arvin H. Soepriatna1, John J. Boyle2 and Craig J. Goergen1
1Weldon School of Biomedical Engineering, Purdue University, West Lafayette, Indiana
2Mechanical Engineering & Materials Science, Washington University in St. Louis, St Louis, Missouri
The mechanical behavior of soft tissues, such as blood vessels, skin, tendons, and other organs, are strongly influenced by their composition of elastin and collagen, which provide elasticity and strength. The fiber orientation of these proteins depends on the type of soft tissue and can range from a single preferred direction to intricate meshed networks, which can become altered in diseased tissue. Therefore, soft tissues often behave anisotropically on the cellular and organ level, creating a need for three-dimensional characterization. Developing a method for reliably estimating strain fields within complex biological tissues or structures is important to mechanically characterize and understande disease. Strain represents how soft tissue relatively deforms over time, and it can be described mathematically through various estimations.
Acquiring image data over time allows deformation and strain to be estimated. However, all medical imaging modalities contain some amount of noise, which increases the difficulty of accurately estimating in vivo strain. The technique described here successfully overcomes these issues by using a direct deformation estimation (DDE) method to calculate spatially varying 3D strain fields from volumetric image data.
Current strain estimation methods include digital image correlation (DIC) and digital volume correlation. Unfortunately, DIC can only accurately estimate strain from a 2D plane, severely limiting the application of this method. While useful, 2D methods such as DIC have difficulty quantifying strain in regions that undergo 3D deformation. This is because out-of-plane motion creates deformation errors. Digital volume correlation is a more applicable method that divides the initial volume data into regions and finds the most similar region of the deformed volume, thereby reducing out-of-plane error. However, this method proves to be sensitive to noise and requires assumptions about the mechanical properties of the material.
The technique demonstrated here eliminates these issues by using a DDE method, thus making it very useful in the analysis of medical imaging data. Furthermore, it is robust to high or localized strain. Here we describe the acquisition of gated, volumetric 4D ultrasound data, its conversion into an analyzable format, and the use of a custom Matlab code to estimate 3D deformation and corresponding Green-Lagrange strains, a parameter that better describes large deformations. The Green-Lagrange strain tensor is implemented in many 3D strain estimation methods because it allows for F to be calculated from a Least Squares Fit (LSF) of the displacements. The equation below represents the Green-Lagrange strain tensor, E, where F and I represent the deformation gradient and second order identity tensor, respectively.
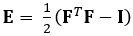 (1)
(1)
Principles
4D ultrasound is a dynamic volume that is acquired utilizing a linearly translating motor attached to an ultrasound transducer, allowing the acquisition of sequential cardiac- and respiratory-gated video loops across a region of interest. This method is useful for visualizing complex structures such as the heart, where hypertrophy or infarction causes unique geometries, or aortic aneurysms, where asymmetric vessel expansion and dissection often occur in tortuous vessels. Additionally, 4D data can provide high-resolution spatial and temporal information, which is also important for cardiovascular imaging.
The DDE method applied to 4D ultrasound data is superior to other methods because it uses non-rigid image registration. Deformation gradient tensors are traditionally estimated from displacement fields following digital volume correlation. In contrast, the DDE method intrinsically estimates deformation gradient tensors during volume registration by optimizing a warping function that is carefully chosen to be directly analogous to the deformation tensor. The warping function depends on both spatial position and the warping parameter (p):
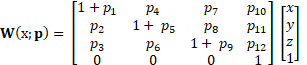 (2)
(2)
The first three elements of this function represent the deformation gradient tensor, F, allowing the calculation of deformation to be directly incorporated into the warping function. This warping method has been proven to increase the accuracy and precision of strain estimation when compared to similar previous techniques because it allows for large or localized deformations commonly found in soft tissues.
Procedure
1. 4D Ultrasound Set-up
- When using the imaging software, use a laptop capable of running mathematical computing software to automate the 4D acquisition process. Connect the laptop with this custom code to the ultrasound system via the USB port. Note that the imaging software has a 4D ultrasound feature integrated into the software.
- After turning on the ultrasound system, set up the physiological monitoring unit while also ensuring that the heart rate and temperature buttons are on. Initialize the 3D motor stage attached to the transducer holder.
- Use the appropriate stage and ultrasound transducer for image acquisition. Ensure that all proper connections are made.
- Proceed with anesthetizing and preparing the animal for imaging. Add ophthalmic ointment to the eyes to prevent corneal desiccation, secure the paws to the stage electrodes, and insert a lubricated rectal temperature probe. Remove fur in the area of interest using a depilatory cream.
- Make sure depilatory cream is completed removed. Then, apply a generous amount of the warmed ultrasonic transducing gel to the animal. This is especially important to create a good connection over the entire region of interest for 4D imaging.
2. 4D Ultrasound Acquisition
- Begin a new study on the ultrasound system and open the imaging window in B-Mode (brightness mode). Lower the transducer onto the animal and locate the region of interest using the x- and y-axis knobs on the stage, making sure the respiratory rate does not decrease substantially. Monitor this at the bottom of the screen.
- Position the transducer within the middle of the region of interest. From there, approximate the distance needed for the transducer to move up and down such that the entire region of interest is included.
- Enter the approximate dimensions into the computing software code, including a step size which is typically ~0.08 mm for abdominal aortic aneurysm imaging. Begin running the code after ensuring the animal's heart and respiratory rates are stable. This is important for reducing errors when reconstructing images.
- After completing the image acquisition, export the data as raw XML files.
3. 4D Ultrasound Data Conversion
- Input the raw XML files into software that can convert the data into the proper format for the 3D stain analysis. Here we use Matlab to convert XML files into MAT files. The full Matlab script is available here.
- For proper conversion, the number of frames, step size, and desired output resolution will also need to be input.
- After resampling the matrix in through plane, import the new MAT file into the 3D strain analysis code.
4. 3D Strain Code Analysis
- Begin analysis by properly adjusting the imported MAT file. For example, the image volume may need to be rescaled to reduce computation time.
- Input the region to be analyzed and determine the appropriate mesh template to segment the image data as either simple boxes or manually chosen polygons. The box size of the regions and spacing between the center points may need to be altered for each data set. The optimal numbers chosen for box size will be around the order of pixels of the feature being tracked, which can be approximated by looking at the number of pixels in two dimensions in one slice. The spacing of the boxes will determine the resolution of the strain fields. More boxes will increase the resolution but may also substantially increase computation time.
- Begin computing the Jacobians and gradients iteratively within each of these regions. After the precomputation is complete, apply the warping function.
- Calculate the deformation gradient tensor. First calculate strain, and then calculate the eigenvalues and eigenvectors using the direct deformation estimation method.
- Plot these results in the desired planes using a technique such as color mapping of a cut plane to represent the strain field over your region of interest.
Three-dimensional strain imaging is used to estimate deformation of soft tissues over time and understand disease. The mechanical behavior of soft tissues, such as skin, blood vessels, tendons, and other organs, is strongly influenced by their extracellular composition, which can become altered from aging and disease. Within complex biological tissues, it is important to characterize these changes, which can significantly affect the mechanical and functional properties of an organ.
Quantitative strain mapping uses volumetric image data and a direct deformation estimation method to calculate the spatially varying three-dimensional strain fields. This video will illustrate the principles of strain mapping, demonstrate how quantitative strain mapping is used to estimate strain fields within complex biological tissues, and discuss other applications.
Biological tissues are strongly influenced by the composition and orientation of elastin and collagen. The protein elastin is a highly elastic component of tissues that continually stretch and contract, such as blood vessels and the lungs. Collagen is the most abundant protein in the body, and is assembled from individual triple-helical polymers that are bundled into larger fibers that provide structural integrity to tissues ranging from skin to bones.
The orientation of these proteins ranges from aligned fibers to fibrous mesh networks, which affects the mechanical properties of the tissue. Strain is a measure of the relative deformation of soft tissues over time, and can be used to visualize injury and disease. It is described and mapped using mathematical estimations.
To map strain in complex organs, such as the heart, four-dimensional ultrasound data, which provides high resolution, spatial, and temporal information, can be used. Then the direct deformation estimation method, or DDE, is applied to the data. A code is used to estimate the 3D deformation and corresponding Green-Lagrange strains using the following equation.
The Green-Lagrange strain tensor depends on the deformation gradient tensor and the second order identity tensor. Deformation gradient tensors are traditionally estimated from displacement fields. In the DDE method, a warping function is optimized to be directly analogous to the deformation tensor. The warping function depends on both spatial position and the warping parameter. The calculation of deformation is directly incorporated into the warping function. The first nine elements represent the deformation gradient tensor.
This method is used to estimate both large and localized deformations in soft tissues. Now that we understand the principles of strain mapping, let’s now see how strain mapping is performed to detect aortic aneurysms in mice.
To begin setup, open the Vivo 2100 software and connect the laptop to the ultrasound system. Make sure the physiological monitoring unit is on to measure heart rate and temperature. Then initialize the 3D motor stage.
Install the ultrasound transducer and ensure that all proper connections are made. Next, anesthetize the animal that will be imaged using 3% isoflurane in a knock-down chamber. Once the mouse is anesthetized, move it to the heated stage and secure a nose cone to deliver 1-2% isoflurane. Apply ophthalmic ointment to the eyes and secure the paws to the stage electrodes to monitor the animal’s respiration and heart rate. Then insert a rectal temperature probe. Apply depilatory cream to remove hair from the area of interest, and then apply a generous amount of warm ultrasound gel to the depilated area.
To start the image acquisition, first, open the imaging window and select B mode. Then lower the transducer onto the animal and use the x and y-axis knobs on the stage to locate the area of interest. Monitor the respiratory rate to make sure it does not decrease substantially. Position the transducer in the middle of the region of interest. Then approximate the distance required to cover the entire region of interest.
Enter these dimensions in the MATLAB code and choose a step size of 0.08 millimeters. Make sure the animal’s heart and respiratory rates are stable, then run the MATLAB code.
After image acquisition, export the data as raw XML files and convert them into MAT files. Make sure to input the number of frames, step size, and output resolution. Then re-sample the matrix in through-plane.
Import the new MAT file into the 3D strain analysis code. It may be necessary to rescale the file to reduce the computation time. Then, input the region to be analyzed. Approximate the number of pixels in a two-dimensional slice of the tracked feature and select the mesh template either as a simple box or manually chosen polygons. Choose the optimal pixel number for the mesh size. Compute the Jacobians and the gradients. Repeat for each region. Then apply the warping function.
Next, using Cartesian deformations calculated from DDE, determine the eigenvalues and eigenvectors of the deformation. Then, select the slices that you want to plot strain values for by scrolling through the long axis, sort axis, and coronal axis views.
Press Select Manifold for Analysis. Then use the cursor to place markers along the aortic wall, including the thrombus, aneurysm, and healthy parts of the aorta. Repeat for all views. Finally, use color mapping to plot the results of the strain field over the region of interest.
Let us have a close look at the example of an angiotensin II-induced suprarenal dissecting abdominal aortic aneurysm acquired from a mouse. First, multiple short axis ECG-gated kilohertz visualization loops are obtained at a given step size along the aorta and combined to create 4D data.
After performing 3D strain calculation using an optimized warping function, the 3D slice visualization plot of the infrarenal aorta is obtained. The color map of principal green strain is overlaid to highlight regions of heterogeneous aortic wall strain. In addition, long axis and short axis views reveal heterogeneous spatial variations in strain, particularly when a thrombus is present.
Corresponding strain plots show higher strain values in healthy regions of the aorta in the long axis, while the aneurysmal region shows decreased strain in the short axis.
Accurate quantitative strain visualization using direct deformation estimation is a useful tool used in various biomedical applications.
For instance, cardiac strain can be quantified. During the cardiac cycle, the myocardium undergoes 3D deformation. Quantifying strain in three dimensions is integral to reliably characterizing the dynamics of this tissue over time. This is useful in tracking disease progression in animal models.
Another application is in the characterization of intestinal tissue. In vivo imaging of the intestines is challenging because of the effects from surrounding structures. However, calculating strain from images of intestinal fibrosis could be particularly useful to provide early detection of problematic areas that require surgical intervention.
At a much smaller scale, this DDE method is also applied to the cellular level by using higher resolution imaging techniques such as confocal microscopy. It serves, for example, in the characterization of extracellular matrix to understand how cells communicate under mechanical changes.
You’ve just watched JoVE’s introduction to quantitative strain visualization. You should now understand how to measure three-dimensional strain in biological tissues and how that is used in early disease detection. Thanks for watching!
Results
Using the procedure described above, 4D ultrasound of an angiotensin II-induced suprarenal dissecting abdominal aortic aneurysm (AAA) of a mouse was acquired. Multiple short-axis EKV video loops were acquired along the aorta and combined to create 4D data, as shown in Figure 1. This data was then converted into a MAT file using a custom code, which was then analyzed in a 3D strain calculation code using a warping function. After optimizing the parameters of the code for a specific data set, a representative, long-axis view with corresponding strain values was produced as well as a 3D slice visualization plot with an overlaid strain color map (Figure 2). This DDE technique and strain data highlight the heterogeneous spatial variations in strain, particularly when a thrombus is present. These results can then be correlated with vessel structure to determine the relationship between in vivo deformation and aneurysm composition.

Figure 1: ECG-gated kilohertz visualization (EKV) loops of the aorta are acquired from manually inputted starting and ending locations, following a step size of 0.2 mm.

Figure 2: 4D high frequency ultrasound data of a murine dissecting abdominal aortic aneurysm represented at systole (A) with principal strain fields estimated and overlaid (B) (Scalebar = 5 mm). Long- and short-axis views representing both aneurysmal and healthy regions corresponding principal strain over one cardiac cycle (systole: t= 0.4) (C, D). These data show relatively high strain levels in healthy regions and reduced strain values within the dissecting aneurysm.
Applications and Summary
Localized in vivo mechanical characterization is an important part of understanding the growth and remodeling of biological tissues. Compared to existing approaches, the strain quantification procedure described here uses an improved method of accurately calculating 3D strain through optimally warping the undeformed image before cross-correlation. This method does not use any material assumptions in determining strains within tissue volumes. Unfortunately, the strain estimation is reliable only down to a kernel size of 15x15x15 voxels when using ultrasound data, suggesting that this DDE approach may not detect subtle features within a strain field. Despite this limitation, it remains an important tool for investigating mechanical responses, diagnosing pathology, and improving disease models.
Many areas of research beyond aortic aneurysms can benefit from this strain measurement tool. Cardiac strain can also be easily quantified using this method. Because the myocardium undergoes 3D deformation during the cardiac cycle, quantifying strain in three dimensions is integral to reliably characterizing the dynamics of this tissue. Reliable strain data is especially important when tracking disease progression in animal models.
3D strain analysis can also be applied to intestinal ultrasound imaging. Mechanical characterization of intestinal tissue is most commonly conducted in vitro. However, this is not always a true representation of the actual behavior of the intestines in vivo because of effects from surrounding structures. As an example of clinically translating this approach, calculating the strain from images of intestinal fibrosis due to abnormal luminal pressure could provide early detection of problematic areas that require surgical intervention.
Beyond the larger scale applications, this method can also be applied to the cellular level by using higher resolution imaging techniques, such as confocal microscopy. Characterizing the extracellular matrix is important for understanding how cells communicate. Much research has been conducted on the biochemical characterization, but understanding how communication can be conducted through mechanical responses requires an understanding of deformation and strain. Bulk strain is not beneficial because there is no way to determine the origin of the deformation change. Applying a high-resolution DDE approach could directly reveal how the extracellular matrix responds to mechanical changes.
ACKNOWLEDGEMENTS
We would like to acknowledge John Boyle, Guy Genin, and Stavros Thomopoulos for the contribution of the DDE custom Matlab code capable of directly estimating Lagrange-Green strain.
成績單
Three-dimensional strain imaging is used to estimate deformation of soft tissues over time and understand disease. The mechanical behavior of soft tissues, such as skin, blood vessels, tendons, and other organs, is strongly influenced by their extracellular composition, which can become altered from aging and disease. Within complex biological tissues, it is important to characterize these changes, which can significantly affect the mechanical and functional properties of an organ.
Quantitative strain mapping uses volumetric image data and a direct deformation estimation method to calculate the spatially varying three-dimensional strain fields. This video will illustrate the principles of strain mapping, demonstrate how quantitative strain mapping is used to estimate strain fields within complex biological tissues, and discuss other applications.
Biological tissues are strongly influenced by the composition and orientation of elastin and collagen. The protein elastin is a highly elastic component of tissues that continually stretch and contract, such as blood vessels and the lungs. Collagen is the most abundant protein in the body, and is assembled from individual triple-helical polymers that are bundled into larger fibers that provide structural integrity to tissues ranging from skin to bones.
The orientation of these proteins ranges from aligned fibers to fibrous mesh networks, which affects the mechanical properties of the tissue. Strain is a measure of the relative deformation of soft tissues over time, and can be used to visualize injury and disease. It is described and mapped using mathematical estimations.
To map strain in complex organs, such as the heart, four-dimensional ultrasound data, which provides high resolution, spatial, and temporal information, can be used. Then the direct deformation estimation method, or DDE, is applied to the data. A code is used to estimate the 3D deformation and corresponding Green-Lagrange strains using the following equation.
The Green-Lagrange strain tensor depends on the deformation gradient tensor and the second order identity tensor. Deformation gradient tensors are traditionally estimated from displacement fields. In the DDE method, a warping function is optimized to be directly analogous to the deformation tensor. The warping function depends on both spatial position and the warping parameter. The calculation of deformation is directly incorporated into the warping function. The first nine elements represent the deformation gradient tensor.
This method is used to estimate both large and localized deformations in soft tissues. Now that we understand the principles of strain mapping, let’s now see how strain mapping is performed to detect aortic aneurysms in mice.
To begin setup, open the Vivo 2100 software and connect the laptop to the ultrasound system. Make sure the physiological monitoring unit is on to measure heart rate and temperature. Then initialize the 3D motor stage.
Install the ultrasound transducer and ensure that all proper connections are made. Next, anesthetize the animal that will be imaged using 3% isoflurane in a knock-down chamber. Once the mouse is anesthetized, move it to the heated stage and secure a nose cone to deliver 1-2% isoflurane. Apply ophthalmic ointment to the eyes and secure the paws to the stage electrodes to monitor the animal’s respiration and heart rate. Then insert a rectal temperature probe. Apply depilatory cream to remove hair from the area of interest, and then apply a generous amount of warm ultrasound gel to the depilated area.
To start the image acquisition, first, open the imaging window and select B mode. Then lower the transducer onto the animal and use the x and y-axis knobs on the stage to locate the area of interest. Monitor the respiratory rate to make sure it does not decrease substantially. Position the transducer in the middle of the region of interest. Then approximate the distance required to cover the entire region of interest.
Enter these dimensions in the MATLAB code and choose a step size of 0.08 millimeters. Make sure the animal’s heart and respiratory rates are stable, then run the MATLAB code.
After image acquisition, export the data as raw XML files and convert them into MAT files. Make sure to input the number of frames, step size, and output resolution. Then re-sample the matrix in through-plane.
Import the new MAT file into the 3D strain analysis code. It may be necessary to rescale the file to reduce the computation time. Then, input the region to be analyzed. Approximate the number of pixels in a two-dimensional slice of the tracked feature and select the mesh template either as a simple box or manually chosen polygons. Choose the optimal pixel number for the mesh size. Compute the Jacobians and the gradients. Repeat for each region. Then apply the warping function.
Next, using Cartesian deformations calculated from DDE, determine the eigenvalues and eigenvectors of the deformation. Then, select the slices that you want to plot strain values for by scrolling through the long axis, sort axis, and coronal axis views.
Press Select Manifold for Analysis. Then use the cursor to place markers along the aortic wall, including the thrombus, aneurysm, and healthy parts of the aorta. Repeat for all views. Finally, use color mapping to plot the results of the strain field over the region of interest.
Let us have a close look at the example of an angiotensin II-induced suprarenal dissecting abdominal aortic aneurysm acquired from a mouse. First, multiple short axis ECG-gated kilohertz visualization loops are obtained at a given step size along the aorta and combined to create 4D data.
After performing 3D strain calculation using an optimized warping function, the 3D slice visualization plot of the infrarenal aorta is obtained. The color map of principal green strain is overlaid to highlight regions of heterogeneous aortic wall strain. In addition, long axis and short axis views reveal heterogeneous spatial variations in strain, particularly when a thrombus is present.
Corresponding strain plots show higher strain values in healthy regions of the aorta in the long axis, while the aneurysmal region shows decreased strain in the short axis.
Accurate quantitative strain visualization using direct deformation estimation is a useful tool used in various biomedical applications.
For instance, cardiac strain can be quantified. During the cardiac cycle, the myocardium undergoes 3D deformation. Quantifying strain in three dimensions is integral to reliably characterizing the dynamics of this tissue over time. This is useful in tracking disease progression in animal models.
Another application is in the characterization of intestinal tissue. In vivo imaging of the intestines is challenging because of the effects from surrounding structures. However, calculating strain from images of intestinal fibrosis could be particularly useful to provide early detection of problematic areas that require surgical intervention.
At a much smaller scale, this DDE method is also applied to the cellular level by using higher resolution imaging techniques such as confocal microscopy. It serves, for example, in the characterization of extracellular matrix to understand how cells communicate under mechanical changes.
You’ve just watched JoVE’s introduction to quantitative strain visualization. You should now understand how to measure three-dimensional strain in biological tissues and how that is used in early disease detection. Thanks for watching!
