14.9:
ルシャトリエの原理:温度の変更
25,288 Views
•
•
質量作用の法則に従い、濃度の変化によって外乱を受けた平衡は、平衡定数Kの値が変化することなく、平衡を回復するために移動します。しかし、温度変化に応じて平衡が移動すると、異なる相対的な組成で平衡定数の値が変化するため、平衡が再構築されます。
この現象を理解するために、次の反応を考えます。
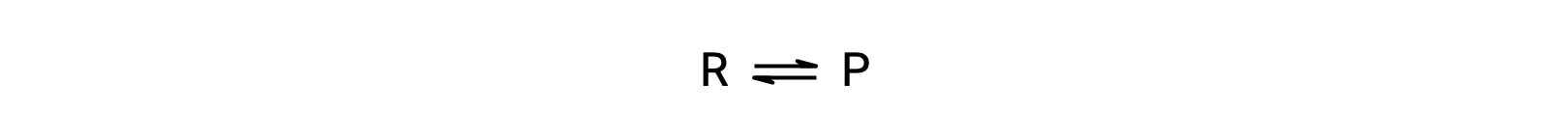
この反応は素過程にあたるので、平衡式の化学量論から直接、順方向と逆方向の速度則を導くことができます。’
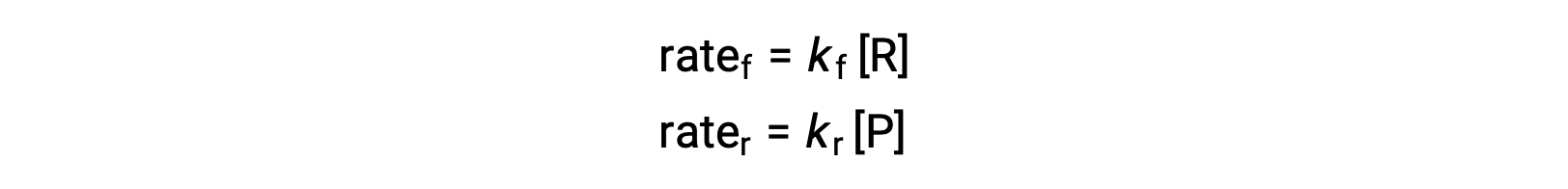
系が平衡にある時、次が成立します。
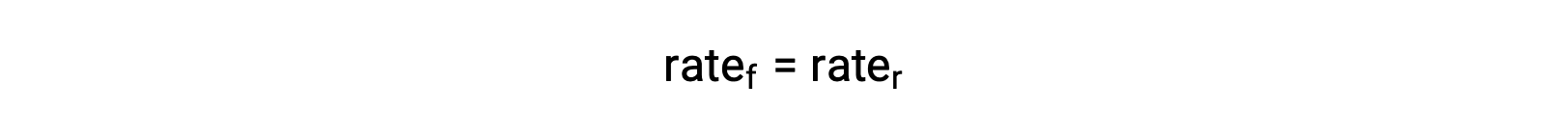
この等式に反応速度則を代入して再整理すると、
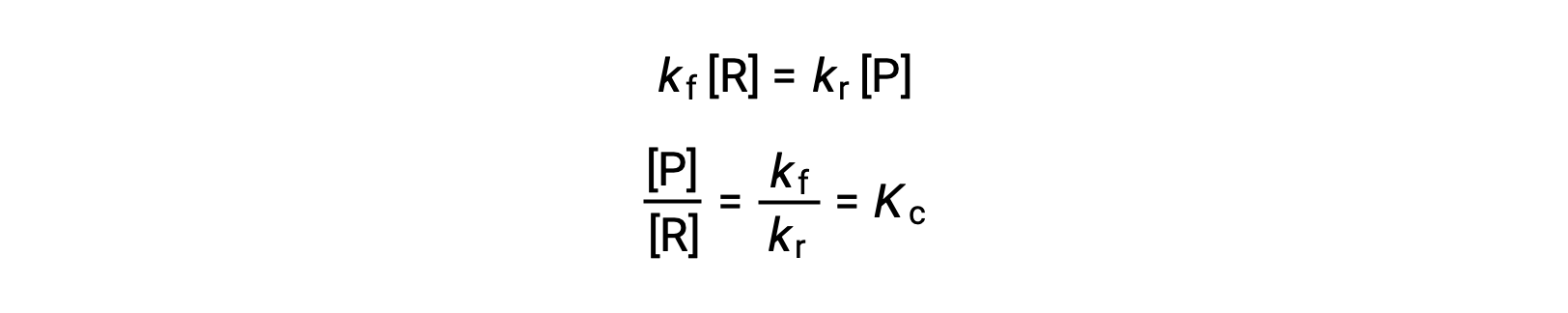
平衡定数は、順反応と逆反応の速度定数の数学的な関数として表すことができます。速度定数はアレニウスの式で表されるように温度によって変化するため、平衡定数も同様に温度によって変化する(速度定数が温度変化によって異なる影響を受けると仮定した場合)。多段階の反応機構を含むより複雑な反応の場合、平衡定数と機構内の各段階の速度定数の間には、同様の、より複雑な数学的関係が存在します。どんなに複雑な反応であっても、平衡定数の温度依存性は変わりません。
温度変化に対して平衡がどのように変化するかを予測するには、反応のエンタルピー変化を考慮するのが最も簡便です。例えば、ハーバー・ボッシュ法によるアンモニアの生成は、発熱を伴うプロセスです。
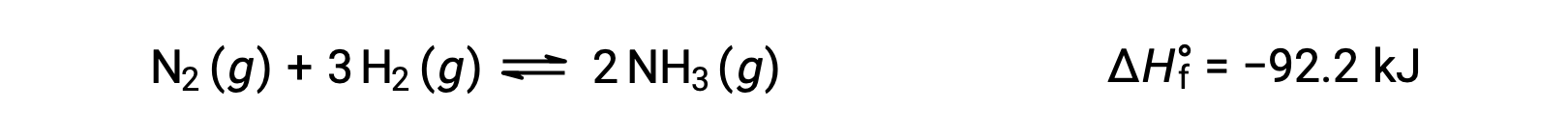
ルシャトリエの原理を適用するために、ここでの熱qは生成物と見なすことができます。
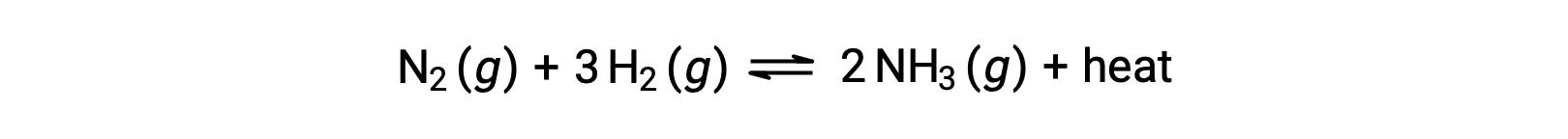
反応系の温度を上げることは、生成物の量を増やすことと同じなので、平衡は左にシフトします。系の温度を下げると、同様に平衡が右にシフトします。吸熱過程では、熱は反応の反応物とみなすことができ、逆の温度依存性が観察されます。
上記の文章は以下から引用しました。 Openstax, Chemistry 2e, Section 13.3 Shifting Equilibria: Le Châtelier’s Principle.
