Principe van Le Chatelier: Verandering in Temperatuur

Consistent with the law of mass action, an equilibrium stressed by a change in concentration will shift to re-establish equilibrium without any change in the value of the equilibrium constant, K. When an equilibrium shifts in response to a temperature change, however, it is re-established with a different relative composition that exhibits a different value for the equilibrium constant.

To understand this phenomenon, consider the elementary reaction:

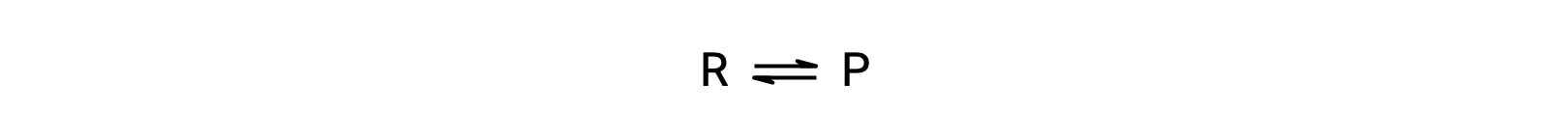
Since this is an elementary reaction, the rates laws for the forward and reverse may be derived directly from the balanced equation’s stoichiometry:

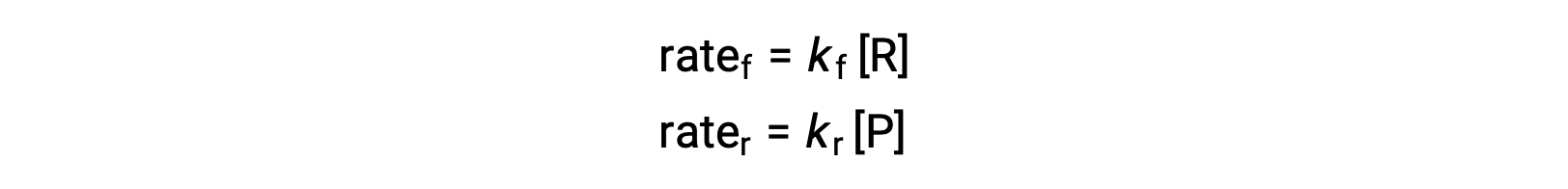
When the system is at equilibrium,

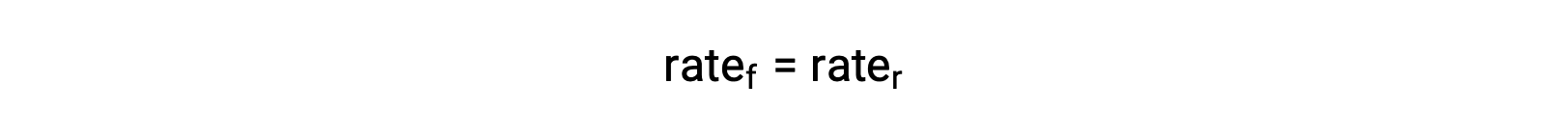
Substituting the rate laws into this equality and rearranging gives

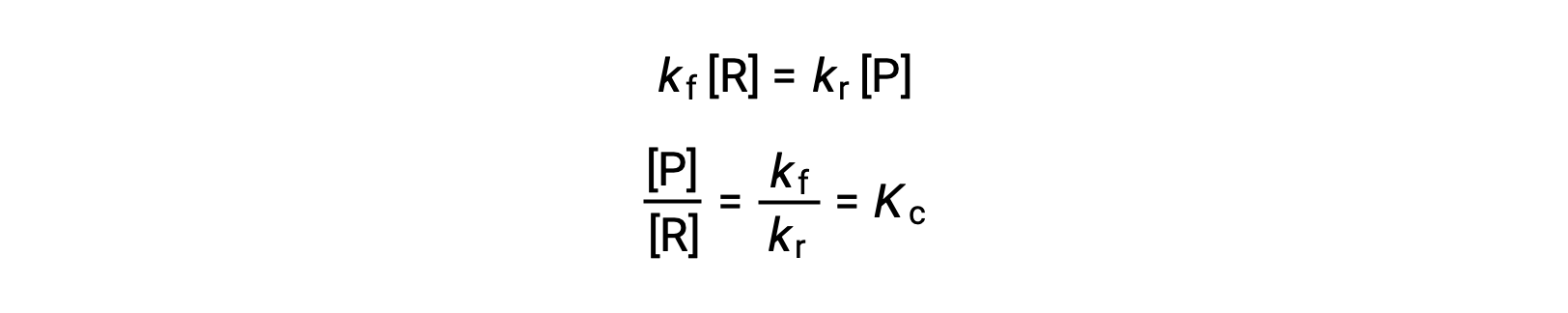
The equilibrium constant can be expressed as a mathematical function of the rate constants for the forward and reverse reactions. Since the rate constants vary with temperature as described by the Arrhenius equation, it stands to reason that the equilibrium constant will likewise vary with temperature (assuming the rate constants are affected to different extents by the temperature change). For more complex reactions involving multistep reaction mechanisms, a similar but more complex mathematical relation exists between the equilibrium constant and the rate constants of the steps in the mechanism. Regardless of how complex the reaction may be, the temperature-dependence of its equilibrium constant persists.

Predicting the shift an equilibrium will experience in response to a change in temperature is most conveniently accomplished by considering the enthalpy change of the reaction. For example, the formation of ammonia by the Haber’s process is an exothermic (heat-producing) process:

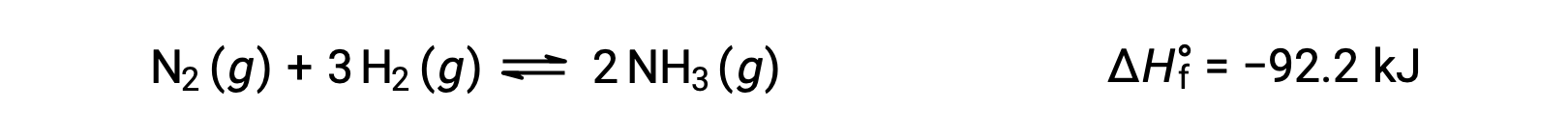
For purposes of applying Le Châtelier’s principle, heat, q, may be viewed as a product:

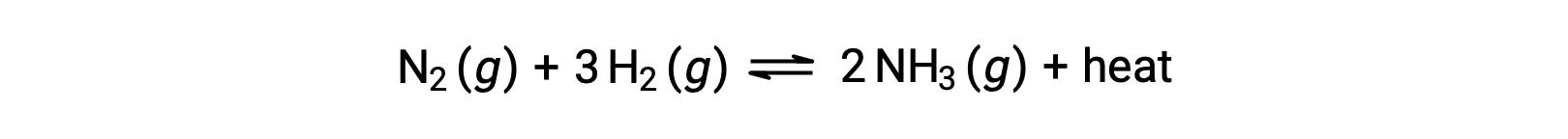
Raising the temperature of the system is akin to increasing the amount of a product, and so the equilibrium will shift to the left. Lowering the system temperature will likewise cause the equilibrium to shift right. For endothermic processes, heat is viewed as a reactant of the reaction and so the opposite temperature dependence is observed.

This text has been adapted from Openstax, Chemistry 2e, Section 13.3 Shifting Equilibria: Le Châtelier’s Principle.