13.8:
아레니우스 플롯
30,809 Views
•
•
Arrhenius 방정식은 화학 반응에 대한 활성화 에너지와 속도 상수, k와관련이 있습니다. Arrhenius 방정식에서, k = Ae−Ea/RT, R은 8.314 J /mol의 값을 가지고 이상적인 가스 상수입니다. K, T는 켈빈 스케일의 온도이고,Ea는 J/mole에서의 활성화 에너지이며, e는 상수 2.7183이며, A는 충돌 빈도 및 반응 분자의 방향과 관련된 주파수 인자라고 하는 상수이다.
Arrhenius 방정식은 실험 운동 데이터에서 반응의 활성화 에너지를 계산하는 데 사용할 수 있습니다. 반응을 위해 Ea를 결정하는 편리한 접근 방식은 두 개 이상의 다른 온도에서 k의 측정을 포함한다. 선형 방정식의 형태를 취하는 Arrhenius 방정식의 수정된 버전을 사용합니다.
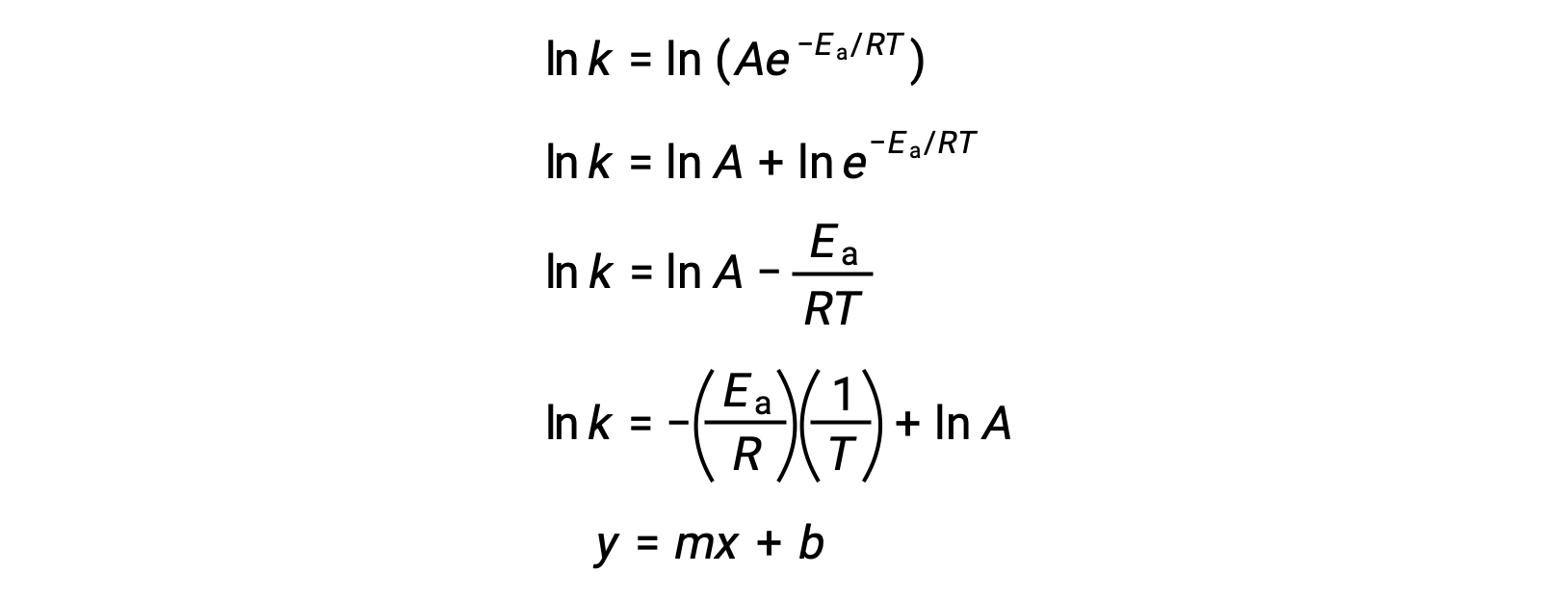
ln k 대 1/T의 플롯은 ln A와동일한 –EA/R 및 y-intercept와 동일한 경사로 선형입니다.
다음 반응을 고려하십시오.
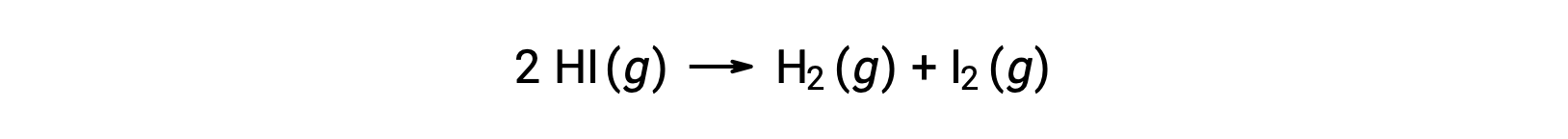
이 반응의 활성화 에너지는 온도와 일정한 속도의 변화가 반응 운동 데이터로부터 알려진지 확인할 수 있다.
| 온도(K) | 속도 상수(L/mol/s) |
| 555 | 3.52 ×10-7 |
| 575 | 1.22 × 10-6 |
| 645 | 8.59 × 10-5 |
| 700 | 1.16 × 10-3 |
| 781 | 3.95 × 10-2 |
제공된 데이터는 온도(1/T) 및 k(ln k)의자연 로그의 값을 도출하는 데 사용할 수 있다.
| 1/T (K-1) | ln k |
| 1.80 ×10-3 | –14.860 |
| 1.74 ×10-3 | –13.617 |
| 1.55 ×10-3 | –9.362 |
| 1.43 ×10-3 | –6.759 |
| 1.28 ×10-3 | –3.231 |

ln k 대1/T로파생된 데이터 점을 플로팅할 때 ln k와 1/T 사이의 선형 관계를 나타내는 라인 그래프가 생성되고, 도시된 바와 같이 생성된다.
활성화 에너지에 해당하는 선의 경사는 두 개의 실험 데이터 쌍을 사용하여 추정할 수 있습니다.

활성화 에너지를 유도하는 대안은 두 개의 서로 다른 온도에서 일정한 속도의 활용을 포함한다. 이 방법에서 Arrhenius 방정식은 편리한 2점 형태로 재배열됩니다.
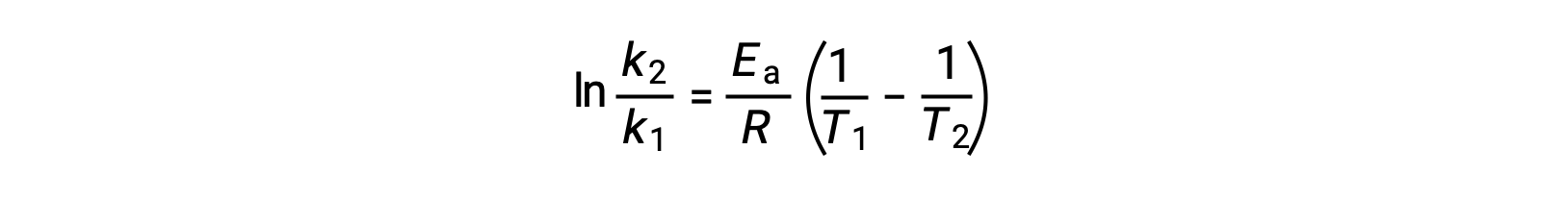
방정식을 재배치할 때 활성화 에너지에 대한 식이 생성됩니다.
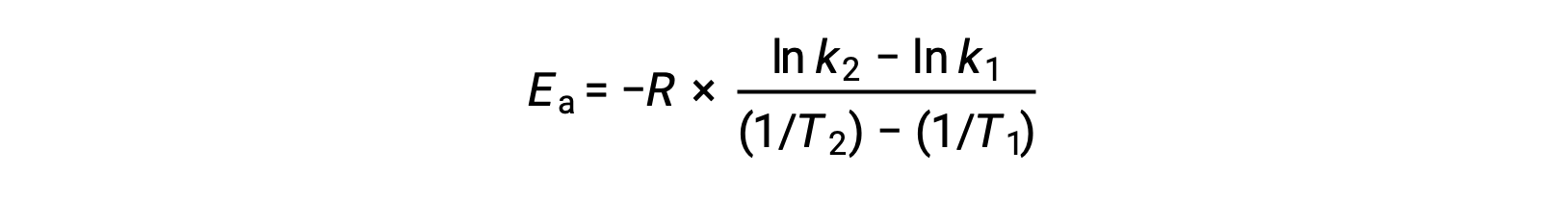
두 개의 데이터 쌍을 대체하고 추가 계산을 통해 두더지 또는 두더지 당 킬로줄당 줄의 활성화 에너지에 대한 가치를 산출합니다.
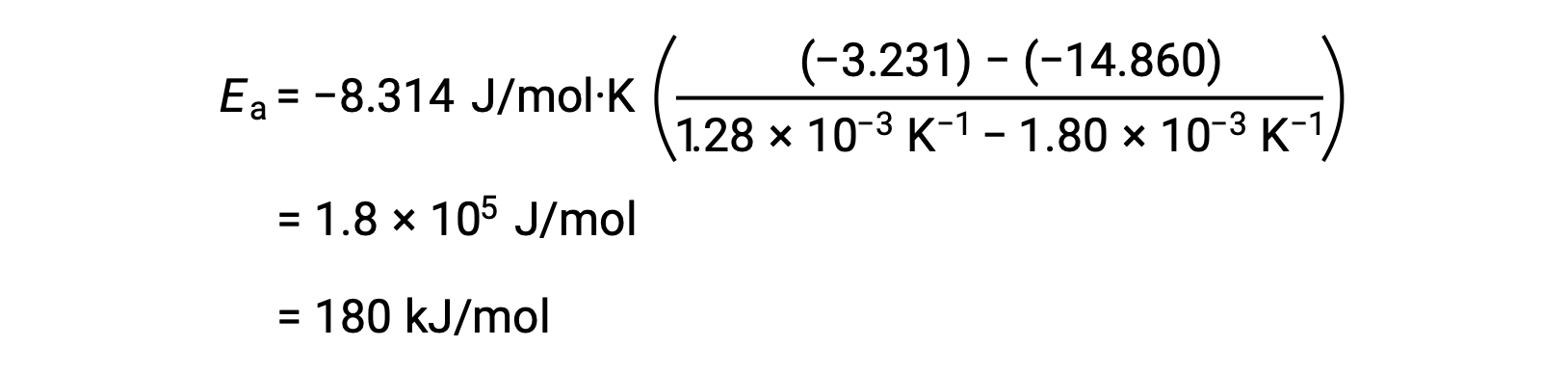
이 대체 2점 접근 방식은 그래픽 접근 방식과 동일한 결과를 얻을 수 있습니다. 그러나 실제로 그래픽 접근 방식은 일반적으로 실제 실험 데이터로 작업하는 동안 보다 신뢰할 수 있는 결과를 제공합니다.
이 텍스트는 Openstax, 화학 2e, 섹션 12.5: 충돌 이론에서적용됩니다.
