Orientational Transition in a Liquid Crystal Triggered by the Thermodynamic Growth of Interfacial Wetting Sheets

Satoshi Aya; Fumito Araoka

doi:10.3791/55729

JoVE Journal > Engineering

Engenharia

Orientational Transition in a Liquid Crystal Triggered by the Thermodynamic Growth of Interfacial Wetting Sheets

Published: May 15, 2017

doi:

10.3791/55729

Satoshi Aya¹, Fumito Araoka¹

¹RIKEN Center for Emergent Matter Science (CEMS)

Summary

Here, we present a protocol to trigger an orientational transition of a liquid crystal in response to temperature. Methodologies are described for preparing a sample in order to observe the transition and the detailed transitional evolution.

Abstract

In liquid crystal (LC) physical chemistry, molecules near the surface play a great role in controlling bulk orientation. Thus far, mainly to achieve desired molecular orientation states in LC displays, the “static” surface property of LCs, so-called surface anchoring, has been intensively studied. As a rule of thumb, once the initial orientation of LCs is “locked” by specific surface treatments, such as rubbing or treatment with a specific alignment layer, it hardly changes with temperature. Here, we present a system exhibiting an orientational transition upon temperature variation, which conflicts with the consensus. Right on the transition, the bulk LC molecules experience the orientational rotation, with 90° between the planar (P) orientation at high temperatures and the vertical (V) orientation at low temperatures in the first-order transitional manner. We have tracked thermodynamic surface anchoring behavior by means of polarizing optical microscopy (POM), dielectric spectroscopy (DS), high-resolution differential scanning calorimetry (HR-DSC), and grazing incidence X-ray diffraction (GI-XRD) and reached a plausible physical explanation: that the transition is triggered by a growth of surface wetting sheets, which impose the V orientation locally against the P orientation in the bulk. This landscape would provide a general link explaining how the equilibrium bulk orientation is affected by surface-localized orientation in many LC systems. In our characterization, POM and DS are advantageous by offering information on the spatial distribution of the orientation of LC molecules. HR-DSC gives information about the precise thermodynamic information on transitions, which cannot be addressed by conventional DSC instruments due to limited resolution. GI-XRD provides information on surface-specific molecular orientation and short-range orderings. The goal of this paper is to present a protocol for preparing a sample that exhibits the transition and to demonstrate how the thermodynamic structural variation, both in the bulk and on surfaces, can be analyzed through the abovementioned methods.

Introduction

In recent years, there has been growing interest in learning how dynamic molecular features and structures of surface molecules in response to external stimuli might affect the bulk orientation of materials in LC states. One example is to use LC biosensors as a new application of LCs¹^,². To quantify how many target bio-species are detected, it is important to know how the interfacial LCs that contact adhering target molecules change and evolve, while also detecting and how they transfer/translate their properties into the bulk.

Using models to pursue these answers, we started with systems that have their surface molecular orientation and short-range orderings varying thermodynamically. These systems allow us to correlate the changes in surface orientation and orderings with the resulting bulk orientation in a systematic way. Recently, we found several LC systems that exhibit orientational transitions, where a spontaneous bulk molecular orientation changes with temperature. In principle, orientational transitions can be categorized into either quasi-second-order³^,⁴ or quasi-first-order transition⁵^,⁶^,⁷^,⁸. The former is accompanied by a continuous bulk molecular reorientation upon changes in temperature, whereas the latter demonstrates a discontinuous one. In this article, we describe an orientational transition in the quasi-first-order manner between the P and the V orientational states. It proceeds in the single nematic (N) phase by changing the temperature. Details will be provided in the Representative Results and the Discussion.

Since orientational change in the bulk should be governed by a change in the surface molecular orientation and short-range orderings, it is apparent that this system can potentially offer insights into how the thermodynamic variation in surface molecular orientation and short-range orderings affects the bulk orientation. In this article, with the goal of understanding the abovementioned issues, we tackled three problems using four complementary methods (i.e., POM, DS, HR-DSC, and GI-XRD): (1) What does the orientational transition look like? (2) Is the orientational transition thermally detectable? (3) Why and how does the orientational transition occur?

Protocol

1. Preparation of the Liquid Crystal Alignment Layer of a Perfluoropolymer onto Glass Substrates

Preparation of the perfluoropolymer solution
1. Prepare 1 mL of the perfluoropolymer solution by dissolving a perfluoropolymer solution (9 wt% polymer) in a commercial solvent at a ratio of 1:2; this ensures uniform films 0.5-1 µm thick to be spin-coated.
  NOTE: Please see the Materials List for the solution and solvent used.
Coating of the perfluoropolymer onto clean glass substrates
1. Wash the glass substrates (typical size: 1 cm x 1 cm) by sonication at 38 or 42 kHz in an alkaline detergent. Repeatedly rinse them with distilled water. Typically, rinse more than 10 times, with 5 min of sonication each time.
2. Subject the substrates to UV-O₃ cleaner for 10 min.
3. Drip 20 µL of the solution from step 1.1 onto the cleaned glass substrates. Immediately spin-coat the solution at 3,500 rpm and room temperature for 70 s. Bake the film at 80 °C for 60 min to remove the solvent and at 200 °C for 60 min for curing.

2. Preparation of LC Cells

Glue two glass substrates coated with film together using a photo-curable resin and an LED lamp with a wavelength of 365 nm (1.1 W/cm²). Adjust the thickness of the gap between the two substrates to within the range of 2-100 µm by using micrometer-size glass particles or polyethylene naphthalate films.
Introduce an LC material, 4'-butyl-4-heptyl-bicyclohexyl-4-carbonitrile (CCN47; 0.2-10 µL)⁹ to the prepared LC cells using a spatula under capillary force at a temperature higher than the isotropic liquid (I)-nematic (N) phase transition temperature.
NOTE: CCN47 has a negative dielectric anisotropy, and the phase sequence is Cry 298.6 K SmA 301.3 K N 331.3 K I, where Cry and SmA stand for crystal and smectic A phases. Do not introduce CCN47 in the N phase or SmA phase, because flow-induced alignment would be promoted.

3. Sample Characterization

Texture observation by polarizing optical microscopy (POM)¹⁰
1. Observe the LC cells under POM with 4-100X objective lenses in conjunction with a hot stage to control the sample temperature with ± 0.1-K accuracy. Record the textures in more than 5 frames, at even intervals per Kelvin. Use a digital color camera sequentially, both upon cooling and heating in the range of 291-343 K.
Dielectric spectroscopy (DS)¹¹
1. Prepare LC cells, with ITO electrodes – which can have a square or circular shape and can be purchased commercially – on both substrates. Solder a lead wire to each substrate.
  NOTE: Please see the Materials List for the substrates used.
2. Measure the capacitance or dielectric constant of the LC cells, exactly as used for POM, using a commercial impedance/gain-phase analyzer. Ensure that the state of the samples is equilibrated before each measurement. Measure the time-dependence of capacitance or the dielectric constant of the LC cells by measuring the capacitance of the LC cells manually every 5 min.
3. Start the DS measurement only if the capacitance or dielectric constant of the LC cells becomes non-time-dependent.
High-resolution differential scanning calorimetry (HR-DSC)¹²
1. Put the LC cells into a home-made HR-DSC to be examined, exactly as in POM (never use DSC pans). Refer to Reference 12 to design and build an HR-DSC and to learn how to use it. Perform measurements with scan rates of 0.05-0.10 K/min to enhance the minimum temperature resolving power.
Grazing incident X-ray diffraction (GI-XRD)¹³
1. Put either the LC cell (used for POM or DSC) or a sample with a 2 to 5 µL droplet of CCN47 onto a coated substrate on the GI-XRD sample stage, which should be equipped with a temperature controller.
2. Equilibrate the sample for more than 10 min at desired temperatures in the range of 291-343 K, both upon cooling and heating.
3. Use an incident X-ray beam on the sample, with a minute incident angle around 0.05-0.10°, to extract surface information on molecular orientation and orderings/structures. Swing the incident angle of the X-ray beam to find the optimal incident angle at which the strength of the diffraction is the strongest. Take the measurements at the optimal incident angle.
  NOTE: Keep in mind that GI-XRD makes it possible to probe interfacial peculiarities on the nanometer scale, thus maximizing the signal from thin layers while minimizing the signal from the bulk. Note that normal XRD geometries, other than GI-XRD, are not surface-sensitive methods, since the X-ray radiation beam has a large penetration depth into materials.

Representative Results

POM images, DS data, HR-DSC data, and GI-XRD patterns were collected during temperature variation, especially in the vicinity of the orientational transition upon both cooling and heating.

Figure 1 represents the evolution of the texture made by POM and DS measurements during the POM observation of the orientational transition from the P (V) to the V (P) orientational state during cooling (heating). The reorientation process during the orientational transition based on the POM observation (Figure 1a) is shown. Upon cooling, the P orientation in the bulk is right below the I-N transition temperature, made distinct by the appearance of two- (in the majority) and four-brush Schlieren textures. It is worth noting that the two-brush Schlieren (disclination with a topological strength of s = ±1/2) is one of resultant structures with a line defect, which topologically does not allow pretilt in the surface director¹⁴. On the other hand, the four-brush Schlieren (disclination with a topological strength of s = ±1) has a point singularity, which can exist either on surfaces or in the bulk. Unlike two-brush Schlieren, a pretilt of the surface director is allowed according to symmetry arguments. By lowering the temperature down to 321.5 K, dark domains (the V orientation) nucleate primarily from the point singularities of the ±1 disclination and spread with time. By annealing the sample for several minutes or by allowing for further cooling, the whole field of vision becomes completely dark, suggesting the completion of the transition from the P to the V orientation in the bulk. Upon heating, the reversal orientational transition from the V to the P orientation in the bulk happens with an important dissimilarity to that of cooling: a hysteresis around 5 K, suggesting a strong first-order transition, was found. Note that the typical hysteresis ranges of LC-LC transitions (e.g., the I-N and the N-Smectic phase transitions) are less than 1 K.

Figure 2 shows HR-DSC data representing the heat flow through the sample as a function of the temperature (Figure 2a) and time (the inset of Figure 2b) measured by HR-DSC. The data in the inset of Figure 2b was used to analyze the Avrami exponent after the orientational transition (Figure 2b).

Figure 3 shows GI-XRD patterns in two sample geometries at various temperatures: droplet geometry (Figure 3a, top) and in situ LC cell geometry (Figure 3a, bottom). Both demonstrate short-range ordering of quasi-SmA wetting sheets, with layer structures (hereafter abbreviated as SSWS) formed in the vicinity of the surface. The size of the SSWS was calculated from full width at half maximum (FWHM) of the GI-XRD peaks (Figure 3b). There are two crucial observations affirming that the SSWS should be the surface-specific structure: (1) SmA ordering is absent in the bulk of CCN47, as confirmed by XRD (not shown here). (2) Isotropic diffraction patterns, both at SAD (weaker and broader than those in the perfluoropolymer surface) and at WAD, were confirmed on a conventional P alignment layer material, confirming the special molecular interactions between the perfluoropolymer and CCN47. Since the arguments on the molecular interactions go beyond the scope of the present discussion, they will be reported elsewhere in the future. Surprisingly, even in the temperature range of the P orientational state (see GI-XRD patterns at 328 and 322 K), SSWS persists, indicating that the surface orientational condition is frustrated. Some parts of the surface are under the cloak of SSWS, exhibiting the V alignment capability for the bulk LC molecules, whereas the rest are exposed to exhibit the P alignment capability. If the size or coverage of SSWS changes with temperature, we expect that the bulk LC orientational state might be varied, since the ratio of the V alignment capability to the P alignment capability changes accordingly. To confirm this possibility, the temperature-dependence of the SSWS correlation length (i.e., the average persistent length of the SmA short-range order in the direction normal to the surface) was calculated from the FWHM of the SAD peaks. Figure 3b confirms the expected trend showing an increase in the SSWS correlation length over the N phase, as well as an underlying hysteresis. The hysteresis means that once the SSWS is formed on the surface upon cooling, it is thermodynamically stable and is durable, even at high temperatures. The key feature is that the hysteresis range is consistent with the hysteresis range confirmed by POM and DS (Figure 1). This suggests that the orientational transition is triggered by the growth of SSWS.

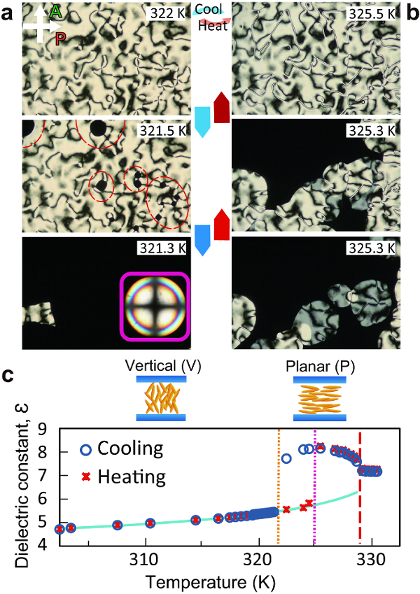
Figure 1: Evolution of the orientational transition from the P to V orientational state, both on cooling and on heating. Texture variation on (a) cooling (blue downward arrows) and (b) heating (red upward arrows). (a) Top: The P orientation appears just below the I-N transition. (a) Middle: At T_C(i.e., orientational transition temperature upon cooling), the V orientation emerges from the point defect of the predominately four-brush Schlieren texture (red dashed circles). (a) Bottom: The domains with the V orientation expand and cover the whole field of view, as supplemented by an inset of a conoscopic image. Note that the cruciform conoscopic image shows little change at low temperatures. (b) Bottom: At T_H(i.e., orientational transition temperature upon heating), the dark and bright Schlieren textures make their appearance from the V orientational domain, suggesting the coexistence of thin and thick layers with the P orientation. (b) Middle: Dark domains transform to bright domains. (b) Top: The director over the entire field of view field is the P orientation, exhibiting a thin four-brush Schlieren texture. (c) The temperature-dependence of the dielectric constant measured upon both cooling (open circles) and heating (cross marks). The blue line is the experimental data of the dielectric constant of CCN47, measured in a homeotropic LC cell. This figure has been modified and adapted with permission from Reference 15. Copyright 2012, The American Physical Society. Please click here to view a larger version of this figure.

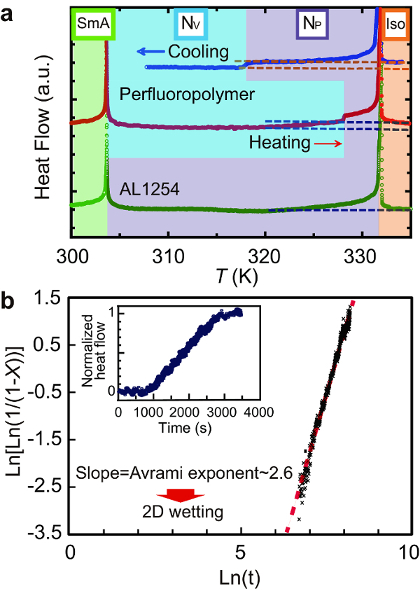
Figure 2: Thermal trace of the orientational transition using the HR-DSC. (a) HR-DSC charts in a cell coated with the perfluoropolymer after both cooling and heating. The result in an LC cell coated with a conventional planar alignment layer material, AL1254, after cooling is also shown as a control measurement. The baselines of three HR-DSC charts are properly shifted. A double-arrowed scale bar corresponds to 1 mW/g. Dashed lines are drawn to emphasize that the heat flow in the V orientation is smaller than those in both the P orientation and in the I phase in the cell with the perfluoropolymer surface. (b) Avrami fitting for the nucleation-growth process of domains, with the V orientation accruing from domains with the P orientation after cooling. The variation of the heat flow with time is shown in the inset, which was used for the Avrami fitting. This figure has been modified and adapted with permission from references^7,8. Copyright 2012, The American Physical Society, Copyright 2016, American Chemical Society. Please click here to view a larger version of this figure.

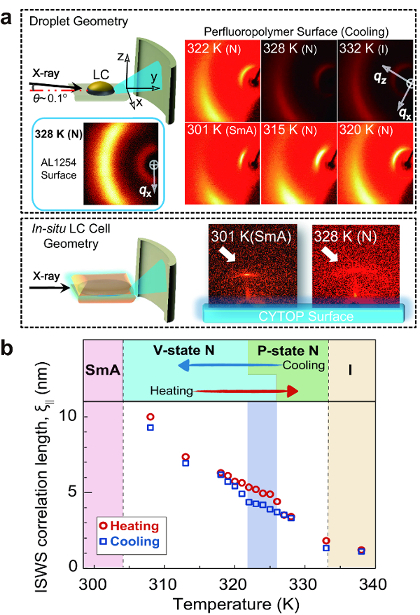
Figure 3: Analysis of the thermodynamic variation of the interfacial LC structure. (a) The variation in the GI-XRD pattern with respect to temperature using a CCN47 droplet on the perfluoropolymer surface and an LC cell on the perfluoropolymer surface. The GI-XRD pattern of the CCN47 droplet on a surface with the P alignment layer material AL1254 is shown as a reference. (b) Temperature-dependence of the smectic correlation length, ξ_∥, upon both cooling and heating, calculated from the full width at half-maximum of the small-angle diffraction pattern of GI-XRD. This figure has been modified and adapted with permission from references⁷^,⁸. Copyright 2012, The American Physical Society; Copyright 2016, American Chemical Society. Please click here to view a larger version of this figure.

Discussion

The 10x POM images taken using a 5-µm LC cell (Figures 1a and b) clearly show that the orientational state of the bulk LC molecules transits between the P and the V orientations upon temperature variation in a first-order manner. This is marked by the domain nucleation and growth processes, with a new orientation differing from the initial orientation by 90°. The transition temperatures upon cooling and heating are 321.5 K and 325.3 K, respectively. Since CCN47 has a birefringence of ~0.02⁹, the visibility of the Schlieren texture is good when the thickness of the LC cells is in the range of 5-20 µm. If the thickness is smaller than this range, the transmittance of the Schlieren texture becomes lower, which results in worse visibility. On the other hand, if the thickness is larger than this range, interference and scattering of light results in aberrations in the POM images, lowering the visibility and even the effective optical resolution.

To quantitatively investigate the tilt angle of the LC director with respect to the normal surface (i.e., the polar angle) in the bulk, DS measurement at a fixed frequency of 1 kHz (far away from the conductive frequency range) were carried out concomitantly with POM as a function of temperature (Figure 1c). Since the dielectric anisotropy of the LC used are measured in advance as a function of temperature by using cells with both P and V alignment layers, the change in the dielectric permittivity (ℇ) upon the orientational transition can be translated to the change in the polar angle of the LCs in the bulk. In Figure 1c, the trace of ℇ upon both cooling and heating explicitly show that the orientational transition from the P (V) to the V (P) occurs abruptly, with large a jump in the trace. It is evident from the large discontinuity in ℇ that the orientational transition has a first-order nature, consistent with the observation made by POM. Even though DS measurement is powerful enough to estimate the polar angle of anisotropic materials on average, it lacks the depth resolution and cannot give any information on the in-plane azimuthal orientation.

In Figure 2a, the HR-DSC trace in a 25 µm LC cell confirms a stepwise change in the heat flow, crossing at the orientational transition upon cooling at ~318 K (heating at ~328 K), at which point the bulk orientational state changes from the P to the V state. Also, the heat anomalies at the bulk I-N phase transition at ~332 K and at the bulk N-SmA phase transition at ~303 K. A scan rate higher than 0.05-0.10 K/min would result in worse temperature-resolving power and noise in the heat flow and would bring the target sample out of equilibrium. The quasi-stepwise change in the heat flow upon the orientational transition does not accompany measurable latent heat, which represents the potential energy stored in the bonds between the molecules. This is different from the normal LC and crystalline phase transitions involving a substantial latent heat. This means that the heat flow rate per unit volume, dQ/dtdV, is directly associated with the specific heat capacity C_p (i.e., dQ/dtdV∼C_p). This consequence makes it possible to determine the fraction of the bulk molecules (X) that has completed the orientational transition from P to the V. In turn, this offers an understanding of the nucleation and growth processes of the orientational transition through Kolmogorov-Johnson-Mehl-Avrami, (KJMA or Avrami) analysis¹⁶^,¹⁷^,¹⁸. Figure 2b presents the Avrami fitting based on the equation 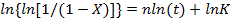, where X, K, t, and n are the volume fraction of the new domains, the temperature-dependent Avrami coefficient, time, and the Avrami exponent, respectively). n was confirmed to be ~2.6, suggesting a heterogeneous nucleation and subsequent 2D growth interfacial wetting processes. This result comes in sharp contrast to the Avrami exponent for the isotropic-nematic transition (n ≈ 3.6) in usual bulk NLCs (please refer to the Supporting Information in Reference 8). Note that the present KJMA analysis is possible thanks to both the excellent temperature-resolving power and the good signal-to-noise ratio in our HR-DSC. This cannot be achieved by conventional DSC instruments. Since this technique is sensitive to small variations in the heat flow (e.g., even the nucleation/growth processes of nanofilaments are detectable¹⁹), it has the potential to measure small changes in the structures and phases of any material, ranging from (in)organic materials to metals. In addition, we emphasize that this technique has fewer limitations in sample geometry (e.g., the LC cells that cannot be measured by conventional DSC instruments).

The GI-XRD patterns for the samples with a perfluoropolymer surface (Figure 3a) confirm both the SAD and WAD peaks, with directivity at temperatures other than 332 K of the I phase. The former, which represents the orderings along the long axes of LC molecules, runs parallel to the surface. The latter, which represents the orderings along the short axes of LC molecules, is located in positions perpendicular to the former. The intensity of SAD peaks is stronger than that of WAD peaks, and the FWHM of SAD peaks is also narrower than that of WAD peaks. Since the FWHM of diffraction peaks is the principle measure of the degree of the strength of positional correlation between molecules, it turns out that stronger positional correlation along the long axes of LC molecules, rather than along the short ones, is present. This demonstrates the existence of the abovementioned SSWS in the vicinity of the surface. As seen from Figure 3b, the smectic correlation length of several molecular lengths is in the nanometer scale. Such information, in the nanoscopic to mesoscopic scale, localized in the interfacial region can only be extracted by surface-sensitive XRD geometry, such as in GI-XRD, but not by conventional transmission and reflection geometries. Also, if the incident angle of GI-XRD is too large (~ >0.1°), the total reflection condition will be broken and the surface-specific structures can no longer be probed.

Declarações

The authors have nothing to disclose.

Acknowledgements

This work was supported by JSPS KAKENHI grant Number 16H06037. We sincerely thank Dr. Yuji Sasaki in Hokkaido University for technical assistance for HR-DSC.

Materials

CYTOP	Asahi Glass Co. Ltd.	CTX-809A
Solvent for CYTOP	Asahi Glass Co. Ltd.	CT-180 Sol.
Alkaline detergent	Merck KGaA	Extran MA01
NOA61	Norland Products, Inc.	#37-322	Purchasable from Edmund Optics
AL1254	JSR Corporation		Planar alignment material in self-made cells
4’-butyl-4-heptyl-bicyclohexyl-4-carbonitrile	Nematel GmbH & Co. KG		Custom-made
UV-O3 cleaner	Technovision Inc.	UV-208
Hot-stage system	Mettler Toledo	HS82
High-Definition Color Camera Head	Nikon	DS-Fi1
Impedance/gain-phase analyzer	Solartron Analytical	1260
Indium Tin Oxide (ITO)-coated substrate	GEOMATEC Co. Ltd.		Custom-made

Referências

Woltman, S. J., Jay, G. D., Crawford, G. P. Liquid-Crystal Materials Find a New Order in Biomedical Applications. Nat. Mater. 6 (12), 929-938 (2007).
Carlton, R. J., et al. Chemical and Biological Sensing Using Liquid Crystals. Liq. Cryst.Rev. 1 (1), 29-51 (2013).
Patel, J. S., Yokoyama, H. Continuous Anchoring Transition in Liquid Crystals. Nature. 362, 525-527 (1993).
Senyuk, B., et al. Surface alignment, anchoring transitions, optical properties, and topological defects in the nematic phase of thermotropic bent-core liquid crystal A131. Phys Rev E. 82 (4 Pt 1), 041711 (2010).
Bechhoefer, J., et al. Critical Behavior in Anchoring Transitions of Nematic Liquid Crystals. Phys. Rev. Lett. 64 (16), 1911-1914 (1990).
Dhara, S., et al. Anchoring Transitions of Transversely Polar Liquid-Crystal Molecules on Perfluoropolymer Surfaces. Phys. Rev. E. 79 (6 Pt 1), 60701 (2009).
Aya, S., et al. Stepwise heat-capacity change at an orientation transition in liquid crystals. Phys. Rev. E. 86 (2), 022512 (2014).
Aya, S., et al. Thermodynamically Anchoring-Frustrated Surface to Trigger Bulk Discontinuous Orientational Transition. Langmuir. 32 (41), 10545-10550 (2016).
Dhara, S., Madhusudana, N. V. Physical characterisation of 4′-butyl-4-heptyl-bicyclohexyl-4-carbonitrile. Phase Trans. 81 (6), 561-569 (2008).
Dierking, I. . Textures of Liquid Crystals. , (2003).
Perkowski, P., et al. Technical aspects of dielectric spectroscopy measurements of liquid crystals. Opto-Electronics Review. 16 (3), 271-276 (2008).
Inaba, H. Nano-watt stabilized DSC and ITS applications. J Therm Anal Calorim. 79 (3), 605-613 (2005).
Leveiller, F., Boehm, C., Jacquemain, D. Two-dimensional crystal structure of cadmium arachidate studied by synchrotron X-ray diffraction and reflectivity. Langmuir. 10 (3), 819-829 (1994).
de Gennes, P. G., Prost, J. . The Physics of Liquid Crystals (Second Edition). , (1993).
Aya, S., et al. Critical Behavior in an Electric-Field-Induced Anchoring Transition in a Liquid Crystal. Phys. Rev. E. 86 (1 Pt 1), 10701 (2012).
Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 7, 1103-1112 (1939).
Avrami, M. Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei. J. Chem. Phys. 8 (2), 212-224 (1939).
Avrami, M. Granulation Phase Change, and Microstructure Kinetics of Phase Change. III. J. Chem. Phys. 9, 177-184 (1941).
Sasaki, Y., et al. Distinctive Thermal Behavior and Nanoscale Phase Separation in the Heterogeneous Liquid- Crystal B4 Matrix of Bent-Core Molecules. Phys. Rev. Lett. 107 (23), 237802 (2011).

Play Video

PDF

DOI

DOWNLOAD MATERIALS LIST

Citar este artigo

Aya, S., Araoka, F. Orientational Transition in a Liquid Crystal Triggered by the Thermodynamic Growth of Interfacial Wetting Sheets. J. Vis. Exp. (123), e55729, doi:10.3791/55729 (2017).