Énergie de liaison nucléaire

La différence entre les masses calculées et celles mesurées expérimentalement est connue sous le nom du défaut de masse de l’atome. Dans le cas de l’hélium 4, le défaut de masse indique une “perte” de masse de 4,0331 uma – 4,0026 uma = 0,0305 uma. La perte de masse qui accompagne la formation d’un atome à partir de protons, de neutrons et d’électrons est due à la conversion de cette masse en énergie qui s’est développée à mesure que l’atome se formait. L’énergie de liaison nucléaire est l’énergie produite lorsque les nucléons des atomes sont liés ensemble ; c’est aussi l’énergie nécessaire pour briser un noyau en ses protons et neutrons constitutifs. Les changements d’énergie associés aux réactions nucléaires sont beaucoup plus importants que ceux des réactions chimiques.

La conversion entre la masse et l’énergie est représentée de façon plus identifiable grâce à l’équation de l’équivalence masse–énergie telle qu’indiquée par Albert Einstein : E = mc², où E est l’énergie, m est la masse de matière qui est convertie et c est la vitesse de la lumière dans le vide. À l’aide de cette équation d’équivalence masse–énergie, l’énergie de liaison nucléaire d’un noyau peut être calculée à partir de son défaut de masse. Une grande variété d’unités sont couramment utilisées pour les énergies de liaison nucléaires, y compris les électronvolts (eV), avec 1 eV équivalant à la quantité d’énergie nécessaire pour déplacer la charge d’un électron à travers une différence de potentiel électrique de 1 volt : 1,602 × 10^–19 J.

Pour calculer l’énergie de liaison à partir du défaut de masse, on exprime d’abord le défaut de masse en g/mol. Ceci est facile à faire compte tenu de l’équivalence numérique de la masse atomique (uma) et de la masse molaire (g/mol) qui résulte des définitions des unités uma et mole. Le défaut de masse du He 4 est donc de 0,0305 g/mol. Pour tenir compte des unités des autres termes de l’équation masse–énergie, la masse doit être exprimée en kilogrammes, puisque 1 J = 1 kg m²/s². La conversion des grammes en kilogrammes donne un défaut de masse de 3,05 × 10^–5 kg/mol. Lorsque cette quantité est remplacée dans l’équation d’équivalence masse–énergie, cela donne :

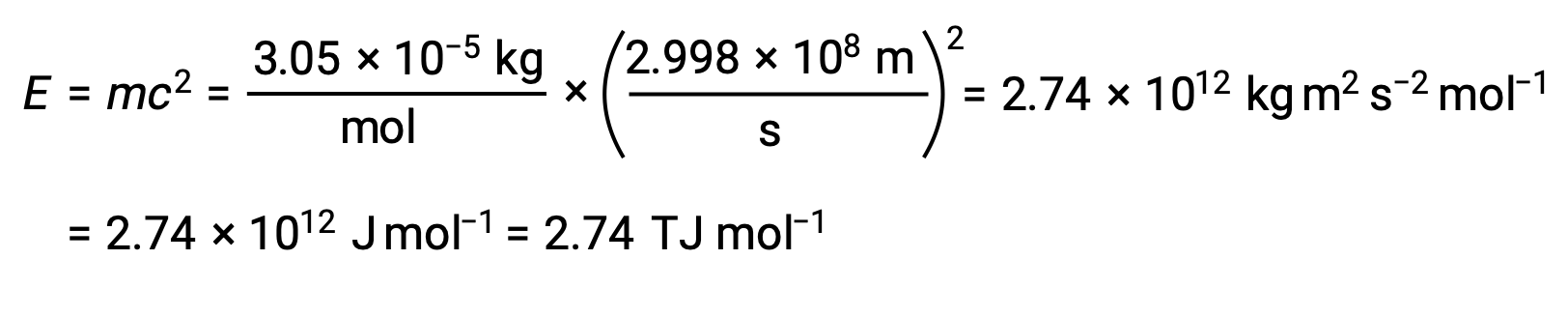
L’énergie de liaison pour un seul noyau est calculée à partir de l’énergie molaire de liaison en utilisant le nombre d’Avogadro :

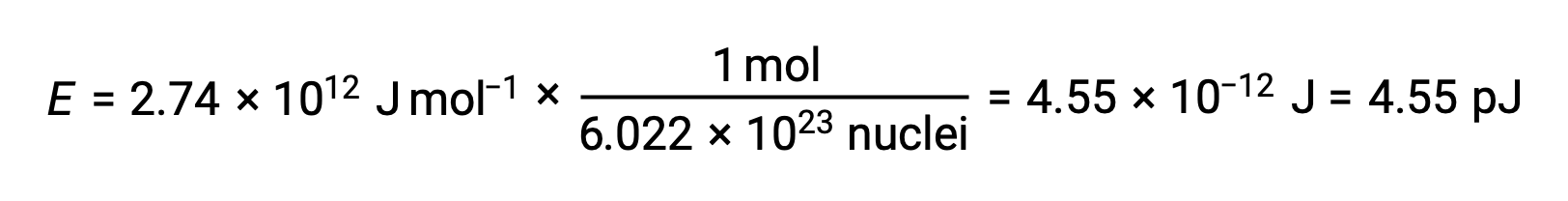
On rappelle que 1 eV = 1,602 × 10^–19 J. En utilisant l’énergie de liaison calculée :

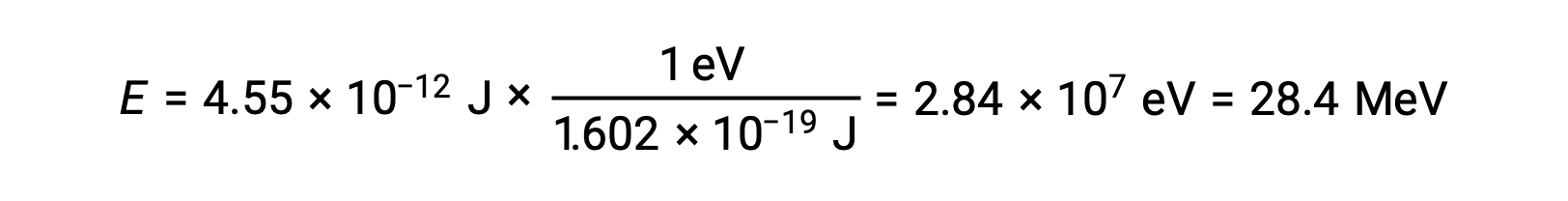
La stabilité relative d’un noyau est corrélée à son énergie de liaison par nucléon, l’énergie de liaison totale du noyau divisée par le nombre de nucléons dans le noyau. Par exemple, l’énergie de liaison d’un noyau d’hélium 4 est de 28,4 MeV. L’énergie de liaison par nucléon d’un noyau d’hélium 4 est donc :

L’énergie de liaison par nucléon est la plus importante pour les nucléides dont le nombre de masse est d’environ 56.

Ce texte est adapté de Openstax, Chimie 2e, Section 21.1 : Structure et stabilité nucléaires.