17.2:
エントロピー
24,121 Views
•
•
水に溶解した塩の粒子は、溶液中で自発的に集まって固体粒子を形成することはありません。また、真空中で膨張した気体は分散したままで、自然に再集合することはありません。これらの現象が一方向であるのは、エントロピー(S)と呼ばれる熱力学的な状態関数の結果です。エントロピーとは、エネルギーが系全体にどの程度分散しているかを示す尺度であり、言い換えれば、熱力学的な系の無秩序の度合いに比例するものです。エントロピーは、系に物理的または化学的な変化が生じると、増加( ΔS > 0、無秩序化)または減少( ΔS < 0、秩序化)します。エントロピーの変化は、最終状態と初期状態のエントロピーの差であり、 ΔS = Sf – Si となります。
ボルツマンの微視的状態理論
微視的状態とは、系を構成する原子や分子のすべての位置とエネルギーが特定された配置のことです。系のエントロピーと可能な微視的状態の数(W)の関係は、S = k ln Wであり。ここでkはボルツマン定数で、1.38 × 10−23 J/Kです。
エントロピーの変化は、次のように表されます。
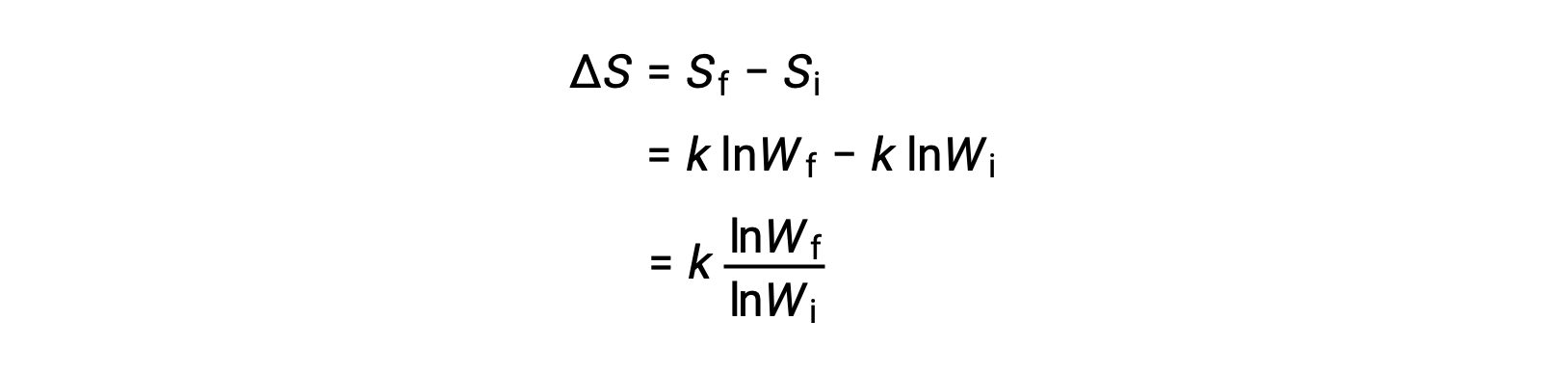
可能な微視的状態の数が多い系は、微視的状態の数が少ない秩序系(エントロピーが低い)よりも無秩序(エントロピーが高い)です。微視的状態の数の増加を伴う過程では系のエントロピーが増加し(Wf > Wi)、 ΔS> 0となります。逆に微視的状態の数を減らすプロセスでは、系のエントロピーは減少し(Wf < Wi)、 ΔS < 0となります。
接続された2つのフラスコの間に理想気体が分布することを考えます。最初は、気体の分子は2つのフラスコのうちの1方のみに閉じ込められています。フラスコの間のバルブを開くと、気体分子が占有できる体積が大きくなり(エネルギーはより大きな領域に分散される)、それに応じて、系がとりうる微視的状態の数が増加します。そのためWf > Wiとなり、膨張プロセスはエントロピーの増加を伴うことから(ΔS > 0)、自発的に起こります。
同様のアプローチで、熱の自発的な流れを説明することができます。熱い紅茶は、その熱エネルギーを周囲のより冷たい空気粒子に均等に分散させます。その結果、より多くの微視的状態が生じます。
エントロピーに関する一般論
エントロピー、微視的状態、および物質/エネルギー分散の間の関係により、物質の相対的なエントロピーに関する一般的な説明が可能になり、化学的および物理的プロセスにおけるエントロピー変化の兆候を予測することができます。
固相では、原子や分子は互いにほぼ固定された位置に制限されており、これらの位置に対してわずかに振動するのみです。そのため、系の微視的状態は比較的小さいです。液相では、原子や分子は、お互いに比較的近接しているにもかかわらず、互いの周りを自由に運動することができます。そのため、固体に比べて微視的な状態の数が多くなります。その結果、Sliquid>Ssolidと、物質が固体から液体に変わる過程(融解)は、エントロピーが増加する特徴があり、 ΔS > 0.となります。その結果、S液体>S固体となり、物質が固体から液体に変わる(融解する)過程は、エントロピーが増加するという特徴があり、 ΔS>0となります。 同様に、逆の過程(凍結)はエントロピーの減少、 ΔS <0 を示します。
気相 では、与えられた数の原子または分子が液相よりもはるかに大きな体積を占めており、これははるかに多くの微視的状態に対応します。その結果、どのような物質でも、S気体 > S液体 > S固体 と蒸発や昇華の過程も同様にエントロピーの増加を伴い、 ΔS > 0となります。同様に、相互の相転移—凝縮や凝固—はエントロピーの減少を伴い、 ΔS < 0となります。
分子運動論によると、物質の温度はその粒子の平均運動エネルギーに比例します。物質の温度を上げると、固体では粒子の振動がより大きくなり、液体や気体では粒子の並進がより速くなります。また、温度が高くなると、物質の原子や分子の運動エネルギーの分布も低温のときと比べより分散します。このため、物質のエントロピーは温度とともに増加します。
物質のエントロピーは、その物質を構成する粒子(原子や分子)の構造に影響されます。これは、粒子の質量と量子化された並進エネルギー準位の間隔との関係によるもので、原子の場合、重い原子は軽い原子よりも一定の温度で大きなエントロピーを持ちます。分子の場合、構成する原子の数が多いと分子の振動方法が増え、可能な微視的状態の数が増えることから、系のエントロピーが増加します。
最後のケースとして、粒子の種類の違いが系のエントロピーに影響を与える場合があります。すべての粒子が同じである純物質に比べて、2種類以上の異なる粒子が混在する混合物のエントロピーは大きいです。これは、同一でない成分で構成された系では、可能な配向や相互作用が増えるためです。例えば、固体が液体に溶けた場合、固体の粒子は運動の自由度が高くなり、溶媒の粒子との相互作用が増加します。これは、物質とエネルギーがより均一に分散し、微視的状態の数が増えることに対応しています。したがって、溶解の過程ではエントロピーが増加する( ΔS > 0)。
上記の文章は以下から引用しました。Openstax, Chemistry 2e, Chapter 16.2: Entropy.
