17.4:
Third Law of Thermodynamics
14,989 Views
•
•
A pure, perfectly crystalline solid possessing no kinetic energy (that is, at a temperature of absolute zero, 0 K) may be described by a single microstate, as its purity, perfect crystallinity,and complete lack of motion means there is but one possible location for each identical atom or molecule comprising the crystal (W = 1). According to the Boltzmann equation, the entropy of this system is zero.
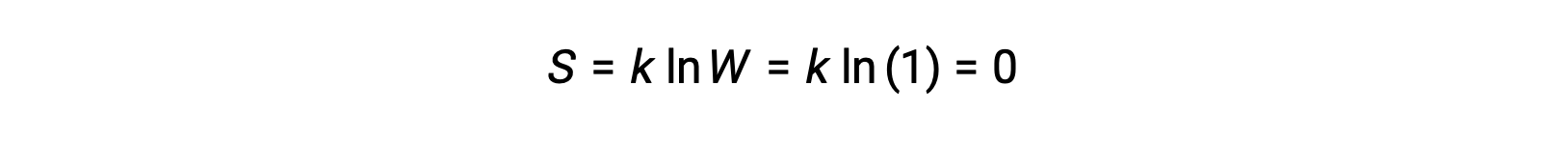
This limiting condition for a system’s entropy represents the third law of thermodynamics: the entropy of a pure, perfect crystalline substance at 0 K is zero.
Careful calorimetric measurements can be made to determine the temperature dependence of a substance’s entropy and to derive absolute entropy values under specific conditions. Standard entropies (S°) are for one mole of a substance under standard conditions. Different substances have different standard molar entropy values depending on the substance's physical state, molar mass, allotropic forms, molecular complexity, and extent of dissolution.
Due to the greater energy dispersal among the scattered particles in the gas phase, gaseous forms of substances tend to have much larger standard molar enthalpies than their liquid forms. For similar reasons, liquid forms of substances tend to have larger values than their solid forms. For example, S°H2O (l) = 70 J/mol·K and S°H2O (g) = 188.8 J/mol·K.
Among elements in the same state, the heavier element (larger molar mass) has a higher standard molar entropy value than the lighter element. For example, S°Ar (g) = 154.8 J/mol·K and S°Xe (g) = 159.4 J/mol·K.
Similarly, among substances in the same state, more complex molecules have higher standard molar enthalpy values than simpler ones. There are more possible arrangements of atoms in larger, more complex molecules, which increases the number of possible microstates. For example, S°Ar (g) = 154.8 J/mol·K and S°NO (g) = 210.8 J/mol·K despite the higher molar mass of argon. This is because in gaseous argon, energy takes the form of translational motion of the atoms, whereas in gaseous nitric oxide (NO), energy takes the form of translational motion, rotational motion, and (at high enough temperatures) vibrational motions of the molecules.
The standard molar entropy of any substance increases with increasing temperature. At phase transitions, such as from solid to liquid and liquid to gas, large jumps in entropy occur, which is due to the sudden increased molecular mobility and larger available volumes associated with phase changes.
This text is adapted from Openstax, Chemistry 2e, Chapter 16.2: The Second and Third Law of Thermodynamics.
