르샤틀리에의 원리: 온도 변화

질량 행동의 법칙에 따라, 농도의 변화에 의해 강조 평형은 평형 상수, K의가치에 변화없이 평형을 다시 설정으로 이동합니다. 그러나 온도 변화에 대응하여 평형이 변할 때, 평형 상수에 대해 상이한 값을 나타내는 상이한 상대 조성물로 재확립된다.

이 현상을 이해하려면 기본 반응을 고려하십시오.

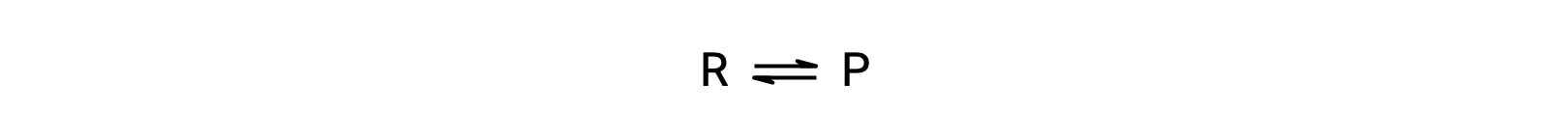
이것은 기본적인 반응이기 때문에, 전방 및 역에 대한 비율 법은 균형 잡힌 방정식의 stoichiometry에서 직접 파생 될 수있다 :

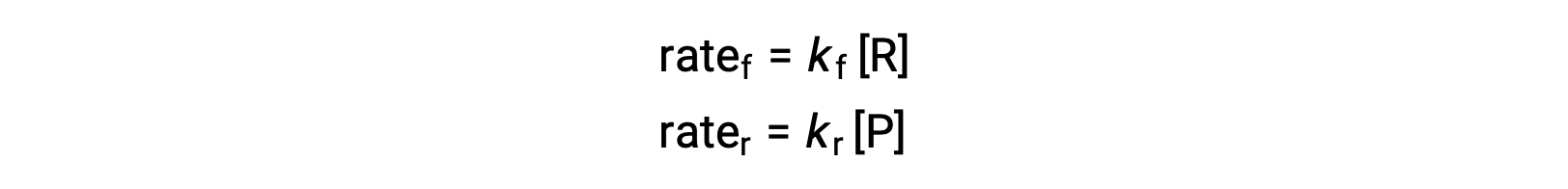
시스템이 평형상태일 때,

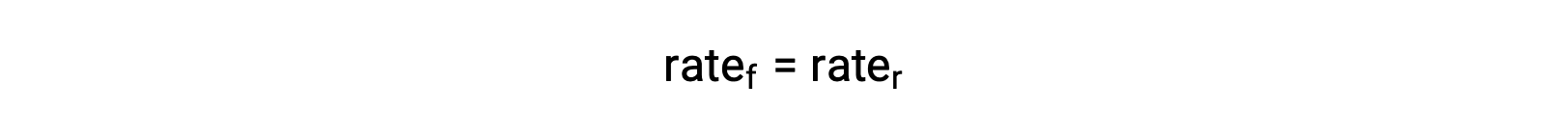
이 평등에 속도 법률을 대체하고 재배열은

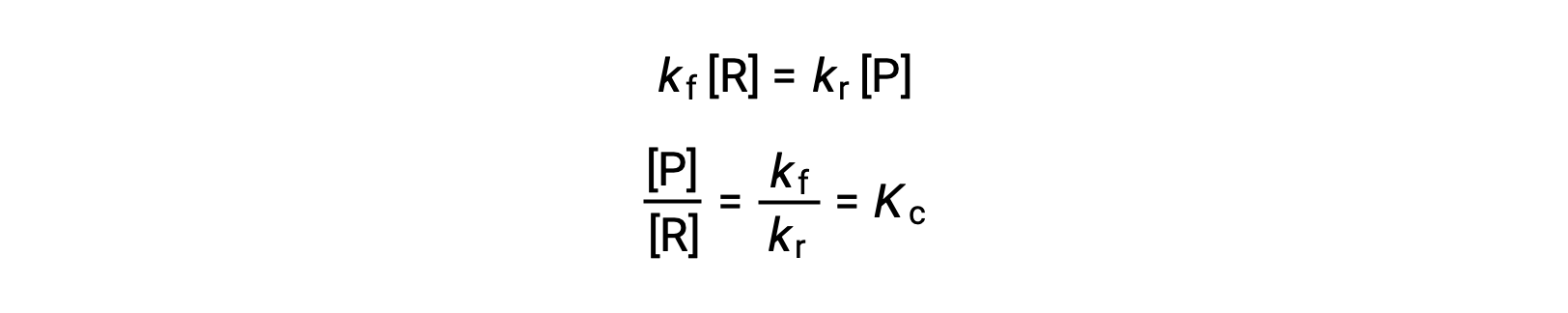
평형 상수는 전방 및 역반응에 대한 속도 상수의 수학적 함수로 표현될 수 있다. 속도 상수는 Arrhenius 방정식에 의해 설명된 것과 같이 온도에 따라 다르기 때문에 평형 상수가 온도에 따라 달라질 것이라는 추론을 의미합니다(온도 변화에 의해 상수가 다른 정도에 영향을 받는다고 가정). 다단계 반응 메커니즘을 포함하는 더 복잡한 반응의 경우, 평형 상수와 메커니즘내 단계의 속도 상수 사이에 유사하지만 더 복잡한 수학적 관계가 존재한다. 반응이 얼마나 복잡하든, 평형 상수의 온도 의존도가 지속됩니다.

온도 변화에 대응하여 평형이 경험하게 될 변화를 예측하는 것은 반응의 엔탈피 변화를 고려하여 가장 편리하게 달성된다. 예를 들어, Haber의 공정에 의한 암모니아 형성은 다음과 같은 외형 (열 생산) 과정입니다.

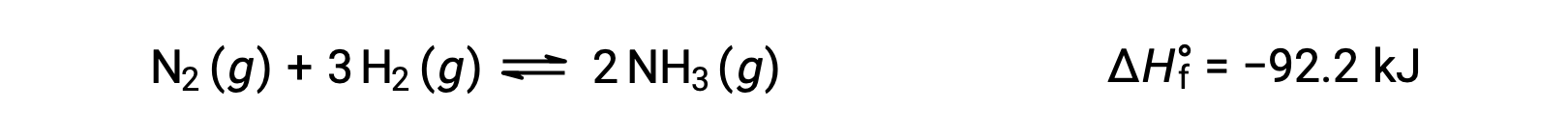
Le Châtelier의 원칙을 적용하기 위해 열, q는제품으로 간주될 수 있습니다.

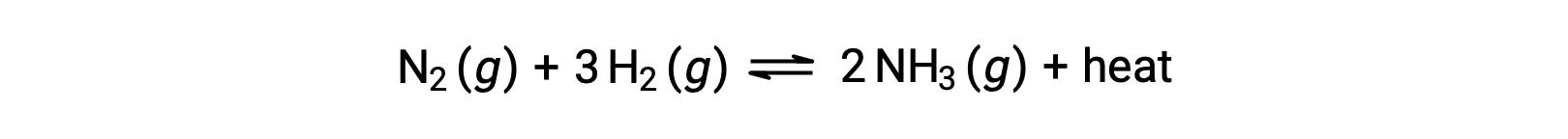
시스템의 온도를 올리는 것은 제품의 양을 증가하는 것과 비슷하므로 평형이 왼쪽으로 이동합니다. 시스템 온도를 낮추면 평형이 오른쪽으로 이동하게 됩니다. 벤더믹 공정의 경우, 열은 반응의 반응으로 간주되므로 반대 온도 의존도가 관찰됩니다.

이 텍스트는 Openstax, 화학 2e, 섹션 13.3 변속 평형에서 적응되었습니다: Le Châtelier의 원리.