アレニウスプロット

アレニウス式は、化学反応の活性化エネルギーと速度定数kを関係付ける式です。アレニウス式は、k = Ae^−Ea/RTと表されます。ここでRは気体定数であり、その値は8.314 J/mol·K、Tは絶対温度、E_aは活性化エネルギー（J/mol）、eはネイピア数(2.7183…)、Aは頻度因子と呼ばれる定数で、衝突の頻度や反応する分子の向きなどに関係します。

アレニウス式は、実験データから反応の活性化エネルギーを計算するために使用することができます。ある反応のE_aを決定する便利な方法は、2つ以上の異なる温度でkを測定することです。この方法では、一次方程式に変形したアレニウス式を使用します。

 

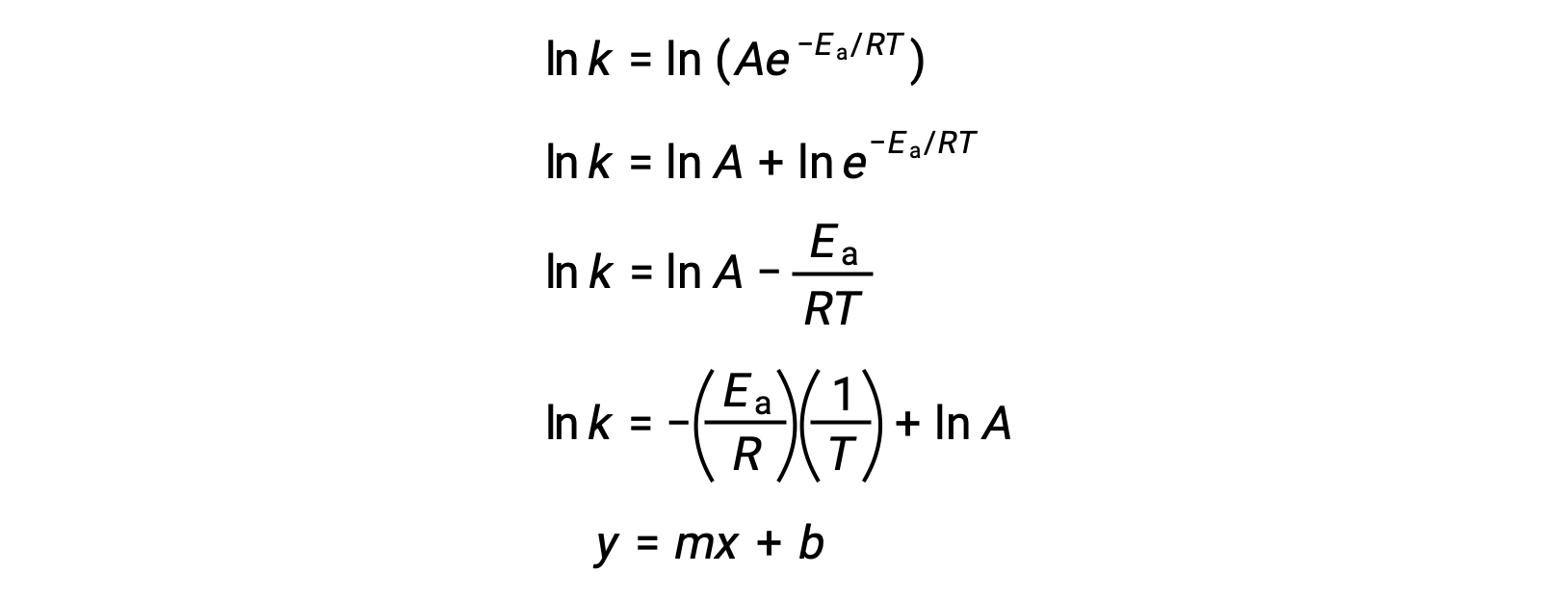
ln k対1/Tのプロットは、傾きが −E_a/Rに等しく、y切片が ln Aに等しい直線となります。

以下の反応を考えると、

 

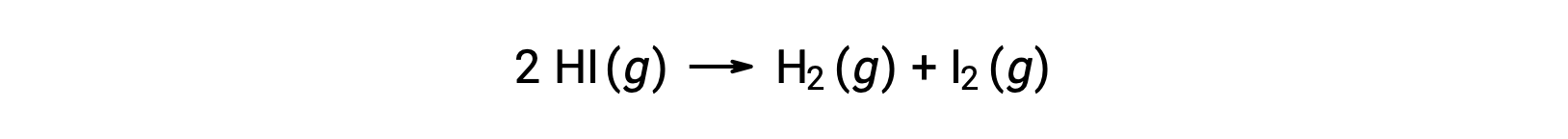
この反応の活性化エネルギーは、図を参考に反応速度データを用いて、速度定数の温度による変化がわかれば求めることができます。

絶対温度 (K)	反応速度定数 (L/mol/s)
555	3.52 × 10–7
575	1.22 × 10–6
645	8.59 × 10–5
700	1.16 × 10–3
781	3.95 × 10–2

与えられたデータを用いると、温度の逆数（1/T）とkの自然対数（ln k）の値を導き出すことができます。

1/T (K–1)	ln k
1.80 × 10–3	–14.860
1.74 × 10–3	–13.617
1.55 × 10–3	–9.362
1.43 × 10–3	–6.759
1.28 × 10–3	–3.231

 

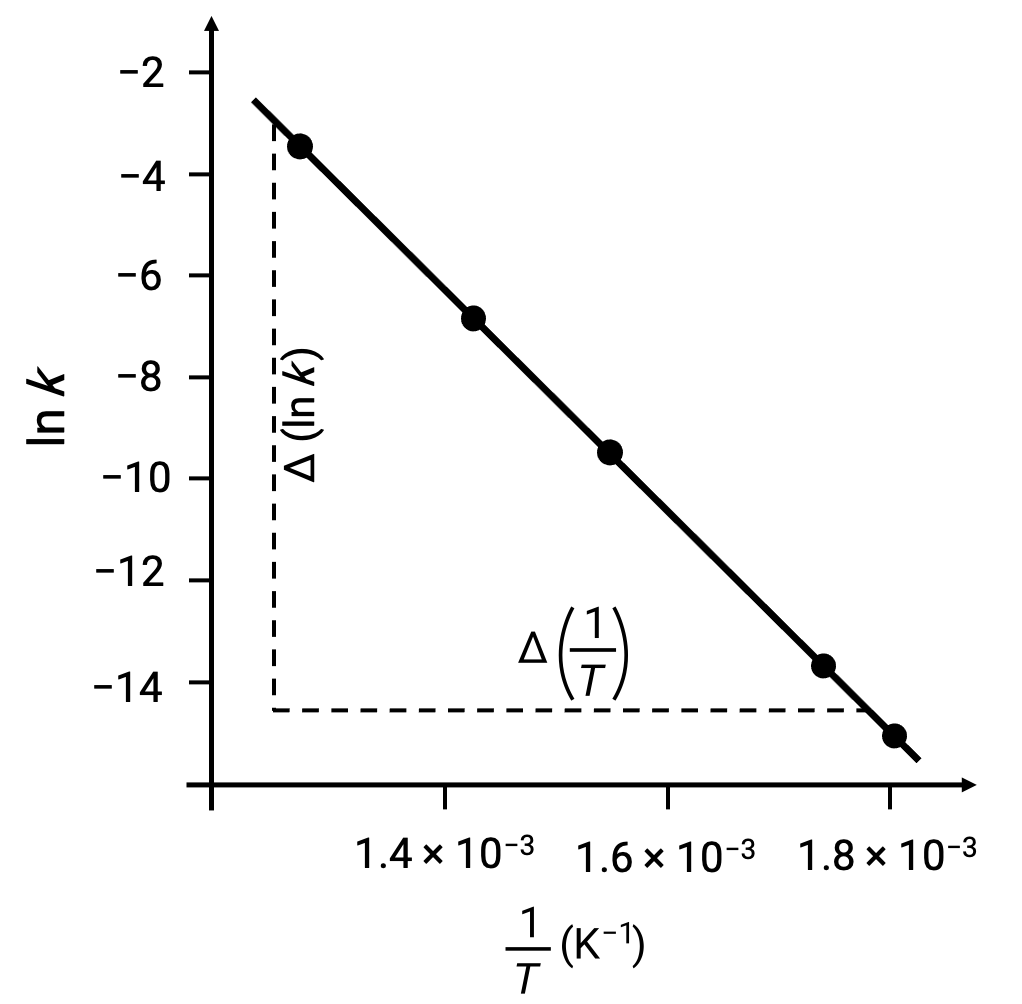
導き出されたデータ点をln k vs. 1/Tでプロットすると、図のようにln kと1/Tの間に直線的な関係を示す線図が生成されます。

活性化エネルギーに相当する直線の傾きは、2つの実験データのいずれかを用いて推定することができます。              

 

活性化エネルギーを導出する別の方法として、2つの異なる温度での速度定数を利用する方法があります。この方法では、アレニウス方程式を2点間の直線式に並べ替えます。

 

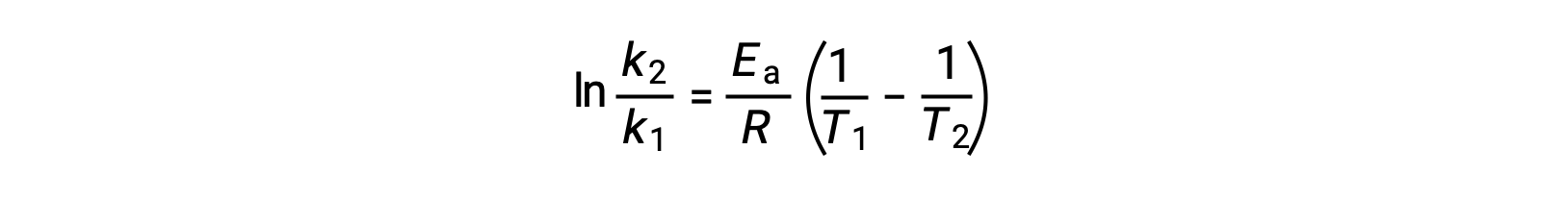
式を並べ替えると、活性化エネルギーの式となります。

 

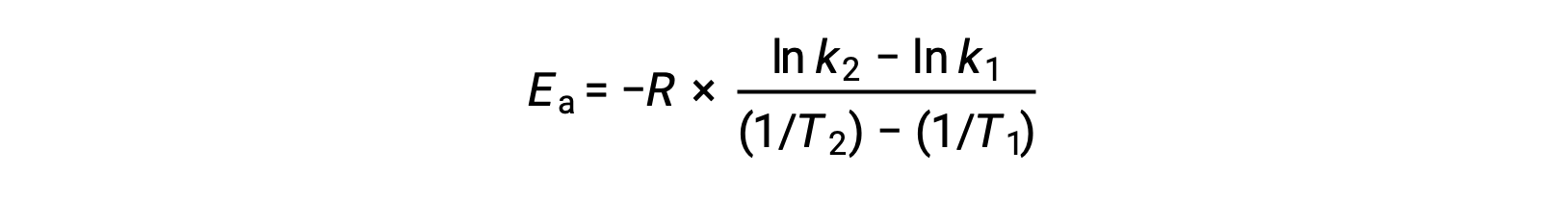
任意の2つのデータを代入してさらに計算すると、活性化エネルギーの値がJ/molまたはkJ/molで得られます。

 

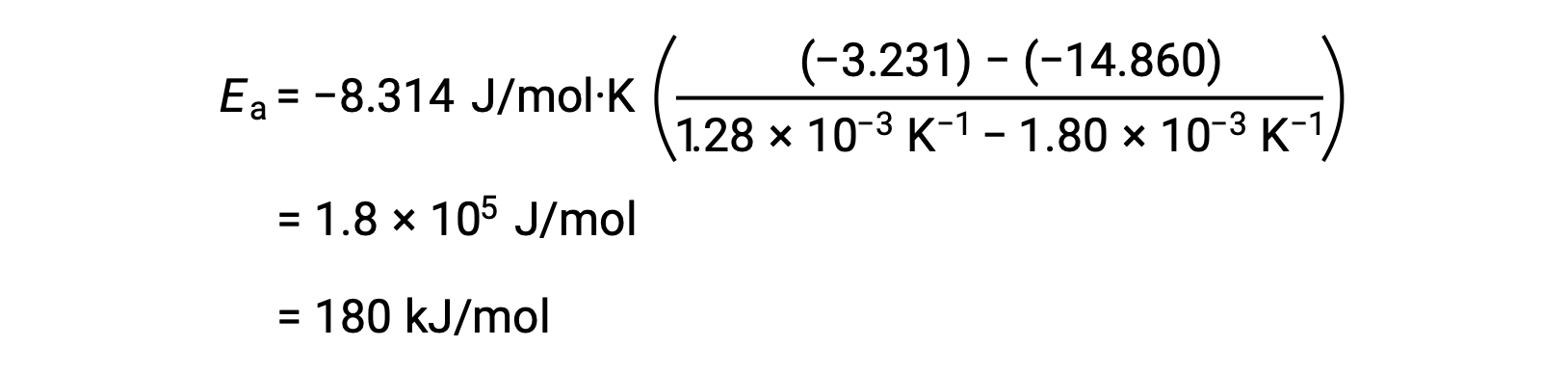
この代替となる2点法は、グラフを用いる方法と同じ結果をもたらします。しかし、実際の実験データを扱う際には、グラフを用いる方法の方がより信頼性の高い結果を得ることができます。

上記の文章は以下から引用しました。Openstax, Chemistry 2e, Section 12.5: Collision Theory.