17.4:
열역학 제3법칙
14,662 Views
•
•
순수하고 완벽하게 결정체가 없는 운동 에너지(즉, 절대 0, 0 K의 온도)는 단일 마이크로스테이트에 의해 설명될 수 있으며, 순도, 완벽한 결정성, 그리고 완전한 운동 부족으로 결정(W=1)을 포함하는 각각의 동일한 원자 또는 분자에 대해 하나의 가능한 위치가 있음을 의미한다. Boltzmann 방정식에 따르면,이 시스템의 엔트로피는 0입니다.
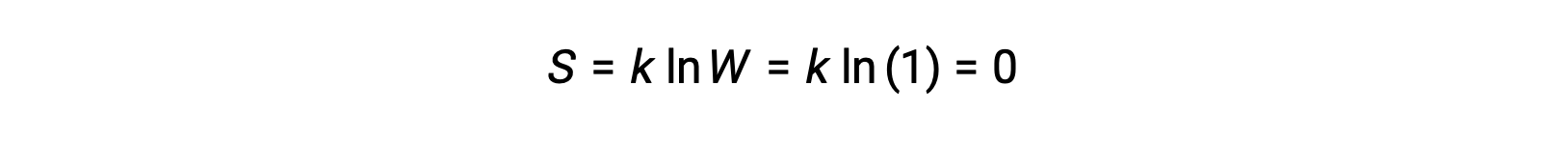
시스템의 엔트로피에 대한이 제한 조건은 열역학의 세 번째 법칙을 나타냅니다 : 0 K에서 순수하고 완벽한 결정성 물질의 엔트로피는 0입니다.
신중한 칼로리 측정은 물질의 엔트로피의 온도 의존성을 결정하고 특정 조건하에서 절대 엔트로피 값을 도출하기 위해 이루어질 수 있습니다. 표준 엔트로피(S°)는표준 조건하에서 물질의 한 두더지용입니다. 다른 물질은 물질의 물리적 상태, 어금니 질량, 동색 형태, 분자 복잡성 및 용해 정도에 따라 다른 표준 어금니 엔트로피 값을 가지고 있습니다.
가스 상에서 흩어져 있는 입자 들 사이에서 더 큰 에너지 분산으로 인해, 기체 형태의 물질은 액체 형태보다 훨씬 더 큰 표준 어금니 엔탈피를 갖는 경향이 있다. 비슷한 이유로, 물질의 액체 형태는 그들의 고체 형태 보다 더 큰 값을 가지고 하는 경향이. 예를 들어, S°H2O(l) = 70 J / mol· K 및 S°H2O(g) = 188.8 J /mol·K.
동일한 상태의 요소 들 중, 무거운 요소 (더 큰 어어 질량) 가벼운 요소 보다 더 높은 표준 어금니 엔트로피 값을 가지고. 예를 들어, S°Ar(g) = 154.8 J / mol· K 및 S°Xe(g) = 159.4 J / mol·K.
유사하게, 같은 상태에 있는 물질 중, 더 복잡한 분자는 간단한 그들 보다는 더 높은 표준 어반실값을 가지고 있습니다. 더 크고 복잡한 분자에서 원자의 더 많은 가능한 배열이 있어 가능한 미세 상태의 수가 증가합니다. 예를 들어, S°Ar(g) = 154.8 J / mol· K 및 S°NO(g) = 210.8 J / mol · 아르곤의 더 높은 어금니 질량에도 불구하고 K. 이는 기체 아르곤에서 에너지가 원자의 번역 운동 형태를 취하는 반면, 위산화물(NO)에서는 에너지가 분자의 번역 운동, 회전 운동 및 (고온에서) 진동 운동의 형태를 취하기 때문입니다.
어떤 물질의 표준 어금니 엔트로피는 온도 가 증가함에 따라 증가합니다. 고체에서 액체, 액체로 가스로 의위상 전이에서 엔트로피의 큰 점프가 발생하며, 이는 급격한 분자 이동성 증가및 위상 변화와 관련된 더 큰 사용 가능한 부피 때문입니다.
이 텍스트는 Openstax, 화학 2e, 제 16.2 장: 열역학의 두 번째 및 세 번째 법칙에서 채택됩니다.
