Three-Dimensional Particle Shape Analysis Using X-ray Computed Tomography: Experimental Procedure and Analysis Algorithms for Metal Powders

Edward J. Garboczi; Nik Hrabe

doi:10.3791/61636

JoVE Journal > Engineering

Engineering

Three-Dimensional Particle Shape Analysis Using X-ray Computed Tomography: Experimental Procedure and Analysis Algorithms for Metal Powders

Published: December 04, 2020

doi:

10.3791/61636

Edward J. Garboczi¹, Nik Hrabe¹

¹Applied Chemicals and Materials Division, MS647,National Institute of Standards and Technology

Summary

The size and shape of powder particles are not independent quantities. Usual measurement techniques do not measure these intertwined parameters in three dimensions (3D). A 3D measurement/analysis technique is described, based on X-ray computed tomography, which can measure size and shape and classify powder particles according to both parameters.

Abstract

Measuring the size distribution of the particles in a powder is a common activity in science and industry. Measuring the shape distribution of the particles is much less common. However, the shape and size of powder particles are not independent quantities. All known size/shape measurement techniques either assume a spherical shape or measure the shape in two dimensions only. The X-ray computed tomography (XCT) based method presented here measures both size and shape in 3D without making any assumptions. Starting from a 3D image of particles, the method can mathematically classify particles according to shape, for example particles composed of several smaller particles welded together as opposed to single particles that are not necessarily spherical. Of course, defining a single number as the "size" or "shape" of a random non-spherical particle is not possible in principle, leading to many ways to estimate particle size and shape via various interlinked parameters, which can all be generated from this complete 3D characterization in the form of averages and distributions. The necessary experimental procedures, mathematical analysis, and computer analysis are described and an example is given for a metal powder. The technique is limited to particles that can be imaged by XCT with a minimum of about 1000 voxels per particle volume.

Introduction

Measuring the size distribution of the particles in a powder is a common activity in science and industry¹^,². Measuring the shape distribution of the particles is less common, but both size and shape, along with the material the particles are made from, determine their properties, either alone or in some kind of matrix material³^,⁴^,⁵^,⁶^,⁷. Materials whose particle size and shape are of interest include portland cement, sand, and gravel⁸^,⁹^,¹⁰^,¹¹^,¹²^,¹³^,¹⁴^,¹⁵^,¹⁶^,¹⁷^,¹⁸^,¹⁹^,²⁰^,²¹^,²²^,²³, metal powders for powder metallurgy and additive manufacturing²⁴^,²⁵^,²⁶, lunar soil²⁷^,²⁸^,²⁹, shredded automotive tires³⁰, crushed waste glass³¹, stem cells³², and carbon nanotubes and graphene³³^,³⁴^,³⁵^,³⁶^,³⁷. However, the shape and size of powder particles are not independent quantities²⁶. For example, suppose one has a geometrically regular particle whose "size" is said to be d. Without saying whether this particle is a sphere, a cube, or a thin rod of length d, one does not really know how the size applies to this particle. By saying that the particle is a sphere, cube, or rod, one is really specifying the particle's shape, and without this extra information, the size information is meaningless.

For these three examples, a sphere, cube, or thin rod, particle size can be specified by a single number. But even if the rod had a circular cross-section, one would need to also measure the diameter of this cross-section, so two size parameters would really be needed for the thin rod particle. What about particles shaped like ellipsoids, or rectangular boxes? For each of these, three numbers are needed to specify the size, and still the shape must be given as either an ellipsoid or a rectangular box in order for the three size parameters to have meaning. For a randomly-shaped particle, an infinite number of size parameters (e.g., the length of chords across the particle) would be needed to completely characterize the "size" of the particle, and yet these would be meaningless without a "shape characterization," knowing at what angles relative to the center of mass of the particle these chords were drawn.

There are many techniques used for measuring the size distribution of the particles in a powder, employing different physical principles¹^,². What is not usually recognized, however, is that in order to extract particle size, information about particle shape, whether assumed or measured, must be used. Current techniques can be classified as: (I) measurements of three-dimensional (3D) particle size while assuming 3D shape, and (II) measurements of both size and shape but only of two dimensional (2D) projections, using 2D image analysis techniques. For spherical particles, all 2D projections are circles, with the same diameter as the original particles, and all these measurement techniques, both Class I and Class II, within measurement uncertainty, give the same results for perfect spheres. For non-spherical particles, the 2D projections are much less closely related to the original particles. If a particle has internal porosity that does not break the particle surface, these pores will not be measured at all by any of these 3D or 2D measurement techniques. Class I includes laser diffraction, electrical sensing volume (ESV)³⁸, sieve analysis, and sedimentation; and Class II covers transmission and scanning electron microscopy, atomic force microscopy, and dynamic and static image analysis with optical techniques. Neither class accurately measures the size and shape of non-spherical particles in 3D.

Since around 2002³⁹, a new method of particle analysis has been developed⁴⁰^,⁴¹^,⁴²^,⁴³^,⁴⁴^,⁴⁵ that images a 3D particle in 3D, and then uses several forms of mathematical analysis to represent and classify each particle. A 3D image is saved for each individual particle, which can be compared to the geometrical and mathematical information that is also saved for each particle. This mathematical information can be used to re-generate the particle as desired in any kind of 3D model⁴⁶^,⁴⁷^,⁴⁸^,⁴⁹, at any location and orientation, or to generate virtual particles that are forced to have the same statistics⁵⁰^,⁵¹. This particle analysis method is based on XCT scans of particles dispersed in epoxy or some other such medium. The XCT scans are operated on by specialized software that employ the burning algorithm⁵²^,⁵³^,⁵⁴^,⁵⁵^,⁵⁶ to identify particles, and then either spherical harmonic series fitting or voxel counting to generate and store particle shape and size, 3D images of the particles, and, in a second step, geometrical information for each particle. Each particle analyzed has a unique alphanumeric label, which is used to track each particle, the information about each particle, and link each particle to its 3D image. During this analysis process, pores that are inside a particle are analyzed and the total porosity in that particular particle is stored, since XCT reconstruction gives a complete 3D view of a sample.

Three (out of many) geometrical size/shape parameters have been found to be particularly useful in analyzing and classifying particles in 3D: the length, L, the width, W, and the thickness, T. L is defined as the longest surface point to surface point distance across a particle, W is defined similarly as L with the additional constraint the unit vector along W must be perpendicular to the unit vector along L, and T is also defined similarly as L with the additional constraint that the unit vector along T must be perpendicular to both the unit vector along L and the unit vector along W¹². These three parameters define the minimum rectangular or bounding box that just contains the particle, and the ratios of these three parameters give valuable but approximate shape information about each particle. Distributions can be made of any of these. It is possible that W correlates well with the "sizes" measured with sieve analysis⁵⁷, while the "sizes" measured with laser diffraction correlate to a mixture of L, W, and T³¹.

Finally, the 3D images of a test sample of 100-200 of the particles are visually checked to determine where the cutoffs in L/T are that enable the method to distinguish between single, near-spherical (SnS) particles, and non-spherical (NS) particles, which could be multiple particles welded together, or what are clearly single particles but with an odd shape.

Protocol

NOTE: The following protocol is written for metal powder particles with size, according to a volume-equivalent spherical diameter (VESD, diameter of sphere with same volume as particle) approximation, between 10 µm and 100 µm. Assume that the metal has a density in units of g/cm³. Gloves should be worn during the sample preparation steps, along with eye protection. It is important to read over all the steps in Protocol 1, as some equipment needs to be ready before starting the Protocol.

1. Preparation of the epoxy-powder mixture

Prepare approximately 25 g of a quick-curing (5 min) epoxy in a small disposable dish. Aluminum foil boats work well for this purpose. A good epoxy to use comes in a bubble wrap, with the resin separated from the hardener, whose cured density is ρ_e g/cm³.
Use M grams of the powder, from a well-shaken larger sample of powder, where M is designed to give a volume fraction of about 10% once the M grams are mixed into the epoxy. This is designed to avoid the situation where particles are so near to each other that the XCT scan wrongly identifies them as real multi-particles that are firmly attached. The equation defining M is:
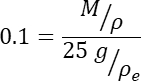
Mix the metal powder vigorously into the epoxy, manually, using a disposable stirring rod – a simple wooden craft stick works fine – for about 30 s, long enough to disperse the powder adequately. This process, done well, makes the image analysis of the individual particles much more straightforward.
1. After mixing, scrape the viscoplastic mixture into a compact clump with as much vertical extent as possible, to be ready for the next step. It is important to have the following steps prepared ahead of time, as there will not be much time left before the epoxy hardens.
Use a small vacuum pump connected to an 0.5 m long plastic hose, with a nozzle inserted in the open end of the hose that will fit snugly into a polymer straw of about 3 mm interior diameter.
NOTE: Cocktail straws, easily available in grocery stores, work well for the 3 mm diameter polymer straw and have a length of about 150 mm. For a nozzle, the cut-off end of a disposable 1 mL to 2 mL plastic pipette usually is effective. Where the nozzle fits into the plastic hose, some electrical tape should be stretched tightly around the joint to ensure an airtight seal. The 25 g of epoxy plus powder should be more than enough to fill two complete straws.
Insert the nozzle into the straw, holding the nozzle and the straw end firmly pinched together. Insert the free end of the straw into the compact epoxy-powder clump and turn on the vacuum pump.
NOTE: Keep the free end of the straw immersed in the epoxy-powder mixture to avoid introducing air bubbles into the straw – some air bubbles will always be present, but this procedure minimizes their presence. The straws should be filled to within 10 mm from the top – the fill line can be seen through the translucent straw. When the first straw is filled, turn off the vacuum pump and remove the straw from the nozzle.
Wipe off the epoxy mixture from the filling end of the straw and push both ends of the straw into a small lump of clay in order to fill both ends of the straw so that no epoxy-powder mixture leaks out during curing. Place the 2^nd straw on the nozzle and repeat, first using the mixing rod to gather the epoxy-powder mixture together if necessary.
After the epoxy in the two straws is cured, cut off the straw ends, where the clay sealer was, with a razor and then cut each straw in half to give four samples. Use one straw as sample #1 for the XCT, mounted vertically so that the X-rays will penetrate across the circular cross-section of the straw.

2. The XCT instrument

NOTE: These steps assume familiarity with the XCT instrument chosen by the user.

Use a high voltage, usually 100 kV or higher, as there is good contrast between the epoxy matrix and the metal powder particles and there is no need to resolve anything inside the epoxy matrix, which would normally require low voltages around 40 kV. Use a full 360^o scan, with a voxel size of about 1 µm. The ratio between the smallest particle size considered and the voxel size used should be a minimum of 8-10³⁹.
Take enough FOVs, over more than one sample, to give enough particles for analysis. If the sample preparations guidelines are followed, 2 to 8 FOVs will be sufficient. Typically, a minimum of 1000 particles is enough for a valid shape/size analysis, but more particles result in smoother distribution curves and better statistics. The reconstructed slices are numbered from 0 to nz-1, from bottom to top of the FOV, where nz is the total number of reconstructed slices.
1. Save the vertical cross-section slices for each FOV individually, in 8bit format (e.g., tiff) noting the pixel size of each image set (nx x ny), the number of these slices (nz), and the voxel size in micrometers (v). 8bit format is adequate for these kinds of simple metal particle-epoxy matrix gray scale images, which are easy to segment.

3. Assembly of the slices belonging to each FOV into a 3D ASCII microstructure

NOTE: The C program that is used at NIST is called tiff2array.c and is most often used with tiff files but can handle other 8bit formats. It can be compiled as is, with the executable named tiff2array. This program reads in each image, from the bottom up, converts them into ascii format (0 to 255 gray scale) and then stacks them at the end of a master file.

If the reconstructed images are in tiff format, for example, and are numbered consecutively from the bottom up, use the following syntax in a line terminal command: tiff2array *.tiff. This master file, or microstructure file, is a 3D representation of the FOV. If the variable a(i,j,k) is the gray scale at position (i,j,k), where k is the number of the slice, k = 1 to nz, and (i,j) is the pixel in the kth slice, where i is measured from left to right and j is measured from top to bottom.
NOTE: All software needed in the Protocol is available in the Supplemental Information section of this paper via a link to a NIST database located at https://doi.org/10.18434/M32265.
For P FOVs, make a small file called particle-class-sysconfig.dat, with P lines, where each line reads, for the pth (p=1,P) FOV:
Filename nx ny nz v b c
where Filename = a 12-character identification for a particular FOV, b = 1 for an interior scan and 0 for an exterior scan, and c = the number of phases present in the images. When an interior scan is done, there are usually three (c=3) phases present: 1) the epoxy, 2) the black regions indicating the outside of the circular scan and air bubbles, and 3) the brighter particles. Sometimes four phases might appear to the eye to be a more reasonable assumption and so c = 4. Values for c of 3 or 4 are the only two choices. The value of c tells the particle analysis software which Otsu automatic segmentation algorithm, originally written for two-phase images but easily extended to any number of phases, to use to automatically segment the images in a particular FOV²⁶^,⁵⁸. The microstructure files that will be used in the next software program must have 12-character names that are exactly the same as the Filename listed in the FOV-name-sysconfig.dat file, followed by the extension .mic.
Run the particle analysis software pp-Otsu.f, using as input the particle-class-sysconfig.dat file and the various microstructure files, Filename.mic. Make only two changes to this program for a new system, all of which are marked by a comment "USER" in the Fortran source: the filenames for the general output files (change the general particle class name) and the number of FOVs listed in particle-class-sysconfig.dat. The program pp-Otsu.f is in Fortran, is scalar, and is usually compiled in Fortran 77, although Fortran 90 should work fine. It, and all other Fortran programs described below, should be compiled in double precision (-r8) for accurate results.
1. In addition, since pp-Otsu.f works with large files, always add the parameters (or their equivalent) -mcmodel=medium and -Mlarge_arrays to the compilation. An auxiliary file, gauss120.dat, contains the weights and points for a 120-point Gaussian quadrature used extensively in pp-Otsu.f, and must be in the same directory as pp-Otsu.f. All the programs described below are written in Fortran 77 except for the MPI programs, which are written in Fortran 90.
View the particle files that are the main outputs from pp-Otsu.f, which can take several hours to run on a single processor if there are thousands of particles to be analyzed. These include files with names such as Particle-class-name-anm-particle-number.dat, which contain the list of the complex coefficients (n = 0,26), with units of micrometers or in whatever units v is, for the particles judged to be adequately star-shaped³⁹ and thus capable of being expanded in spherical harmonics functions (called SH particles). Particle files also include files like Particle-class-name-part-particle- number.dat, which contain the number of voxels in the particle and all the voxel positions (in voxel coordinates) for particles that are not capable of being described by spherical harmonic expansions (called nonSH particles).
View the two files, one for the SH and one for the nonSH particles, which give the porosities of all the particles found, even if the porosity is zero, with the phrase porosity in the filenames. An additional program, porosity-analyze.f, should be given the number of lines in each porosity file and their filenames – the file names to be changed are at the beginning of the source code. The output from this program are the two files Particle-class-intern-poros-analysis.txt and Particle-class-intern-poros-list.txt. The analysis file generates the information shown in Table 2 in the Representative Results section, and the list file gives the information needed to generate Figure 5 in the Representative Results section.
View the three tiff image files showing one slice of the first FOV considered. The first slice (OriA-0500.tiff) shows the k = 500 slice of the first FOV in the particle-class-sysconfig.dat file, without any image processing, and the second image file shows the same image but now segmented and thresholded (PixA-0500.tiff). If any limited watershed splitting is applied, then the third image file shows the results of this algorithm (LWSA-0500.tiff). Usually this image processing step is not applied, so the third image file is the same as the second. These images are generated as an error-checking step on the original assembly of the 3D microstructure and the automatic Otsu image segmentation. A general output file (particle-class-name-particles-data.dat) is created listing all the auxiliary information for the processing of each particle. This file is only used as a reference, but the voxel volumes and number labels of all particles processed are written at the end of this file.
For each processed particle, whether SH or nonSH, view the 3D VRML image file, with naming convention particle-name-particle-number.wrl. For SH particles, this VRML image file contains two images side-by-side, a voxel image of the original particle, and a smoother rendered image using the SH coefficients. For the nonSH particles, only the voxel image is stored.

4. Generate geometrical information for all SH and nonSH particles

Prior to further processing, make a list of the Particle-class-name-anm-particle-number.dat file names, called anm.lis, and a list of the nonSH Particle-class-name-part-particle-number.dat particles, called nonSH.lis. Run the small program number.f, having first been edited to have the correct number of files in anm.lis. This changes the anm.lis file to have the number of the particle on each line of the list file, as well as the filename, replacing the previous file.
Use the program part-lwt-listnum-unitvector.f to generate and evaluate geometrical information for the SH particles. This is an MPI parallel program, since there can be thousands of SH particles to be evaluated, and only doing one particle at a time can take days. The only changes in this program that need to be made when processing a new particle class are the Ntot number of Particle-class-name-anm-particle number.dat files, and the particle class naming information for the output (Particle-class-name-un-geom-len.dat) file. The program has comments (USER) at the few places that need to be changed for a new particle type. The output file Particle-type-info-un-SH-geom-len.dat unites particles from every FOV, and each line has the following structure.

SH coefficients filename, x1, x2, y1, y2, z1, z2, volume, surface area, SA ratio, curv, ratio, nnn, gauss, placeholder, L, W, T, L/T, W/T, T/T, moment of inertia tensor components, L unit vector, theta, phi angles, W unit vector, theta, phi angles, T unit vector, theta, phi angles

x1 is the minimum x value on the surface of the particle and x2 is the maximum and similarly for y and z. These define an "extent box" that just encloses the particle in its as-measured orientation⁴². The extent box is used in other applications⁴⁶^,⁴⁷^,⁴⁸^,⁴⁹. SA ratio is the surface area of the particle divided by the surface area of the volume-equivalent sphere. Curv is the integrated mean curvature inverted and normalized so that it is equal to the diameter when the particle is a perfect sphere. Ratio is the trace of the moment of inertia tensor divided by the trace of the moment of inertia tensor for the volume-equivalent sphere. nnn is the maximum number of SH coefficients (n=0, nnn) that should be used when working with the given particle. Gauss is the integrated Gaussian curvature, divided by 4π, which should equal 1 for a closed object. The point at which Gauss varies from unity by more than 5% defines the maximum number of SH coefficients (n= nnn) that should be used when recreating the particle. L, W, T are the length, width, and thickness of the particle, and were defined in the Introduction section. The independent components of the moment of inertia tensor are listed as I₁₁, I₂₂, I₃₃, I₁₃, I₂₃, I₁₂. Finally, the unit vector for L is listed, in the order of the x,y, and z coordinates, followed by the spherical polar angles θ (angle from the positive z-axis) and Φ (angle of rotation around the z-axis, defined to be zero at the positive x-axis and is positive counter-clockwise). The parameters for W and T follow, listed in the same way.
Use the program nonSH-lwt-un-scalar.f to compute the L, W, and T parameters for the nonSH particles, operating on the nonSH.lis list of filenames, and also record the associated unit vectors. The only changes that need to be made in this file for a new particle class is the number of filenames in nonSH.lis, and the output filenames. The main output from this program, named Particle-name-info-nonSH-len.dat, has each line in the format:

Filename volume L W T a1 a2 a3 (LWT unit vectors and angles)

where a1, a2, and a3 are the final angles (in degrees – 90^o) between the unit vectors for L and W, W and T, and L and T, which are included as an error check for the L, W, and T computation algorithm, since these angles should all be zero for a perfect computation. The L, W, and T unit vectors and angles are in the same format as for the SH particles.

5. Select a subset of SH and nonSH particles to visually determine SnS and NS L/T cutoffs

NOTE: The SH particles, in general, comprise single spherical particles, single non-spherical (ellipsoidal or broken in some way or else a random shape) particles, double particles, and multiple (more than two particles joined together) particles. The particles making up the multiple particles can be spherical or non-spherical. The nonSH particles generally have a few single spherical particles, although mainly with large pores that have broken through to the surface, and the rest are mostly double and multiple particles²⁶. This is determined by viewing a random sample of both kinds of particles with values of L/T from 1 to 2. Such a visual inspection becomes an important step to enable the SnS and NS classification.

Run program (VRML-select-multi-single.f) that reads the Particle-type-info-SH-geom-len.dat and Particle-name-info-nonSH-len.dat files, and picks out 10 particles in each L/T interval of size 0.1, i.e., (1,1.1), (1.1,1.2), etc. This stores up to 100 SH particles with L/T ranging from 1 to 2, and up to 100 nonSH particles with the same L/T range. Two text files are generated (*SH-VRML-list.txt and *nonSH-VRML-list.txt) listing the L/T values and the root names of the VRML image files found. These should be put into a spreadsheet of some kind and ordered according to the L/T value.
Examine the 3D images of each of these particles visually to determine the overall range of morphologies, starting from the lowest L/T value particles. The particles are assessed in terms of whether they are broken particles, double particles, multiple particles, irregular (e.g., not very spherical), and whether they have satellites, which are much smaller particles, attached to the main particle. A satellite is judged to make the main particle a double or multiple particle if the satellite(s) are more than 1/5 the diameter of the main particle. The approximate value of L/T is found that separates single, near-spherical (SnS) particles from multiple and very non-spherical particles (NS), which can be a bit different for the SH and nonSH particles. The first double or multiple particle found determines the cutoff value for both SH and nonSH particles.
NOTE: The Supplementary Material, located at https://doi.org/10.18434/M32265, includes a spreadsheet file for the particles examined, to see how these cutoff values were determined. There is some uncertainty and a degree of subjectivity in these numbers, which can be assessed by choosing a different set of 100 SH and 100 nonSH particles, with L/T between 1 and 2, to evaluate the cutoff values. Recent work found that this uncertainty was small²⁶ and did not affect the results significantly.

6. Generate 2D projection data from the 3D particles

NOTE: The only current commercial particle analyzers that measure particle shape at all do so with 2D projections. The XCT data can be analyzed to give arbitrary 2D projections, generating data that can be quantitatively matched to the results of these commercial instruments. The 2D projections are made from both the SH and nonSH particles and are combined, with no attempt to classify into 2D SnS and NS categories, since it is not known at present how to define these classes for 2D projections.

Use the two programs, (proj-mpi-SH-LWT.f) for the SH particles and (proj2D-nonSH-LWT.f) for the nonSH particles, to generate three orthogonal projections for each particle, along the direction of the three LWT unit vectors, and then generate Fourier coefficients for the outline of the projection. These coefficients are used to compute various 2D quantities such as area, perimeter, and various lengths and aspect ratios.
A series of (x,y) points are generated and stored for each projection, labelled with the particle file name and 1 for the projection along the L unit vector, 2 for the projection along the W unit vector, and 3 for the projection along the T unit vector. Input these into any graphing program that accepts this input, making sure that the axis limits of x and y should be the same, and each axis is the same physical length.
Store the Fourier coefficients with a similar file naming convention, but this feature is turned off, by default, using comments. The only changes made in either of these programs (program position marked with "USER") is the total number of particles to be considered (Ntot), and the input and output filenames, which should reflect the particle class being analyzed.
The main output from running (proj-mpi-SH-LWT.f) and (proj2D-nonSH-LWT.f) are projection data files, with naming convention Particle-class-info-SH-proj.dat and Particle-class-info-nonSH-proj.dat. A variety of 2D quantities can be computed, including some used by two different commercial instruments (Horiba Camsizer⁵⁹ and Malvern MORPHOLOGI G3⁶⁰). In both cases, the programs compute a 2D version of L and W, called L2D and W2D.
The output file structure lists, for each particle, area, perimeter, Xcmax, Xcmin, Fermax, Fermin, W2D, L2D, WM, and LM, where Fermax and Fermin are the maximum and minimum Feret diameters and Xcmax and Xcmin are defined from the chord diameters taken in various directions⁵⁹. It can be shown theoretically that L2D is the same quantity as Xcmax, which can also be seen in the data files. The parameters LM and WM are versions of L2D and W2D defined slightly differently in the Malvern MORPHOLOGI G3 manual⁶⁰. The file format is: Particle name/number, area, perimeter, Fermin, Fermax, Xcmin, Xcmax, W2D, L2D, theta, WM, LM, slo, and nnnF, where nnnF is the number of Fourier coefficients used to represent the particle projection. The quantity theta is the angle, in degrees, that the axis that defines WM and LM makes with the x-axis⁶⁰. The quantity slo is just the ratio of the sine of theta to the cosine of theta. Neither quantities are used in the particle analysis described here and are only included as a check on the computation. The data for each particle comes in sets of three, one line for each of the three projections, (1,2,3) = (L,W,T).

7. Processing 3D and 2D particle geometrical data to produce various graphs

Use any software liked by the user to process the particle size and shape data. Whatever software is used, a certain procedure must be followed.
For the 3D data, combine the SH and nonSH data into SnS and NS lists, using the previously-determined L/T cutoff values for each particle class. Distributions and averages should be computed for the SnS and NS particles separately, and also for the combined SnS and NS data, for all geometrical parameters of interest, such as L, W, T, L/T, W/T, L/W, volume-equivalent spherical diameter, and others.
For the 2D projection data, combine the SH and nonSH data. There are three 2D projections for each 3D particle, taken along the unit vectors for L, W, and T. Combining all three of these projections should give results similar to an experimental technique that randomly rotates the particles before making a projection. Using only the L unit vector data, for instance, simulates an experimental technique in which the particles are roughly aligned along their longest direction, perpendicular to the dropping direction and parallel to the strobe light/projection direction in a typical device.

Representative Results

ASTM has initiated a proficiency testing program (AMPM, Additive Manufacturing Powder Metallurgy) for metal powder used for laser powder bed fusion, where participants carry out a battery of standard metal powder tests and ASTM compiles the statistical distribution of these results in a report to the participants⁶¹. Samples of metal powder are distributed twice per year to all participants. NIST personnel serve as some of the technical advisors to this program, and so have received similar metal powder samples and have analyzed one round of metal powder (AMPM 1810) with the technique described above, which is not yet an ASTM standard.

A total of 16,970 particles were analyzed, of which 14580 were SH particles and 2390 were nonSH particles (see Table 1). A voxel size of 1 µm was used for interior scans of nine fields of view (FOV), with about one thousand 1000 pixel x 1000 pixel images in each FOV. All input and output data files, along with all programs needed to analyze and generate this data, are included in the Supplementary part of this paper at https://doi.org/10.18434/M32265.

Figure 1 shows the two output tiff files for the 500^th slice of one of the microstructures, OriA-0500.tiff, which is the raw gray-scale reconstructed file from the X-ray CT scan, and PixA-0500.tiff has been segmented by a three-phase Otsu⁵⁸ routine that was implemented in pp-Otsu.f.

For these particles, the limiting value of L/T for the SH particles was found to be 1.17 and for the nonSH particles, this limiting value was determined to be 1.10 (see Table 1). For L/T less than these values, the corresponding particles were single near-spherical particles. For L/T larger than these values, the SH and nonSH particles were either double or multiple particles, or single particles that were quite non-spherical. Images will be shown below of some different kinds of particles. This classification scheme was used to separate the particles into two classes: single, near-spherical particles (SnS) and non-spherical (NS) particles.

Table 1 shows other summary results from this characterization. The uncertainties for the L, W, and T measurements were estimated to be about ± 2 µm or two voxel lengths, due to both image segmentation and forcing W and T to be perpendicular to L and each other. Note that most of the particles, 14850 out of 16970 or 87%, were classified as NS, either single and ellipsoidal or otherwise irregular, or else consisting of two or more smaller particles obviously attached together.

Figure 2 shows the particle size distribution, as based on the value of the 3D parameter W, which being between L and T in value is a reasonable choice for a single number to approximately characterize the size of a random particle⁵⁷ but is not always so for strongly non-spherical particles³¹. The y-axis shows the volume fraction of the total amount of particles in a given bin. The area in the bins adds to 1.0. Figure 2A shows the histograms of both the SNS and NS particles graphed separately on the same graph, using the same size bins, and Figure 2b shows all the combined particles, using the same size bins as was used in Figure 2.

Three 2D projections were made for each particle, and the equivalent circular diameter (diameter of circle with equal area to the projected area of a particle, AECD) was used as a measure of particle “size.” Figure 3 shows the area fraction-based histogram of this distribution, for all particles and all projections, with <AECD> = 45 µm.

Figure 4 shows the volume-fraction based distribution of the 3D L/T parameter, using all particles. The long tail in Figure 4 past L/T = 1.3 is mainly composed of particles consisting of two or more particles attached together, with some irregular single particles. By the weight in the histogram in Figure 4, there are obviously a lot of these kinds of particles.

For the 2D projections, we can also define an aspect ratio, AR, as the ratio of the maximum to the minimum Feret diameters and plot its area fraction-based distribution in Figure 5. Note the differences from Figure 4, the 3D L/T aspect ratio, although there is some overall similarity. Differences between 2D and 3D, and the fact that the Feret diameters are not defined the same way as L and T, give rise to the differences between Figure 4 and Figure 5, since exactly the same particles were analyzed. If all the particles were perfect spheres, all the 2D and 3D equivalent graphs would agree perfectly. The average value of AR was <AR> = 1.43.

Some of the particles contain pores, which were detected by the XCT scans and the numerical processing of the segmented images. Table 2 shows a summary of the porosity values in terms of the number of particles having internal pores, the average porosity per particle having pores, and the maximum value of porosity found. The average porosity of about 0.05% might be visualized in the following way: if the average particle was a sphere of diameter 50 µm (see <W> in Table 1) and volume 65,450 µm³, then the pore volume in this particle would be about 33 µm³which, if concentrated in one spherical pore, would have a diameter of about 4 µm. However, at the maximum porosity of 8.6%, this hypothetical single spherical internal pore would have a diameter of about 22 µm, more than a third of the particle diameter.

Figure 6 shows a graph of the porosity of each particle that was porous graphed vs. the diameter of the sphere with the same volume as the given particle (VESD). Figure 6a shows all the particles and Figure 6b cuts off the maximum porosity at 2% to better see the smaller porosity data. There seems to be a slight trend, as seen in Figure 6b, to have higher porosities at smaller particles, which implies that perhaps pore sizes and numbers are similar between particles, so that larger particles, with larger volumes, have lower porosities. Certainly, Figure 6a shows that the highest porosities, more than 2%, are concentrated in the lower size particles.

Figure 1: The 500^th slice from one of the particle microstructures: (a) original gray-scale reconstructed image before segmentation, and (b) after segmentation by a three-phase Otsu routine. Each image is approximately 1 mm in width and height. Please click here to view a larger version of this figure.

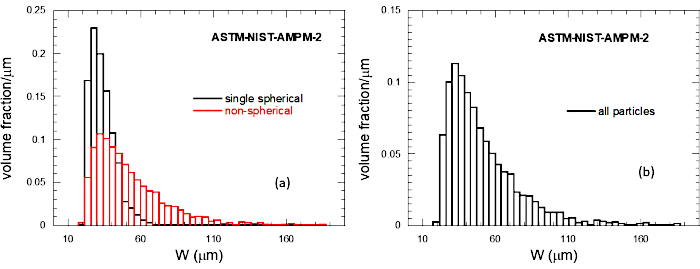
Figure 2: The particle size distribution (PSD) of the particles using W as an approximate measure of the particle size, in µm: (a) SNS and NS PSDs computed separately but displayed on the same graph, and (b) all particles combined. Please click here to view a larger version of this figure.

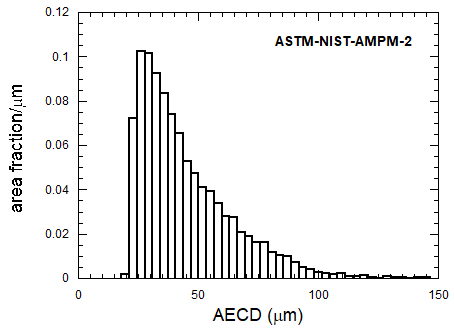
Figure 3: Histogram for the AECD distribution for all particles and 2D projections.

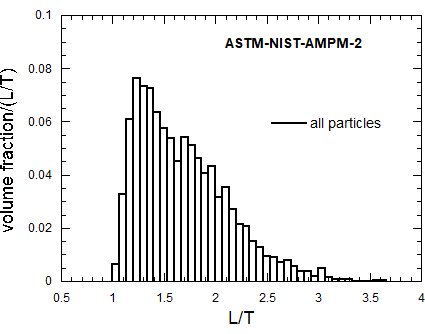
Figure 4: Volume-fraction based L/T histogram for all powder types. Please click here to view a larger version of this figure.

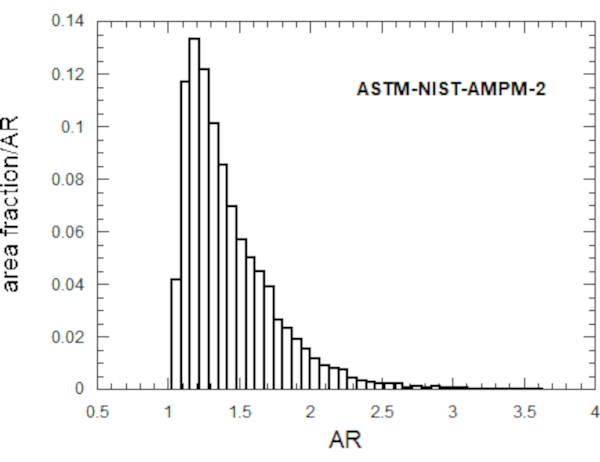
Figure 5: Area fraction-based histogram for the 2D aspect ratio AR, for all particles and projections. Please click here to view a larger version of this figure.

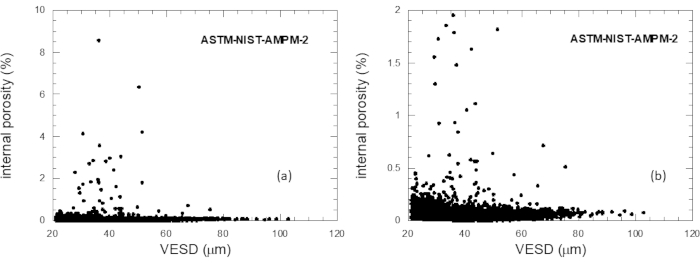
Figure 6: The porosity of each porous particle plotted vs. the VESD of each particle: (a) all porous particles, and (b) just those particles with porosities under 2%. Please click here to view a larger version of this figure.

Particles	#	L/T limit	<L>, µm	<W>, µm	<T>, µm	<L/T>	<W/T>	<L/W>
All	16,970		70	51	41	1.69	1.23	1.37
SH	14580	1.17
nonSH	2390	1.1

SnS	2121		36	34	32	1.12	1.06	1.06
NS	14850		73	52	41	1.73	1.24	1.4

Table 1: Particle numbers, classifications, and dimensional data.

# particles with internal pores	Fraction of particles that had internal pores	Average porosity per porous particle	Maximum porosity found
10074	59%	0.05%	8.60%

Table 2: Internal porosity summary statistics for all particles

Discussion

The XCT-based method for characterizing the 3D size and shape of metal particles has more possible applications but also some limitations. The limitations will be addressed first.

A fast-curing epoxy is used so that the viscosity of the epoxy is high enough to prevent the powder from settling under gravity while the epoxy is curing, or at least reducing the time during which settling could happen and the initial well-spaced dispersion degraded. Some settling can still take place, especially for larger (> 100 µm) size particles. If the volume fraction of the powder is not kept around 10% or less, or if dispersion is not carried out successfully, then in the XCT images there could be some particles that appear to be firmly connected but are really only touching. This can happen as well if there is too much settling of the particles under gravity. If any of these happens, the reconstructed particle XCT images will show this in a clear way and new samples can be made. In the Representative Results presented above, it is possible that a few of the multi-particles were really only artificially touching in the XCT images. However, many random checks have been done on the 3D particle images, for many different metal powders, and this has not been seen.

The method assumes that there will be sufficient X-ray absorption contrast between the particles and the epoxy matrix to make segmentation easy enough to be carried out by an automated method like the Otsu method⁵⁸. This is definitely the case for most metal particles, which usually have densities of 2 g/cm³ or more, with epoxy density being about 1 g/cm³. However, nylon particles are also of interest in the selective laser sintering powder bed process⁶⁴, but they do not have sufficient contrast with epoxy to enable this method to be used. If one could find a different polymer for the matrix, with density significantly less than 1 g/cm³, then this method still might work. Most rock and cements have sufficient density difference from epoxy to allow this method to be effective⁸^,⁹^,¹⁰^,¹¹^,¹²^,¹³^,¹⁴^,¹⁵^,¹⁶^,¹⁷^,¹⁸^,¹⁹^,²⁰^,²¹^,²²^,²³. If a small number of larger particles are to be scanned, polymer foam particles can be mixed in with the particles of interest, without any kind of matrix, to give physical spacing between them that contrasts well with the particles. Small particles, of around 1 mm to 3 mm in size, can be spread out on an adhesive polymer sheet, which is then rolled into a cylindrical sample²¹^,²² for a 3D scan. We also note that if more complex segmentation algorithms are needed for some reason, for instance where there is less contrast of particles with matrix, then they can be used before running pp-Otsu.f, and the particle microstructures can be built using these segmented images. The program will run the three-phase Otsu algorithm on the binary microstructure, but will not change it at all, so the program does not have to be altered.

The part of the Protocol dealing with the XCT scans were for an XCT that can perform interior scans (scans that form virtual cylinders inside the physical sample) of about 1000 pixels wide in the detector used, so that the physical width of the field of view (FOV) is about 1 mm with 1 µm wide voxels. If the XCT instrument used can only do exterior scans (i.e., whole sample scans), then to achieve voxel sizes below 3 µm will require a sample tube smaller than 3 mm in diameter, which will probably be harder to fill and might require a more powerful vacuum pump. The straw would actually have to have an interior diameter of only 1 mm if 1000 pixel by 1000 pixel reconstructed images are used with a voxel size of 1 µm. If the minimum particle size were about 20 µm, as was stated at the beginning of the Protocol, then one could use a 2 µm voxel size with that image size and therefore a 2 mm diameter straw. The criterion of having about 8-10 voxels across the smallest particle in order to have a valid shape analysis also limits the technique to particles that are at least 8 µm to 10 µm in size for 1 µm voxels. Using instruments capable of achieving smaller voxel sizes possible, will extend this technique but with no other changes in the analysis techniques. There is also a soft upper limit on particle size, because fewer larger particles will fit into a sample, so that many more samples and FOVs must be scanned in order to achieve reasonable particle statistics. It was found that various particle geometrical averages, such as L/T, were approximately invariant down to about 250 particles³¹, which is some indication of how many particles must be scanned and analyzed to be able to characterize a particle type/class. However, if 3D voxel information can be obtained on any particle, the same computational techniques can be applied for the shape analysis. With some modifications, these techniques can also be applied to point clouds from a laser scanner¹⁰.

In the Protocol, the segmented particle microstructures were built up from 8bit images. Some XCT instruments have 16bit detectors and can output 16bit reconstructed images. These can be used and separately segmented. But once there are only two colors, white and black, these images should be reduced to 8bit before employing tiff2array.c to build the 3D particle microstructures, since this software is designed to use 8bit images, which are all that are needed for binary images.

We note that the entire 3D particle shape characterization procedure described in this paper is complex, with many steps. In particular, the sample preparation method is somewhat complicated. There has been work with X-ray CT of simple packed powders, from which one could, in principle, acquire the individual particle images required for this particle analysis⁶³. At the expense of having much more complicated 3D image analysis to do in order to separate particles, with probably some artifacts at contact points, one could acquire more particles with one scan with this simpler procedure⁶³. However, one of the main points of the procedure described here is to be able to separate the particles into SnS and NS classes, and for that one must have particles well-separated spatially in the sample that is scanned by the XCT.

The final step in the method, in order to be able to separate the metal powder into SnS and NS particles, requires a visual inspection of a random subset of the particles. But even though this random subset is 100 SH and 100 nonSH particles, 10 in each 0.1 range of L/T between 1 and 2, ordering them by L/T and starting the visual inspection from the smallest L/T value only requires about 20 particles of each type to be examined, as cutoff/T values are usually around 1.2. It is possible that some form of machine learning could be developed for determining these L/T cutoffs⁶⁴^,⁶⁵.

Generating the 2D projection files enables the computation of many 2D shape quantities. For convex particles, it is fairly simple to describe the mathematical relationship between these, and in fact, for convex particles, many of the size parameters computed in these programs are equal. For star-shape particles, or nonSH and non-convex particles, it is not clear how these proofs would be made and in fact these quantities may differ slightly from each other.

These are two other important applications of this technique that should be mentioned here. The first is that if some solid sample, not a powder sample, contains discrete pores, then the pores can be treated as particles and the method used to study their shape, size, and orientation in 3D⁵⁹. Many commercial image analysis packages also can do this, but not with the spherical harmonic fitting algorithm. Usually an ellipsoid is fit to each separate pore to extract shape, size, and orientation. The second application is to a powder, such as a sand or crushed rock, where no true multi-particles are really possible, because of a lack of chemical/physical mechanisms that might bond particles together, and because of physical mechanism like crushing that would break apart such particles made out of a brittle material. But even in this case, there can still be artificially touching particles after the reconstruction step, especially if too high a concentration of particles was used in the epoxy-embedded powder samples or if the particles are very elongated or disc-like or settling occurred, so that particles can nearly touch even at a low volume fraction⁵⁴. The L/T cutoff analysis can be used to eliminate all such artificially touching particles from the particle analysis.

Disclosures

The authors have nothing to disclose.

Acknowledgements

The authors would like to acknowledge the long-term support of NIST for 3D powder analysis.

Materials

Epoxy

Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/

Hardman Part # 4001

case of 100

References

Allen, T. . Powder Sampling and Particle Size Determination, 1st edition. , (2003).
Rodriguez, J., Edeskär, T., Knutsson, S. Particle shape quantities and measurement techniques: a review. Electron Journal of Geotechnical Engineering. , 18 (2013).
Garboczi, E. J., Douglas, J. F. Intrinsic conductivity of objects having arbitrary shape and conductivity. Physical Review E. 53, 6169-6180 (1996).
Mansfield, M. L., Douglas, J. F., Garboczi, E. J. Intrinsic viscosity and the electrical polarizability of arbitrarily shaped objects. Physical Review E. 64, 61401-61416 (2001).
Garboczi, E. J., Douglas, J. F., Bohn, R. B. A hybrid finite element-analytical method for determining the intrinsic elastic moduli of particles having moderately extended shapes and a wide range of elastic properties. Mechanics of Materials. 38, 786-800 (2006).
Garboczi, E. J., Douglas, J. F. Elastic Moduli of Composites Containing a Low Concentration of Complex-Shaped Particles Having a General Property Contrast with the Matrix. Mechanics of Materials. 5, 53-65 (2012).
Audus, D. J., Hassan, A. M., Garboczi, E. J., Hudson, S. D., Douglas, J. F. Interplay of particle shape and suspension properties: A study of cube-like particles. Soft Matter. 11, 3360-3366 (2015).
Garboczi, E. J., Bullard, J. W. Shape analysis of a reference cement. Cement and Concrete Research. 34, 1933-1937 (2004).
Masad, E., Saadeh, S., Al-Rousan, T., Garboczi, E. J., Little, D. Computations of particle surface characteristics using optical and x-ray CT images. Computational Materials Science. 34, 406-424 (2005).
Cheok, G. S., Stone, W. C., Garboczi, E. J. Using LADAR to characterize the 3-D shape of aggregates: Preliminary results. Cement and Concrete Research. 36, 1072-1075 (2006).
Mahmoud, E., Gates, L., Masad, E., Garboczi, E. J. Comprehensive Evaluation of AIMS Texture, Angularity, and Dimensions Measurements. Journal of Materials in Civil Engineering. 22, 369-379 (2010).
Erdoğan, S. T., Nie, X., Stutzman, P. E., Garboczi, E. J. Micrometer-scale 3-D imaging of eight cements: Particle shape, cement chemistry, and the effect of particle shape on laser diffraction size analysis. Cement and Concrete Research. 40, 731-739 (2010).
Holzer, L., Flatt, R., Erdoğan, S. T., Nie, X., Garboczi, E. J. Shape comparison between 0.4 µm to 2.0 µm and 20 µm to 60 µm cement particles. Journal of the American Ceramic Society. 93, 1626-1633 (2010).
Erdoğan, S. T., Fowler, D. W., Garboczi, E. J. Shape and size of microfine aggregates: X-ray microcomputed tomography vs. laser diffraction. Powder Technology. 177, 53-63 (2007).
Garboczi, E. J., Liu, X., Taylor, M. A. The Shape of a Blasted and Crushed Rock Material over More than Three Orders of Magnitude: 20 µm to 60 mm. Powder Technology. 229, 84-89 (2012).
Cepuritis, R., Wigum, B. J., Garboczi, E. J., Mørtsell, E., Jacobsen, S. Filler from crushed aggregate for concrete: Pore structure, specific surface, particle shape and size distribution. Cement and Concrete Composites. 54, 2-16 (2014).
Cepuritis, R., Garboczi, E. J., Jacobsen, S., Snyder, K. A. Comparison of 2-D and 3-D shape analysis of concrete aggregate fines from VSI crushing. Powder Technology. 309, 110-125 (2017).
Cepuritis, R., Garboczi, E. J., Jacobsen, S. Three-dimensional shape analysis of concrete aggregate fines produced by VSI crushing. Powder Technology. 308, 410-421 (2017).
Cepuritis, R., Garboczi, E. J., Ferraris, C. F., Jacobsen, S., Sørensen, B. E. Measurement of particle size distribution and specific surface area for crushed concrete aggregate fines. Advanced Powder Technology. 28, 7065 (2017).
Erdogan, S. T., Forster, A. M., Stutzman, P. E., Garboczi, E. J. Particle-based characterization of Ottawa sand: Shape, size, mineralogy, and elastic moduli. Cement and Concrete Composites. 83, 36-44 (2017).
Olivas, A., et al. Certification of SRM 2493: Standard Reference Mortar for Rheological Measurements. NIST Special Publication. , 260 (2017).
Martys, N., Peltz, W., George, W., Toman, B., Garboczi, E. J. . Certification of SRM 2497: Standard Reference Concrete for Rheological Measurement, NIST SP1237. , (2019).
Estephane, P., Garboczi, E. J., Bullard, J. W., Wallevik, O. H. Three-dimensional shape characterization of fine sands and the influence of particle shape on the packing and workability of mortars. Cement and Concrete Composites. 97, 125-142 (2019).
Slotwinski, J. A., et al. Characterization of Metal Powders Used for Additive Manufacturing. Journal of Research of the National Institute of Standards and Technology. 119, (2014).
Grell, W. A., et al. Effect of powder oxidation on the impact toughness of electron beam melting Ti-6Al-4V. Additive Manufacturing. 17, 123-134 (2017).
Garboczi, E. J., Hrabe, N. Particle shape and size analysis for metal powders used for additive manufacturing: Technique description and application to a gas-atomized Ti64 powder and a plasma-atomized Ti64 powder. Additive Manufacturing. 31, 100965 (2020).
Garboczi, E. J. Three-Dimensional Shape Analysis of JSC-1A Simulated Lunar Regolith Particles. Powder Technology. 207, 96-103 (2011).
Chiaramonti, A. N., Goguen, J. D., Garboczi, E. J. Quantifying the 3-Dimensional Shape of Lunar Regolith Particles Using X-Ray Computed Tomography and Scanning Electron Microscopy at Sub-λ Resolution. Microscopy and Microanalysis. 23, (2017).
Escobar-Cerezo, J., et al. An Experimental Scattering Matrix for Lunar Regolith Simulant JSC-1A at Visible Wavelengths. The Astrophysical Journal Supplement Series. 235, 19 (2018).
Hu, M., Zhang, T., Stansbury, J., Neal, J., Garboczi, E. J. Determination of Porosity and Thickness of Biofilm Attached on Irregular-Shaped Media. Journal of Environmental Engineering. 139 (7), 923-931 (2013).
Garboczi, E. J., Riding, K. A., Mirzahosseini, M. Particle shape effects on particle size measurement for crushed waste glass. Advanced Powder Technology. 28, 648-657 (2017).
Baidya, S., et al. Analysis of Different Computational Techniques for Calculating the Polarizability Tensors of Stem Cells with Realistic Three-Dimensional Morphologies. IEEE Transactions on Biomedical Engineering. , (2018).
Vargas-Lara, F., Hassan, A. M., Garboczi, E. J., Douglas, J. F. Intrinsic Conductivity of Carbon Nanotubes and Graphene Sheets Having a Realistic Geometry. Journal of Chemical Physics. 143, 204902 (2015).
Hassan, A. M., Vargas-Lara, F., Douglas, J. F., Garboczi, E. J. Electromagnetic Resonances of Individual Single-Walled Carbon Nanotubes with Realistic Shapes: A Characteristic Modes Approach. IEEE Transactions on Antennas and Propagation. 64, 2743 (2016).
Durbhakula, K. C., et al. Electromagnetic Scattering From Individual Crumpled Graphene Flakes: A Characteristic Modes Approach. IEEE Transactions on Antennas and Propagation. 65, 6035 (2017).
Hassan, A. M., et al. Electromagnetic Scattering from Multiple Single-Walled Carbon Nanotubes Having Tumbleweed Configurations. IEEE Transactions on Antennas and Propagation. 65, (2017).
Malavé, V., Killgore, J. P., Garboczi, E. J., Berger, J. R. Decoupling the effects of surface topography and material heterogeneity on indentation modulus: A simple numerical linear-elastic model. International Journal of Solids and Structures. 124, 235-243 (2017).
Garboczi, E. J. The influence of particle shape on the results of the electrical sensing zone method as explained by the particle intrinsic conductivity. Powder Technology. 322, 32-40 (2017).
Garboczi, E. J. Three-dimensional mathematical analysis of particle shape using x-ray tomography and spherical harmonics: Application to aggregates used in concrete. Cement and Concrete Research. 32, 1621-1638 (2002).
Erdoğan, S. T., et al. Three-dimensional shape analysis of coarse aggregates: New techniques for and preliminary results on several different coarse aggregates and reference rocks. Cement and Concrete Research. 36, 1619-1627 (2006).
Taylor, M. A., Garboczi, E. J., Erdoğan, S. T., Fowler, D. W. Some properties of irregular particles in 3-D. Powder Technology. 162, 1-15 (2006).
Garboczi, E. J., Bullard, J. W. Contact function, uniform-thickness shell volume, and convexity measure for 3D star-shaped random particles. Powder Technology. 237, 191-201 (2013).
Bullard, J. W., Garboczi, E. J. Defining shape measures for 3D star-shaped particles: Sphericity, roundness, and dimensions. Powder Technology. 249, 241-252 (2013).
Jia, X., Garboczi, E. J. Advances in shape measurement in the digital world. Particuology. 26, 19-31 (2016).
Garboczi, E. J., Bullard, J. W. 3D analytical mathematical models of random star-shape particles via a combination of X-ray computed microtomography and spherical harmonic analysis. Advanced Powder Technology. 28, 325-339 (2017).
Qian, Z., Garboczi, E. J., Ye, G., Schlangen, E. Anm: A geometrical model for the composite structure of mortar and concrete using real-shape particles. Materials and Structures. 49 (1), 149-158 (2015).
Thomas, S., Lu, Y., Garboczi, E. J. Improved model for 3-D virtual concrete: Anm model. Journal of Computing in Civil Engineering. , (2015).
Zuo, Y., Qian, Z., Garboczi, E. J., Ye, G. Numerical simulation of the initial particle parking structure of cement/geopolymer paste and the dissolution of amorphous silica using real-shape particles. Construction and Building Materials. 185, 206-219 (2018).
Lu, Y., Islam, A., Thomas, S., Garboczi, E. J. Three-dimensional mortar models using real-shaped sand particles and uniform thickness interfacial transition zones: Artifacts seen in 2D slices. Construction and Building Materials. 236, 117590 (2020).
Grigoriu, M., Garboczi, E. J., Kafali, C. Spherical harmonic-based random fields for aggregates used in concrete. Powder Technology. 166, 123-138 (2006).
Liu, X., Garboczi, E. J., Grigoriu, M., Lu, Y., Erdoğan, S. T. Spherical harmonic-based random fields based on real particle 3D data: Improved numerical algorithm and quantitative comparison to real particles. Powder Technology. 207, 78-86 (2011).
Stauffer, D., Aharony, A. . Introduction To Percolation Theory: Revised, second edition. , (1994).
Bentz, D. P., Garboczi, E. J. Percolation of phases in a three-dimensional cement paste microstructural model. Cement and Concrete Research. 21, 325-344 (1991).
Garboczi, E. J., Snyder, K. A., Douglas, J. F., Thorpe, M. F. Geometrical percolation threshold of overlapping ellipsoids. Physical Review E. 52, 819-828 (1995).
Garboczi, E. J., Bentz, D. P., Stauffer, D. Computer simulation and percolation theory applied to concrete, in. Annual Reviews of Computational Physics VII. , 85-123 (2000).
Garboczi, E. J. Percolation phase diagrams for multi-phase models built on the overlapping sphere model. Physica A: Statistical Mechanics and its Applications. 442, 156-168 (2016).
Fernlund, J. M. R. The effect of particle form on sieve analysis: a test by image analysis. Engineering Geology. 50 (1), 111-124 (1998).
Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Transactions on Systems, Man, and Cybernetics. 9, 62-66 (1979).
. Horiba Available from: https://www.horiba.com/fileadmin/uploads/Scientific/Documents/PSA/Manuals/CAMSIZER_Characteristics_Nov2009.pdf (2020)
. Malvern MORPHOLOGI G3 Available from: https://www.malvernpanalytical.com/en/support/product-support/morphologi-range/morphologi-g3 (2020)
. ASTM Available from: https://www.astm.org/STATQA/Additive_Manufacturinng_Powder_Metallurgy.htm (2020)
Bain, E., Garboczi, E. J., Seppala, J., Parker, T., Migler, K. AMB2018-04: Benchmark Physical Property Measurements for Powder Bed Fusion Additive Manufacturing of Polyamide 12. Integrating Materials and Manufacturing Innovation. , (2019).
du Plessis, A., Sperling, P., Beerlink, A., du Preez, W., le Roux, S. G. Standard method for microCT-based additive manufacturing quality control 4: Metal powder analysis. MethodsX. 5, 1336-1345 (2018).
DeCost, B. L., Jain, J., Rollett, A. D., Holm, E. A. Computer vision and machine learning for autonomous characterization for AM powder feedstocks. JOM. 69, 456-465 (2017).
DeCost, B. L., Holm, E. A. Characterizing powder materials using keypoint-based computer vision methods. Computational Materials Science. 126, 438-445 (2017).

Automatically Generated