Quantitative Hardness Measurement by Instrumented AFM-indentation
Summary
This experimental protocol describes how atomic force microscopy can be used to measure hardness at the true nanometer scale and to detect single atomistic plasticity events.
Abstract
In this work, a combination of amplitude-modulated non-contact atomic force microscopy and atomic force spectroscopy is applied for instrumented hardness measurements on an Au(111) surface with atomistic resolution of single plasticity events. A careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. A typical curve displays a clear elastic deformation regime up to the first plasticity event, or pop-in, with a length in the range of one to two Burger’s vectors. Later plasticity events exhibit the same magnitude. The work of plasticity is further extracted from the measurements. Finally, the hardness is determined in combination with the indentation curve using non-contact atomic force microscopy images of the remaining indents.
Introduction
For the last 150 years, hardness values have been used to characterize the mechanical behavior of materials and to predict their performance under various loading conditions. The hardness of a material describes the resistance of its surface to the penetration of a harder indenter. For metallic materials, the hardness relates to resistance to plastic flow.
Although the implementation of hardness testing has proven to be relatively easy, the yielded results have long been rather empirical, making them unable to describe the intrinsic properties of the investigated material. The empirical nature of hardness testing results has been a consequence of the use of various indenter geometries, each of which has a different established hardness scale. However, all empirical hardness scales, such as the Brinell hardness (HB) test for spherical indenters and the Vickers (HV) and Knoop (HK) hardness tests for different types of four-sided pyramids, have one thing in common: the hardness number is determined from the ratio of the applied load to the developed area of the remaining indent. In an attempt to relate the hardness of metals to their fundamental mechanical properties, the hardness measured with a spherical indenter has been defined as the ratio of the applied load to the projected area of the remaining indent. This hardness value, also known as the Meyer’s hardness (H), is equal to the mean contact pressure and directly relates to the yield strength of non-work-hardening metals1.
Hardness testing has long been limited to the macro-scale, in which case the sizes of indents have been measured by optical means. The development of instrumented indentation, where force-displacement curves are recorded, has been recognized as a valuable alternative for determining the hardness of a material, although the size of the remaining indent may be too small to be accurately imaged. In this case, the projected area of the indent is calculated from the tip displacement according to a so-called indenter-area function2. Due to this development, the analysis of the curvature of force-displacement curves and of the occurrence of distinct plasticity events in the shape of pop-ins is now widely used to study the mechanisms of plastic deformation at the micrometer scale, such as by means of nanoindentation3.
It is well accepted that the carriers of plastic deformation in metals, i.e., dislocations, operate at the nanometer scale. To understand their modes of operation at the atomic level, new experimental techniques with atomic resolution are needed. Initial investigations of atomistic plasticity events at the interfaces between nanometer-sized single asperities and single crystalline Au surfaces of different orientations have been carried out by interfacial force microscopy (IFM)4, 5. Atomic force microscopy (AFM) indentation has been applied to observe the nucleation and gliding of single dislocations in KBr(100) single crystals6, Cu(100)7, and Au(111)8, 9. There, atomistic plasticity events were observed in the shape of pop-ins, with lengths in the range of 1 Å. AFM indentation has also been used to measure the nano-hardness and -elasticity of gold nano-island grown on mica10. In this work, the nano-hardness was found to be smaller than the bulk value and was observed to depend linearly on the indentation area. Also, a detailed measurement protocol has been proposed to determine the hardness of hard surfaces, such as fused quartz and silicon, by AFM indentation with a diamond-tipped sapphire cantilever11. In particular, this method takes into account the non-linearity of the photo-sensitive deflection detectors for large cantilever deflection12. More recently, AFM indentation and non-contact AFM imaging have been combined to quantitatively determine the hardness and the fundamental mechanisms of plastic deformation of a Pt(111) single crystalline surface and Pt-based metallic glass13. For Pt(111), plastic deformation mechanisms at the nanometer scale were found to be consistent with the discrete mechanisms established for larger scales. Further, the nanometer-scale plastic deformation of the metallic glass was found to be not discrete, but rather continuous and highly localized around the indenting tip. These results revealed a lower size limit for metallic glasses, below which shear transformation mechanisms are not activated by indentation. AFM indentation has also been used to determine the hardness values of biological samples (such as collagen fibrils)14, polymers15, and colloidal crystals16.
In the present work, a careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. Further representative results are shown and discussed in the light of recent findings in the field of plastic deformation of small volumes.
For this experiment, an atomic force microscope (AFM) was used. The cornerstone of an AFM is its micro-fabricated force sensor (usually a cantilever beam), with a sharp tip at the end whose radius is in the range of several nanometers. In the particular configuration of the instrument used for this experiment, the cantilever is mounted onto a piezo-electric z-scanner, while the sample to be investigated is mounted onto a piezo-electric x/y-scanner. During AFM imaging, the force sensor tip is scanned over a sample to register interaction forces with the sample surface that result in a deflection of the cantilever according to Hooke’s law. The static or dynamic deflection of the cantilever can be measured with an optical beam deflection detector, consisting of a laser diode, a set of mirrors, and a photodiode that converts the cantilever deflection into a voltage. During imaging, the signal at the photodiode is controlled by a feedback loop so as to keep the interaction forces at the sample surface; this results in adjustments of the z-scanner position, which are recorded and displayed as a topography image.
Prerequisites for the experiment described below are that the piezo-electric scanners of the atomic force microscope are well-calibrated and that the instrument stays in the laboratory at a constant temperature and humidity level. The reader should be aware that, depending on the atomic force microscope model, some of the experimental procedure steps may have to be modified. In particular, all measurements are performed after setting the scanners’ ranges to “small”; this function allows for the reduction of the x/y-scanner range to 5 x 5 µm² and the z-scanner range to 4 µm, which ensures a resolution at small scales. This function is not available on all commercial AFM and is not mentioned in the remainder of the text.
For data analysis, the use of the free SPM data analysis software Gwyddion17 and the Matlab software package18 are recommended.
This protocol gives a description of the experimental procedure to be followed in order to perform instrumented hardness measurements by AFM. Since the handling of different commercial AFMs may differ from one model to the other, the reader should refer to the manual provided by the AFM manufacturer for detailed setting procedures and software information. In the following text, in order to reproduce the described experiment, it is assumed that the reader is familiar with the handling of the particular AFM used here.
Protocol
1. Instrumental Set-up and Calibration
- Instrumental set-up
- Use a stiff diamond-coated cantilever of the type DT-NCLR or CDT-NCLR with a first free resonance frequency f0,1 ≥ 180 kHz, a quality factor Q ≥ 300, and a bending stiffness k ≥ 40 N/m.
- Mount the selected cantilever onto a clamping holder provided by the AFM manufacturer. Take special care to place the cantilever such that its long axis is perpendicular to the fast scan direction of the AFM. Alternatively, glue the cantilever onto a cantilever holder provided by the AFM manufacturer using dual-component epoxy glue.
- Mount the cantilever holder onto the AFM head and use the optical microscope normally available with the AFM system to focus on the AFM cantilever. Double check that the cantilever's long axis is perpendicular to the fast scan direction. If not, go back to Section 1.1.2.
- Align the laser beam so that it is reflected at the end of the cantilever. Monitor the voltage sum at the photodiode and conduct a fine adjustment to maximize the sum signal. Typical sum signal values are in the range of 2 V.
- Adjust the mirror's horizontal and vertical tilt angles so as to bring the reflected laser spot into the center of the photodiode, where the voltages corresponding to the vertical and lateral displacement are nearly zero.
- Calibration
- Perform a frequency sweep to determine the first free bending resonance f0,1 of the cantilever.
- Determine the bending stiffness of the cantilever k, calculated according to19
(1)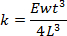
where E is the Young's modulus, L is the length of the cantilever, w is the width of the cantilever, and t is its thickness. To this end, measure the length and width of the cantilever by optical microscopy or scanning electron microscopy for better accuracy. Calculate the thickness of the cantilever from its first free bending resonance frequency f0,1, according to
(2)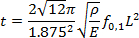
where ρ is the mass density. - Select the default value of the photodiode sensitivity for the particular cantilever type to be used for the experiment in the set up menu of the AFM. Bring the cantilever tip into contact with the reference sample at a load Fn = 10 nN by clicking the approach button.
- Open the force spectroscopy menu in the AFM software and set the relative retraction and extension of the z-scanner to 50 nm and the z-scanner retraction/extension to 0.3 µm/sec. Doing so, the recording of the force-distance curve will consist first of a retraction of the z-scanner to 50 nm away from the sample surface and then of a series of approaches and retractions of the same distance.
- Record a force distance curve with the set parameters suggested in 1.2.4 on a smooth and non-compliant surface, such as nano-crystalline diamond or sapphire, in order to avoid sample deformation effects. To do so click on the acquire button in the force spectroscopy menu of the AFM software.
- Fit the repulsive part of the force-distance curve with a linear function, in the calibration menu of the AFM software. The inverse slope of the fitting line corresponds to the photodiode sensitivity S. Substitute the determined value to the default value of the instrument software in the calibration menu of the AFM software by clicking the execute calibration button.
2. Sample Preparation
NOTE: The sample measured in this experiment consists of a 100-nm-thick, atomically smooth Au(111) thin film grown on mica by physical vapor deposition.
- Mount the sample onto a magnetic sample holder provided by the instrument manufacturer by means of double-sided carbon tape. In order to avoid drift of the sample during measurements, mount the sample one day before the measurements, so as to let the carbon tape relax. Alternatively, mount the sample onto the holder with silver paint, which usually dries within a few minutes.
- Mount the magnetic sample holder onto the x/y scanner.
3. Measurement Procedure
- Set the oscillation frequency slightly off-resonance (in this experiment f = 190.67 kHz) and the oscillation amplitude at A = 20 nm Note that these values are automatically set by the instrument software for this particular cantilever. Set the oscillation set point manually at Aset-point = 5 nm.
- Draw the cantilever toward the sample surface using the step-motor of the AFM. Make sure that the force sensor does not collide with the sample surface. Keep the cantilever in focus during coarse approach and stop the coarse approach before the sample surface is in perfect focus.
- Automatically approach the force sensor by clicking on the approach button. Once the oscillation amplitude has reached its set point, the tip is ready to scan the topography of the sample surface.
- Record a series of topography images on areas ranging from 5 x 5 to 1 x 1 µm² (if available, adjust the slope of the topography signal by tilting the x/y-scanner). Make sure that successive images of the same area do not exhibit any sign of drift and that the z-scanner position remains almost constant. If this is not the case, continue imaging until the system has stabilized.
- Once the system has stabilized and a smooth 1 x 1 µm² area has been found, retract the force sensor a few micrometers from the sample surface by clicking on the retract button.
- Select the force spectroscopy mode in the instrument menu and move the force sensor to the middle of the preselected 1 x 1 µm² area, with a force set-point of 10 nm. Monitor the position of the z-scanner until it remains constant.
- Select the 2 x 2 grid of points whose center corresponds to the center of the preselected 1 x 1 µm² area. Set the distance between two next neighboring points at 500 nm.
- Set the relative scanner distance to vary from 0 to 150 nm at a speed of 300 nm/sec and to then retract over the same distance and at the same velocity. Given the tilt angle of the cantilever with regard to the sample surface, apply a tilt correction by moving the lateral scanner by Z × tanφ during a vertical scanner extension Z, where φ is the tilt angle20.
NOTE: A few instruments account for the cantilever tilt in their force spectroscopy or indentation mode; this is the case for the AFM used in this work. - Press the start button in the instrument software to begin the acquisition of the AFM indentation data.
- Once the AFM indentation measurements have been completed, retract the force sensor a few micrometers away from the sample surface.
- Select the non-contact AFM mode imaging in the instrument software menu and repeat the procedure described in Sections 3.1 and 3.2.
- Perform a scan over the same 1 x 1 µm² surface area as in Section 3.3 so as to locate the exact position of the indents. Further surface scans over a 500 x 500 nm² surface area can be performed to image the remaining indents with greater detail.
4. Data Analysis
- Image processing
- Process the recorded topography images so as to align the lines in the fast scan direction based on median difference. Use the built-in function of Gwyddion.
- Calculate the projected area Ap of indents using the indentation analysis function of Gwyddion.
- Estimate the AFM tip shape from the topography images of indents by using the tip analysis function of Gwyddion. Then average the tip shape images and measure the half-opening angle α of the averaged tip shape.
- Convert the force-distance curves into force-displacement curves by calculating the tip displacement δ according to13
(3)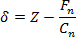
where Z is the relative scanner position. - Now, plot the force versus the tip displacement. The resulting curve usually displays so-called pop-ins, with lengths in the range of several 100 pm, that correspond to atomistic plasticity events. Use the first of these pop-ins to determine the tip displacement at the elastic limit δel4.
- Fit the elastic part of the force-displacement curve with the Hertzian function21.
(4)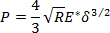
where R is the tip radius and E'* is the reduced modulus of elasticity, given by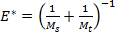 , with Ms,t being the indentation modulus of the sample and of the tip, respectively. In this case, the fit parameter is
, with Ms,t being the indentation modulus of the sample and of the tip, respectively. In this case, the fit parameter is 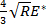 .
. - Extend the fit function into the plasticity regime so as to calculate the work of plasticity Wplasticity from the areal difference between the fit function and the experimental curve21.
- Calculate the hardness of the sample according to1, 2
(5)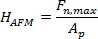
and
(6)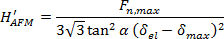
where Fn,max is the maximal applied load, Ap is the projected area of the indent calculated in Section 4.2, α is the half-opening angle of the tip calculated in Section 4.3, δel is the tip displacement at the first plasticity event, and δmax is the maximal tip displacement (See Section 4.4).
Representative Results
In this work, the bending stiffness of the cantilever k was calculated according to the geometrical beam theory19. For the particular diamond-coated cantilever used in this work, we found k = 55.69 N/m. Note that we neglected the diamond coating; the thickness of the diamond coating is one to two orders of magnitude smaller than the cantilever thickness and thus does not significantly increase its bending stiffness (although its Young's modulus is significantly larger than that of silicon).
In order to avoid sample deformation effects, the sensitivity of the photodiode was determined by recording the force-distance curve with the previously-calibrated force sensor on a smooth nano-crystalline diamond surface with a Young's modulus E = 759 GPa22. The force signal was recorded in volt units (the unit of the photodiode signal) and over a small range of repulsive forces in order to avoid tip deformation and damage. The repulsive part of the force-distance curve was then fitted with a linear function, the inverse slope of which corresponds to the photodiode sensitivity S. In this particular experiment, the sensitivity of the photodiode was determined to be S = 23.903 nm/V. The assumption of a linear response of the photodiode is limited to when the base displacement of the cantilever is smaller than 500 nm. For larger displacements Z, the non-linearity of the photo-sensitive detector needs to be considered, in which case the Z-VPD response is a third-order polynomial12. For the calibration, the base displacement was set to 50 nm, while in our experiments, the base displacement was 150 nm. In these cases, we considered the response of the photodiode to be linear.

Figure 1: Surface topography of a gold thin-film surface. (Left) Non-contact AFM topography image of a 5 x 5 µm2 and (right) of a 1.25 x 1.25 µm2 Au thin-film surface area displaying micrometer-sized grains, each of which exhibits an atomically flat Au(111) surface consisting of large terraces and monoatomic steps. Please click here to view a larger version of this figure.
Figure 1 shows non-contact AFM topography images of a gold thin-film surface. The thin-film surface is found to consist of grains in the micrometer range. Each grain exhibits an atomically flat Au(111) surface consisting of large terraces and monoatomic steps. Figure 2 shows the indents caused during indentation measurements by an AFM tip with a maximal vertical force of 7.2 µN applied on the same Au(111) thin-film surface as in Figure 1. Also, the topography difference between the imaged area before and after a series of four indentations at distinct locations is displayed in Figure 2(c). It is worth noting how similar all remaining indents look. This similarity attests to the stability of the tip and the reproducibility of the measurements.
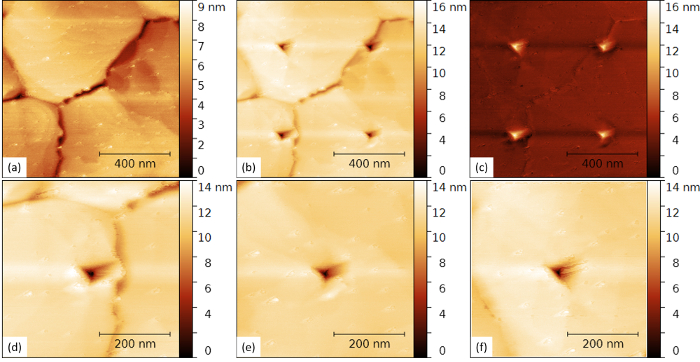
Figure 2: AFM indents on an atomically smooth gold thin-film surface. (a) Non-contact AFM topography image of a 1 x 1 µm2 Au thin-film surface area selected for AFM indentation measurements. (b) Non-contact AFM topography image of the same surface area in (a) after four consecutive AFM indentation measurements up to a vertical force Fn = 7.2 μN. (c) Topography difference between images in (a) and (b). (d – f) Non-contact AFM topography images of three individual AFM indents shown in (b). Please click here to view a larger version of this figure.
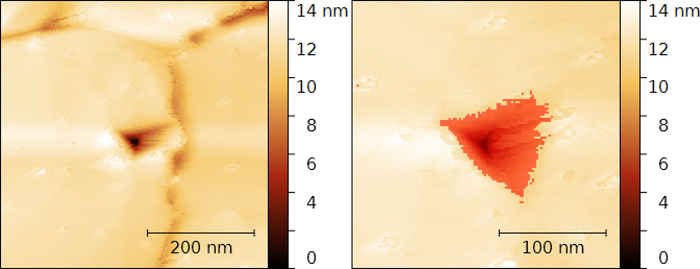
Figure 3: Calculation of the projected area of an AFM indent on an atomically smooth gold thin-film surface. (Left) Non-contact AFM topography images of individual AFM indents shown in Figure 2. (Right) Same topography image as in the left panel after cropping and with an overlaid mask used to calculate the projected area using the free SPM data analysis software Gwyddion. The projected area is found to be Ap = 4703.52 nm2; this yields a hardness value HAFM = 1.53 GPa. Please click here to view a larger version of this figure.
Figure 3 demonstrates the procedure to determine the projected area of an indent by masking the area with negative topography values relative to the unmarred surface. From this measurement, the projected area of the indent is found to be Ap = 4703.52 nm². The indentation was performed with a maximal load Fn,max = 7.2 µN (see Figure 4). Accordingly, the hardness can be calculated as 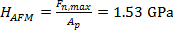 . The measured Ap-value is likely to be underestimated by tip convolution effects during imaging, on the one hand, and by elastic recovery effects upon unloading23, on the other.
. The measured Ap-value is likely to be underestimated by tip convolution effects during imaging, on the one hand, and by elastic recovery effects upon unloading23, on the other.
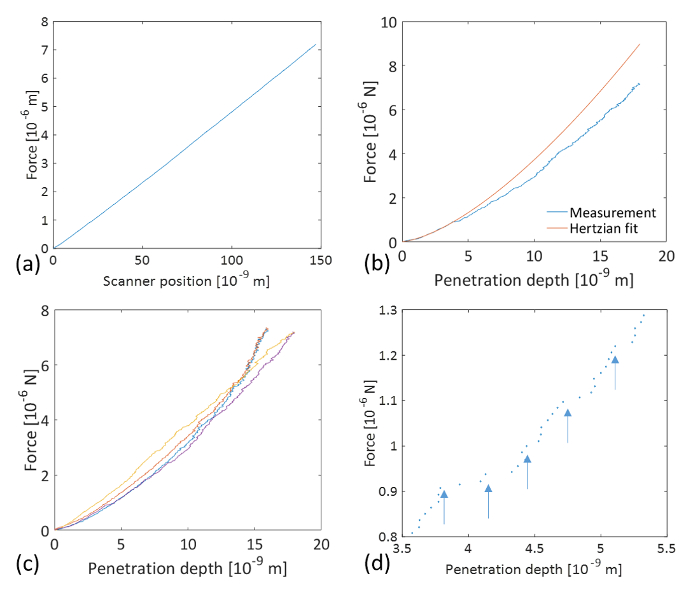
Figure 4: Indentation curves from force-distance curves measured by AFM. (a) Typical loading part of a force-distance curve measured by AFM on an atomically smooth Au thin-film surface. (b) Force-displacement curve calculated according to Equation (3) (blue line) and the Hertzian fit (red line) of the elastic part up to the first observable plasticity event (pop-in) at Fn = 0.908 µN, with tip displacement δel = 3.786 nm (the length of the first pop-in is measured to be λpop-in = 543 pm) according to Equation (4). The corresponding fit parameter is determined to be 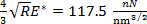 , where R is the indenter radius and E* is the reduced modulus of elasticity. Note that the Hertzian fit curve is extended beyond the elastic regime so as to calculate the work of plasticity Wplasticity from the integrated difference between the Hertzian fitting curve and the experimental result; Wplasticity = 11.44 x 10-15 J. (c) Series of four consecutive force-penetration curves. (d) Magnified view of the force-penetration curve shown in (b) showing pop-ins with lengths in the range of several 100 pm (indicated by arrows). Please click here to view a larger version of this figure.
, where R is the indenter radius and E* is the reduced modulus of elasticity. Note that the Hertzian fit curve is extended beyond the elastic regime so as to calculate the work of plasticity Wplasticity from the integrated difference between the Hertzian fitting curve and the experimental result; Wplasticity = 11.44 x 10-15 J. (c) Series of four consecutive force-penetration curves. (d) Magnified view of the force-penetration curve shown in (b) showing pop-ins with lengths in the range of several 100 pm (indicated by arrows). Please click here to view a larger version of this figure.
Figure 4 shows indentation curves calculated from force-distance curves measured by AFM. It is important to note how the curves overlap, which further attests to the reproducibility of the measurements. In Figure 4(b), a force-displacement curve calculated from a force-distance curve (Figure 4(a)) according to Equation (3) is fitted with the Hertzian fit (Equation (4)) over its elastic part. The elastic limit was determined from the first observable plasticity event (pop-in) at Fn,el = 0.908 µN and at the tip displacement δel = 3.786 nm (the length of the first pop-in is measured to be λpop-in = 543 pm). The corresponding fit parameter is determined to be 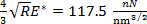 , where R is the indenter radius and E* is the reduced modulus of elasticity. While it may be tempting to extract the indentation modulus of gold MAu(111) from the fitting parameter, the radius at the tip apex and the indentation modulus of the diamond-coated tip remain uncertain. In principle, the indenter properties can be calibrated by indenting on a calibration sample. The determination of the indentation modulus of Au(111) is beyond the scope of this work. Assuming an elasticity modulus for Au(111) EAu = 80 GPa, a Poisson's ratio νAu = 0.45, and a tip Enc-diamond = 759 GPa and νnc-diamond = 0.003, we calculate from
, where R is the indenter radius and E* is the reduced modulus of elasticity. While it may be tempting to extract the indentation modulus of gold MAu(111) from the fitting parameter, the radius at the tip apex and the indentation modulus of the diamond-coated tip remain uncertain. In principle, the indenter properties can be calibrated by indenting on a calibration sample. The determination of the indentation modulus of Au(111) is beyond the scope of this work. Assuming an elasticity modulus for Au(111) EAu = 80 GPa, a Poisson's ratio νAu = 0.45, and a tip Enc-diamond = 759 GPa and νnc-diamond = 0.003, we calculate from 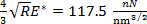 a tip radius R ≈ 1 nm. The derived value is far too low to be credible, as already pointed out in Ref. 8. It has been suggested that the elasticity modulus of metals decreases in near the surface region10. Using the value suggested in Ref. 8 (E = 30 GPa), we obtain R = 5.5 nm. Also, the Hertzian fit function used in Figure 4(b) assumes a spherical tip geometry. However, this assumption only applies to the very apex of the indenting tip, i.e., for tip displacement within the elastic deformation regime. As seen below, for larger displacements, the tip can no longer be considered as spherical but rather resembles a Berkovich tip. Note further that the Hertzian fit curve is extended beyond the elastic regime so as to calculate the work of plasticity Wplasticity from the integrated difference between the Hertzian fitting curve and the experimental result21; Wplasticity = 11.44 x 10-15 J. A magnified view of the force-penetration curve shown in Figure 4(b) further demonstrates the outstanding resolution of the method to detect single atomistic plasticity events with pop-in lengths of the same order of magnitude as the Burger's vector of gold.
a tip radius R ≈ 1 nm. The derived value is far too low to be credible, as already pointed out in Ref. 8. It has been suggested that the elasticity modulus of metals decreases in near the surface region10. Using the value suggested in Ref. 8 (E = 30 GPa), we obtain R = 5.5 nm. Also, the Hertzian fit function used in Figure 4(b) assumes a spherical tip geometry. However, this assumption only applies to the very apex of the indenting tip, i.e., for tip displacement within the elastic deformation regime. As seen below, for larger displacements, the tip can no longer be considered as spherical but rather resembles a Berkovich tip. Note further that the Hertzian fit curve is extended beyond the elastic regime so as to calculate the work of plasticity Wplasticity from the integrated difference between the Hertzian fitting curve and the experimental result21; Wplasticity = 11.44 x 10-15 J. A magnified view of the force-penetration curve shown in Figure 4(b) further demonstrates the outstanding resolution of the method to detect single atomistic plasticity events with pop-in lengths of the same order of magnitude as the Burger's vector of gold.
Moreover, the shape of the AFM tip was estimated from the non-contact AFM images, shown in Figure 2(d – f), using the free SPM data analysis software Gwyddion (see Figure 5(a – c)). Subsequently, an averaged tip shape was calculated, from which the half-opening angle of the indenter was determined to be α = 67.21° (see Figure 5(d)). Together with the tip displacement values shown in Figure 4, a hardness value 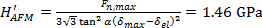 was determined, where δmax = 18 nm is the maximal tip displacement. Both hardness calculations deliver virtually the same value: HAu(111) = 1.5 GPa. This result is in good agreement with reported values for gold thin-films as measured by nanoindentation, HNI/Au = 1 – 2.5 GPa24, 25. The mean pressure at the first plasticity event during AFM indentation on Au(111) has been found to be
was determined, where δmax = 18 nm is the maximal tip displacement. Both hardness calculations deliver virtually the same value: HAu(111) = 1.5 GPa. This result is in good agreement with reported values for gold thin-films as measured by nanoindentation, HNI/Au = 1 – 2.5 GPa24, 25. The mean pressure at the first plasticity event during AFM indentation on Au(111) has been found to be 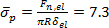 GPa4. From our experimental values and together with the estimated tip radius, we find
GPa4. From our experimental values and together with the estimated tip radius, we find 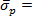 13.7 GPa. This value corresponds to a critical shear stress
13.7 GPa. This value corresponds to a critical shear stress 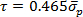 21. From our data, we find that τ = 6.3 GPa, which is in the range of values found by Asenjo et al.8 but is much larger than those found in previous studies, where τ = 1.7 – 3.4 GPa4, 26, 27. However, this value is overestimated by the lower value of the assumed tip radius, and it is reasonable to assume that the critical shear stress at the first plasticity event is bounded by the theoretical strength τtheo,Au = 4.3 GPa.
21. From our data, we find that τ = 6.3 GPa, which is in the range of values found by Asenjo et al.8 but is much larger than those found in previous studies, where τ = 1.7 – 3.4 GPa4, 26, 27. However, this value is overestimated by the lower value of the assumed tip radius, and it is reasonable to assume that the critical shear stress at the first plasticity event is bounded by the theoretical strength τtheo,Au = 4.3 GPa.
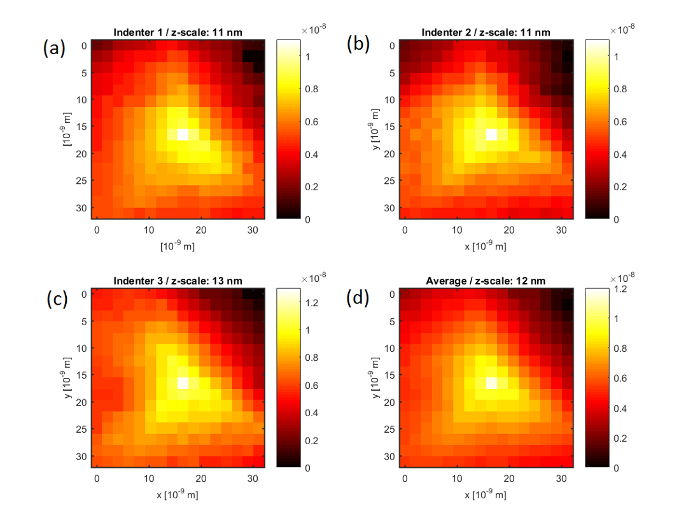
Figure 5: Tip reconstruction from non-contact AFM topography images of AFM indents on an atomically smooth gold thin-film surface. (a – c) Reconstructed tip shapes calculated from the non-contact AFM images shown in Figure 2(d – f) using the free SPM analysis software Gwyddion. (d) Averaged tip shape from the images shown in (a – c). From (d), the half-opening angle of the indenter is determined to be α = 67.21°; together with the tip displacement values shown in Figure 4, a hardness value 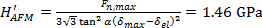 was determined, where Fn,max = 7.2 µN is the maximal vertical force and δmax = 18 nm is the maximal tip displacement. Please click here to view a larger version of this figure.
was determined, where Fn,max = 7.2 µN is the maximal vertical force and δmax = 18 nm is the maximal tip displacement. Please click here to view a larger version of this figure.
Discussion
A method has been presented for performing a series of indentations on an Au(111) thin-film surface with a diamond-coated AFM tip. Non-contact AFM imaging and AFM indentation were performed with the same force sensor. The requirements for non-contact imaging are a high first free resonance frequency f0,1 ≥ 180 kHz and a high quality factor Q ≥ 300. In AFM indentation, the vertical force to be applied is in the range of several micro-newtons, and a cantilever with a high bending stiffness is required. An additional requirement of the cantilever tip is that it is mechanically stable and wear-resistant. These requirements are fulfilled by diamond-coated cantilevers. In this experiment, a cantilever of the type CDT-NCLR was selected.
The results presented here are found to be well-reproducible. In particular, the shapes of the indents in the non-contact AFM images are invariant upon measurement repetition, and the corresponding force-displacement curves show a very good overlap. However, to ensure good reproducibility, it is critical to minimize the instrumental thermal drift and scanner creep effects. This is can be achieved by letting the instrument stabilize during image scanning prior to indentation and by subsequently monitoring the scanner position until it does not significantly change. The drift and creep effects can further be minimized by performing the displacement-controlled indentation at a high displacement rate. In the presented experiment, the displacement rate was set to 300 nm/sec. Furthermore, some instruments allow for a reduction in the range of the z-scanner by reducing the maximum applicable voltage. If available, this option should be selected, since the time for the scanner to stabilize reduces with its displacement range.
As demonstrated above, the presented technique is suitable to assess the mechanical properties of soft metals and other soft materials, such as polymers. The advantage of this technique over conventional indentation techniques, such as nanoindentation, comes from the higher depth- and force-resolution of AFM instruments and from the reduced size of the indenter that altogether allow for the observation of single atomistic plasticity events and for the determination of hardness at the true nanometer scale. On the other hand, for samples with a high level of hardness, the geometry may change upon measuring, making a direct comparison between different measurements difficult. In the case of metals, a diamond-coated AFM tip has proven to provide reproducible results on different samples over several series of indentations11. A typical force-displacement curve was fitted with a Hertzian function within its elastic regime and further extended to calculate the work of plasticity. The extraction of the indentation modulus for Au(111), however, remains uncertain, since neither the radius at the tip apex nor the indentation modulus of the diamond-coated tip are precise enough to characterize. Nevertheless, an elucidation of this limitation is beyond the scope of this work.
Due to tip convolution effects, the indent area tends to be underestimated during AFM imaging, so the presented technique provides slightly overestimated values for hardness11. This technique can be applied to the measurement of thin film, where the indentation depth should be kept ten times smaller than the film thickness in order to avoid substrate effects.
To conclude, an experimental procedure to reproducibly measure hardness at the true nanometer scale and to observe single atomistic plasticity events has been presented.
Divulgaciones
The authors have nothing to disclose.
Acknowledgements
A.C. is grateful to KoreaTech for financial support.
Materials
| AFM XE-100 | Park Instruments | discontinued | Atomic force microscope |
| CDT-NCLR | NanoSensors | CDT-NCLR | Conductive diamond coated non-contact lever |
| 100 nm thick Au(111) thin film on Mica | Phasis | 20020011 | atomically smooth gold thin film |
Referencias
- Tabor, D. . The hardness of metals. , (1951).
- Fischer-Cripps, A. C. . Nanoindentation. , (2004).
- Michalke, T. A., Houston, J. E. Dislocation Nucleation at Nano-Scale Mechanical Contacts. Acta Mater. 46 (2), 391-396 (1998).
- Kiely, J. D., Houston, J. E. Nanomechanical Properties of Au(111) (001), and (110) Surfaces. Phys. Rev. B. 57 (19), 12588 (1998).
- Kiely, J. D., Jarausch, K. F., Houston, J. E., Russell, P. E. Initial Stages of Yield in Nanoindentation. J. Mater. Res. 14 (19), 2219-2227 (1999).
- Egberts, P., Bennewitz, R. Atomic Scale Nanoindentation: Detection and Indentification of Single Glide Events in Three Dimensions by Force Microscopy. Nanotechnology. 22 (42), 425703-1-425703-9 (2011).
- Filleter, T., Bennewitz, R. Nanometer Scale Plasticity of Cu(100). Nanotechnology. 18 (4), 044004-1-044004-4 (2007).
- Asenjo, A., Jaafar, M., Carrasco, E., Rojo, J. M. Dislocation mechanisms in the first stage of plasticity of nanoindented Au(111) surfaces. Phys. Rev. B. 73 (7), 075431 (2006).
- Paul, W., Oliver, D., Miyahara, Y., Gruetter, P. Minimum threshold for incipient plasticity in the atomic-scale nanoindentation of Au(111). Phys. Rev. Lett. 110 (13), 135506 (2013).
- Kracke, B., Damaschke, B. Measurement of nanohardness and nanoelasticity of thin gold films with scanning force microscope. Appl. Phys. Lett. 77 (3), 361-363 (2000).
- Sansoz, F., Gang, T. A force-mapping method for quantitative hardness measurements by atomic force microscopy with diamond-tipped sapphire cantilevers. Ultramicroscopy. 111, 11-19 (2010).
- Silva, E. C. C. M., Van Vliet, K. J. Robust approach to maximize the range and accuracy of force application in atomic force microscopes with non-linear position-sensitive detectors. Nanotechnolgy. 17 (21), 5525-5529 (2006).
- Caron, A., Bennewitz, R. Lower Nanometer-Scale Size Limit for the Deformation of a Metallic Glass by Shear Transformations Revealed by Quantitative AFM Indentation. Beilstein J. Nanotechnol. 6, 1721-1732 (2015).
- Andriotis, O. G., et al. Nanomechanical assesment of human and murine collagen fibrils via atomic force microscopy cantilever-based nanoindentation. J. Mech. Behavior Biomed. Mater. 39, 9-26 (2014).
- Bischel, M. S., Vanlandingham, M. R., Eduljee, R. F., Gillespie, J. W., Schultz, J. M. On the use of nanoscale indentation with the AFM in the identification of phases in blends of linear low density polyethylene and high density polyethylene. J. Mater. Sci. 35 (1), 221-228 (2000).
- Zhang, L., Wang, W., Zheng, L., Wang, X., Yan, Q. Quantitative characterization of mechanical property of annealed monolayer colloidal crystal. Langmuir. 32 (2), 451-459 (2016).
- Nečas, D., Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 10 (1), 181-188 (2012).
- Hahn, B. H., Valentine, D. T. . Essential Matlab for Engineers and Scientists. , (2013).
- Nonnenmacher, M., Greschner, J., Wolter, O., Kassing, R. Scanning Force Microscopy with Micromachined Silicon Sensors. J. Vac. Sci. Technol. B. 9 (2), 1358-1362 (1991).
- Cannara, R. J., Brukman, M. J., Carpick, R. W. Cantilever tilt compensation for variable-load atomic force microscopy. Rev. Sci. Instrum. 76 (5), 053706 (2005).
- Johnson, K. L. . Contact Mechanics. , (1985).
- Mohr, M., et al. Young’s Modulus, Fracture Strength, and Poisson’s Ratio of Nanocrystalline Diamond Films. J. Appl. Phys. 116 (12), 124308-1-124308-10 (2014).
- Arnault, J. C., Mosser, A., Zamfirescu, M., Pelletier, H. Elastic recovery measurements performed by atomic force microscopy and standard nanoindentation on a Co(10.1) monocrystal. J. Mater. Res. 17 (6), 1258-1265 (2002).
- Cao, Y., et al. Nanoindentation measurements of the mechanical properties of polycrystalline Au and Ag thin films on silicon substrates: Effect of grain size and film thickness. Mater. Sci. Eng. A. 457 (1-2), 232-240 (2006).
- Lilleodden, E. T., Nix, W. D. Microstructural length-scale effects in the nanoindentation behavior of thin gold films. Acta Mater. 54 (6), 1583-1593 (2006).
- Corcoran, S. G., Colton, R. J., Lilleodden, E. T., Gerberich, W. W. Anomalous plastic deformation at surfaces: Nanoindentation of gold single crystals. Phys. Rev. B. 55 (24), R16057 (1997).
- Van Vliet, K. J., Li, J., Zhu, T., Yip, S., Suresh, S. Quantifying the early stages of plasticity through nanoscale experiments and simulations. Phy. Rev. B. 67 (10), 104105 (2003).

