Entropie

Les particules de sel qui se sont dissoutes dans l’eau ne se remettent jamais spontanément ensemble en solution pour reformer des particules solides. En outre, un gaz qui s’est détendu dans le vide reste dispersé et ne se réassemble jamais spontanément. La nature unidirectionnelle de ces phénomènes est le résultat d’une fonction d’état thermodynamique appelée entropie (S). L’entropie est la mesure dans laquelle l’énergie est dispersée dans un système ou, en d’autres termes, elle est proportionnelle au degré de désordre d’un système thermodynamique. L’entropie peut augmenter (ΔS > 0, le désordre augmente) ou diminuer (ΔS < 0, le désordre diminue) en raison de transformations physiques ou chimiques dans le système. La variation d’entropie est la différence entre les entropies des états final et initial : ΔS = S_f –S_i.

La théorie des micro-états de Boltzmann

Un état microscopique est une configuration précise de tous les emplacements et toutes les énergies des atomes ou molécules qui composent un système. La relation entre l’entropie d’un système et le nombre de micro-états possibles (W) est S = k ln W, où k est la constante de Boltzmann, 1,38 × 10⁻²³ J/K.

La variation d’entropie est

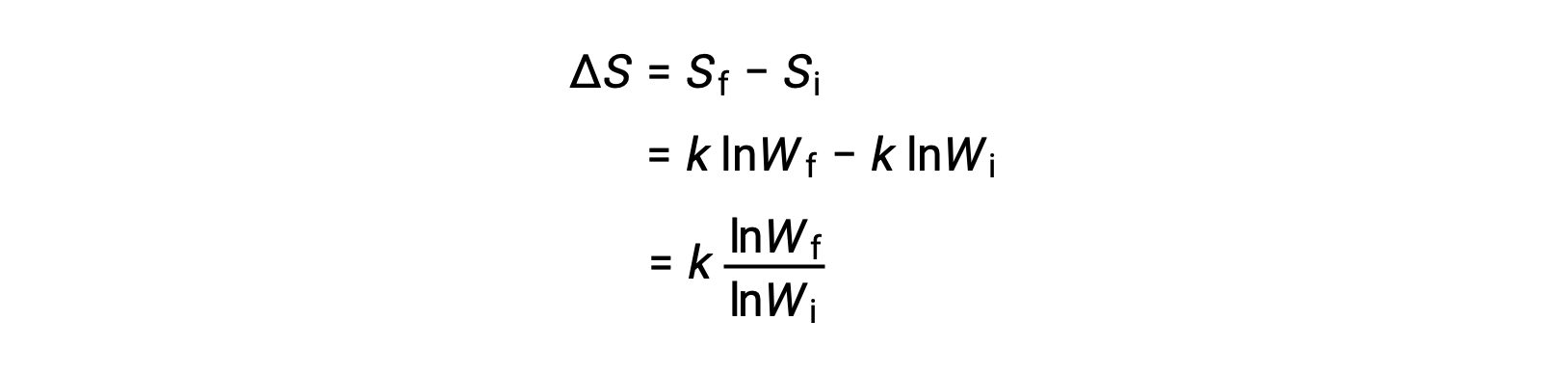
Un système qui a un plus grand nombre de micro-états possibles est plus désordonné (entropie plus élevée) qu’un système ordonné (entropie plus faible) avec un nombre moins grand de micro-états. Pour les processus impliquant une augmentation du nombre de micro-états, W_f > W_i, l’entropie du système augmente et ΔS > 0. Inversement, les processus qui réduisent le nombre de micro-états, W_f < W_i, produisent une diminution de l’entropie du système, ΔS < 0.

Envisagez la répartition d’un gaz parfait entre deux fioles connectées. Au départ, les molécules de gaz sont confinées à une seule des deux fioles. L’ouverture de la vanne entre les fioles augmente le volume dont disposent les molécules de gaz (l’énergie est plus dispersée dans un domaine plus grand) et, par conséquent, le nombre de micro-états possibles pour le système. Puisque W_f > W_i, le processus d’expansion implique une augmentation de l’entropie (ΔS > 0) et il est spontané.

Une approche similaire peut être utilisée pour décrire le flux spontané de chaleur. Une tasse de thé chaude disperse uniformément son énergie sur un plus grand nombre de particules d’air dans la pièce plus froide, ce qui entraîne un plus grand nombre de micro-états.

Généralisations concernant l’entropie

Les relations entre l’entropie, les micro-états et la dispersion de la matière et de l’énergie permettent de faire des généralisations à propos des entropies relatives des substances et de prévoir le signe des variations d’entropie pour les processus chimiques et physiques.

Dans la phase solide, les atomes ou les molécules sont limités à des positions presque fixes les uns par rapport aux autres et ne sont capables que de modestes oscillations sur ces positions. Ainsi, le nombre de micro-états est relativement faible. Dans la phase liquide, les atomes ou molécules peuvent se déplacer librement les uns autour des autres, bien qu’ils restent relativement proches les uns des autres. Ainsi, le nombre de micro-états est proportionnellement plus grand que pour le solide. Par conséquent, S_liquide > S_solide et le processus de conversion d’une substance de solide à liquide (fusion) est caractérisé par une augmentation de l’entropie, ΔS > 0. Selon la même logique, le processus réciproque (gel) présente une diminution de l’entropie, ΔS < 0.

 En phase gazeuse,  un nombre donné d’atomes ou de molécules occupent un volume beaucoup plus important que la phase liquide, ce qui correspond à un nombre beaucoup plus grand de micro-états. Par conséquent, pour toute substance, S_gaz > S_liquide > S_solide et les processus de vaporisation et de sublimation impliquent également des augmentations de l’entropie, ΔS > 0. De même, les transitions de phase réciproque — condensation et dépôt — impliquent des diminutions de l’entropie, ΔS < 0.

D’après la théorie cinétique-moléculaire, la température d’une substance est proportionnelle à l’énergie cinétique moyenne de ses particules. L’augmentation de la température d’une substance entraîne des vibrations plus étendues des particules dans les solides et des mouvements plus rapides des particules dans les liquides et les gaz. À des températures plus élevées, la distribution des énergies cinétiques entre les atomes ou les molécules de la substance est également plus dispersée qu’à des températures plus basses. Ainsi, l’entropie de n’importe quelle substance augmente avec la température.

L’entropie d’une substance est influencée par la structure des particules (atomes ou molécules) qui constituent la substance. En ce qui concerne les substances atomiques, les atomes plus lourds possèdent une entropie plus grande à une température donnée que les atomes plus légers, ce qui est une conséquence de la relation entre la masse d’une particule et l’espacement des niveaux d’énergie de transition quantifiée. Pour les molécules, un plus grand nombre d’atomes augmente le nombre de façons dont les molécules peuvent vibrer et donc le nombre de micro-états possibles ainsi que l’entropie du système.

Enfin, les variations des types de particules influent sur l’entropie d’un système. Par rapport à une substance pure, dans laquelle toutes les particules sont identiques, l’entropie d’un mélange de deux ou plusieurs types de particules différents est plus grande. Ceci est dû aux orientations et interactions supplémentaires possibles dans un système composé de constituants non identiques. Par exemple, lorsqu’un solide se dissout dans un liquide, les particules du solide jouissent d’une plus grande liberté de mouvement et d’interactions supplémentaires avec les particules de solvant. Cela correspond à une dispersion plus uniforme de la matière et de l’énergie et à un plus grand nombre de micro-états. Le processus de dissolution implique donc une augmentation de l’entropie, ΔS > 0.

Ce texte est adapté de Openstax, Chimie 2e, Chapitre 16.2 : Entropie.