Three-Dimensional Mapping of the Rotation of Interactive Virtual Objects with Eye-Tracking Data

Rodrigo A. Consoli; Eduardo Colli; Raimundo da Silva Soares Jr.; Jo&#227;o R. Sato; Guilherme A. Marson

doi:10.3791/65977

JoVE Journal > Neuroscience

Neuroscience

Three-Dimensional Mapping of the Rotation of Interactive Virtual Objects with Eye-Tracking Data

Published: October 18, 2024

doi:

10.3791/65977

Rodrigo A. Consoli¹, Eduardo Colli², Raimundo da Silva Soares Jr.^3,4, João R. Sato³, Guilherme A. Marson¹

¹Graduate Program in Chemistry,University of São Paulo, Institute of Chemistry, ²Graduate Program in Applied Mathematics,University of São Paulo, Institute of Mathematics and Statistics, ³Graduate Program in Neuroscience and Cognition,Federal University of ABC, Center of Mathematics, Computing and Cognition, ⁴School of Biomedical Engineering, Science and Health Systems,Drexel University

Summary

We have developed a simple, customizable, and efficient method for recording quantitative processual data from interactive spatial tasks and mapping these rotation data with eye-tracking data.

Abstract

We present a method for real-time recording of human interaction with three-dimensional (3D) virtual objects. The approach consists of associating rotation data of the manipulated object with behavioral measures, such as eye tracking, to make better inferences about the underlying cognitive processes.

The task consists of displaying two identical models of the same 3D object (a molecule), presented on a computer screen: a rotating, interactive object (iObj) and a static, target object (tObj). Participants must rotate iObj using the mouse until they consider its orientation to be identical to that of tObj. The computer tracks all interaction data in real time. The participant's gaze data are also recorded using an eye tracker. The measurement frequency is 10 Hz on the computer and 60 Hz on the eye tracker.

The orientation data of iObj with respect to tObj are recorded in rotation quaternions. The gaze data are synchronized to the orientation of iObj and referenced using this same system. This method enables us to obtain the following visualizations of the human interaction process with iObj and tObj: (1) angular disparity synchronized with other time-dependent data; (2) 3D rotation trajectory inside what we decided to call a "ball of rotations"; (3) 3D fixation heatmap. All steps of the protocol have used free software, such as GNU Octave and Jmol, and all scripts are available as supplementary material.

With this approach, we can conduct detailed quantitative studies of the task-solving process involving mental or physical rotations, rather than only the outcome reached. It is possible to measure precisely how important each part of the 3D models is for the participant in solving tasks, and thus relate the models to relevant variables such as the characteristics of the objects, cognitive abilities of the individuals, and the characteristics of human-machine interface.

Introduction

Mental rotation (MR) is a cognitive ability that enables individuals to mentally manipulate and rotate objects, facilitating a better understanding of their features and spatial relationships. It is one of the visuospatial abilities, a fundamental cognitive group that was studied as early as 1890¹. Visuospatial abilities are an important component of an individual's cognitive repertoire that is influenced by both inherited and environmental factors²^,³^,⁴^,⁵. Interest in visuospatial abilities has grown throughout the twentieth century due to mounting evidence of their importance in key subjects such as aging⁶ and development⁷, performance in science, technology, engineering, and mathematics (STEM)⁸^,⁹, creativity¹⁰, and evolutionary traits¹¹.

The contemporary idea of MR derives from the pioneering work published by Shepard and Metzler (SM) in 1971¹². They devised a chronometric method using a series of "same or different" tasks, presenting two projections of abstract 3D objects displayed side by side. Participants had to mentally rotate the objects on some axis and decide if those projections portrayed the same object rotated differently or distinct objects. The study revealed a positive linear correlation between response time (RT) and the angular disparity (AD) between representations of the same object. This correlation is known as the angle disparity effect (ADE). ADE is regarded as a behavioral manifestation of MR and became ubiquitous in several influential subsequent studies in the field¹³^,¹⁴^,¹⁵^,¹⁶^,¹⁷^,¹⁸^,¹⁹^,²⁰^,²¹^,²²^,²³^,²⁴^,²⁵. The 3D objects employed in the SM study were composed of 10 contiguous cubes generated by the computer graph pioneer Michael Noll at Bell Laboratories²⁶. They are referred to as SM figures and are widely employed in MR studies.

Two advancements were of great importance in Shepard and Metzler's seminal work; first, considering the contributions in the field of MR assessments. In 1978, Vanderberg and Kuze²⁷ developed a psychometric 20-item pencil-and-paper test based on SM "same or different" figures that became known as the mental rotation test (VKMRT). Each test item presents a target stimulus. Participants must select among four stimuli, which ones represent the same object depicted in the target stimulus, and which do not. VKMRT has been used to investigate the correlation between MR ability and various other factors, such as sex-related differences⁶^,²¹^,²⁴^,²⁸^,²⁹^,³⁰, aging and development⁶^,³¹^,³², academic performance⁸^,³³, and skills in music and sports³⁴. In 1995, Peters et al. published a study with redrawn figures for the VKMRT³⁵^,³⁶. Similarly, following the "same or different" task design, a variety of other libraries of computer-generated stimuli have been employed to investigate MR processes and to assess MR abilities (3D versions of the original SM stimuli¹⁹^,²²^,²³^,³⁷^,³⁸, human body mimicking SM figures²⁵^,³⁹^,⁴⁰, flat polygons for 2D rotation⁴¹^,⁴², anatomy, and organs⁴³, organic shapes⁴⁴, molecules⁴⁵^,⁴⁶, among others²¹). The Purdue Spatial Visualization Test (PSVT) proposed by Guay in 1976⁴⁷ is also relevant. It entails a battery of tests, including MR (PSVT:R). Employing different stimuli from those in VKMRT, PSVT:R requires participants to identify a rotation operation in a model stimulus and mentally apply it to a different one. PSVT:R is also widely used, particularly in studies investigating the role of MR in STEM achievement⁴⁸^,⁴⁹^,⁵⁰.

The second advancement of great importance in Shepard and Metzler's seminal work comprises the contributions to the understanding of the MR process, in particular, with the use of eye-tracking devices. In 1976, Just and Carpenter¹⁴ used analog video-based eye-tracking equipment to conduct a study based on Shepard and Metzler's ADE experiment. From their results on saccadic eye movements and RTs, they proposed a model of MR processes consisting of three phases: 1) the search phase, in which similar parts of the figures are recognized; 2) the transformation and comparison phase, in which one of the identified parts is mentally rotated; 3) the confirmation phase, in which it is decided whether the figures are the same or not. The phases are repeated recursively until a decision can be made. Each step corresponds to specific saccadic and fixational eye movement patterns in close relation to observed ADEs. Thus, by correlating eye activity to chronometric data, Just and Carpenter provided a cognitive signature for the study of MR processes. To date, this model, albeit with adaptations, has been adopted in several studies¹⁵^,⁴²^,⁴⁶^,⁵¹^,⁵²^,⁵³.

Following this track, several ensuing studies monitoring behavioral¹⁸^,¹⁹^,²²^,²³^,²⁵^,³⁴^,⁴⁰^,⁵⁴^,⁵⁵ and brain activity²⁰^,²²^,⁵⁶^,⁵⁷ functions during stimuli rotation were conducted. Their findings point to a cooperative role between MR and motor processes. Moreover, there is a growing interest in investigating problem-solving strategies involving MR in relation to individual differences ¹⁵^,⁴¹^,⁴⁶^,⁵¹^,⁵⁸.

Overall, it can be considered that the design of studies aiming at understanding MR processes is based on presenting a task with visual stimuli that requests participants to perform an MR operation that, in turn, entails a motor reaction. If this reaction allows rotation of the stimuli, it is often called physical rotation (PR). Depending on the specific objectives of each study, different strategies and devices have been employed for data acquisition and analysis of MR and PR. In the task stimulus presentation step, it is possible to change the types of stimuli (i.e., previously cited examples); the projection (computer-generated images in traditional displays²²^,²³^,²⁵^,²⁹^,⁴⁰^,⁴¹^,⁵⁹, as well as in stereoscopes¹⁹ and virtual⁶⁰ and mixed⁴³ reality environments); and the interactivity of the stimuli (static images¹²^,²⁷^,³⁶, animations⁶¹, and interactive virtual objects¹⁹^,²²^,²³^,⁴³^,⁵³^,⁵⁹).

MR is usually inferred from measures of RTs (ADE), as well as ocular and brain activity²⁵^,⁴⁶^,⁶². Ocular activity is measured using eye-tracking data consisting of saccadic movements and fixations¹⁴^,¹⁵^,⁴²^,⁵¹^,⁵²^,⁵⁴^,⁵⁸^,⁶⁰, as well as pupillometry⁴⁰. RT data typically arise from motor response data recorded while operating various devices such as levers¹³, buttons and switches¹⁴^,⁵³, pedals⁵³, rotary knobs¹⁹, joysticks³⁷, keyboard⁶¹ and mouse²⁹^,⁵⁸^,⁶⁰, drive wheels⁵³, inertial sensors²²^,²³, touch screens⁵²^,⁵⁹, and microphones²². To measure PR, in addition to the RTs, the study design will also include recording manual rotations of interactive stimuli while participants perform the MR task²²^,²³^,⁵²^,⁵³.

In 1998, Wohlschläger and Wohlschläger¹⁹ used "same or different" tasks with interactive virtual SM stimuli manipulated with a knob, with rotations limited to one axis per task. They measured RT and the cumulative record of physical rotations performed during the tasks. Comparing situations with and without actual rotation of the interactive stimuli, they concluded that MR and PR share a common process for both imagined and actually performed rotations.

In 2014, two studies were conducted employing the same type of tasks with virtual interactive stimuli²²^,²³. However, the objects were manipulated with inertial sensors that captured motion in 3D space. In both cases, in addition to RTs, rotation trajectories were recorded – the evolution of rotation differences between reference and interactive stimuli during the tasks. From these trajectories, it was possible to extract both cumulative information (i.e., the total number of rotations, in quaternionic units) and detailed information about solution strategies. Adams et al.²³ studied the cooperative effect between MR and PR. In addition to RTs, they used the integral of the rotation trajectories as a parameter of accuracy and objectivity of resolution. Curve profiles were interpreted according to a three-step model⁶³ (planning, major rotation, fine adjustment). The results indicate that MR and PR do not necessarily have a single, common factor. Gardony et al.²² collected data on RT, accuracy, and real-time rotation. In addition to confirming the relationship between MR and PR, the analysis of rotation trajectories revealed that participants manipulated the figures until they could identify whether they were different or not. If they were the same, participants would rotate them until they looked the same.

Continuing this strategy, in 2018, Wetzel and Bertel⁵² also used interactive SM figures in "same or different" tasks using touchscreen tablets as the interface. In addition, they used an eye-tracking device to obtain cumulative data on fixation time and saccadic amplitude as parameters of the cognitive load involved in solving MR tasks. The authors confirmed the previous studies discussed above regarding the relationships between MR and PR and the task-solving processes. However, in this study, they did not use fixation mapping and saccades data for the stimuli.

Methodological approaches for mapping eye-tracking data over virtual 3D objects have been proposed and constantly improved, commonly by researchers interested in studying the factors related to visual attention in virtual environments⁶⁴. Although affordable and using similar eye-tracking devices, apparently, these methods have not been effectively integrated into the experimental repertoire employed in mental rotation studies with interactive 3D objects such as those previously mentioned. Conversely, we did not find any studies in the literature reporting real-time mapping of fixation and saccade motion data on interactive 3D objects. There seems to be no convenient method to integrate eye-activity data with rotation trajectories easily. In this research, we aim to contribute to filling this gap. The procedure is presented in detail, from data acquisition to graphical output generation.

In this paper, we describe in detail a method for studying mental rotation processes with virtual interactive 3D objects. The following advances are highlighted. First, it integrates quantitative behavioral motor (hand-driven object rotation via a computer interface) and ocular (eye-tracking) data collection during interaction sessions with 3D virtual models. Second, it requires only conventional computer equipment and eye-tracking devices for visual task design, data acquisition, recording, and processing. Third, it easily generates graphical output to facilitate data analysis – angular disparity, physical rotation, quaternionic rotation trajectories, and hit mapping of eye-tracking data over 3D virtual objects. Finally, the method requires only free software. All developed code and scripts are available free of charge (https://github.com/rodrigocnstest/rodrigocnstest.github.io).

Protocol

1. Preparation of data collection tools

Set up the online data collection (optional).
NOTE: This step describes how to set up a customizable clone of the project code and working webpage (refer to Supplemental File 1). This step was adapted from the tutorials available at https://pages.github.com/ and https://github.com/jamiewilson/form-to-google-sheets. If users are only interested in the data processing method and not in the data recording, they can use the webpage https://rodrigocnstest.github.io/iRT_JoVE.html, together with Supplemental Table S1 and the repository files at https://github.com/rodrigocns/rodrigocns_JoVE/tree/main/Octave, and skip steps 1.1, 1.2, and its substeps.
1. Sign in at GitHub (https://github.com/).
2. Create a public clone of the original GitHub pages repository.
  1. Click on Import repository from https://github.com while logged into the account.
  2. In the Your old repository's clone URL field, paste the URL https://github.com/rodrigocns/rodrigocns_JoVE in the Repository name field, type in username.github.io, where username is the username used in the account, and ensure the Public option is enabled. Then, click on the green button Begin import.
    NOTE: The repository now contains most of the files needed for the remainder of this setup, and any changes made to the repository will be updated on the website after a couple of minutes. As an example, the user named rodrigocnstest would access their own page at https://rodrigocnstest.github.io and their GitHub repository at https://github.com/rodrigocnstest/rodrigocnstest.github.io.
3. Set up a cloud spreadsheet to store the experiment data online.
  1. Sign up or sign into a Google account.
  2. While logged into the account, go to the iRT spreadsheets clean file available at https://docs.google.com/spreadsheets/d/1imsVR7Avn69jSRV8wZYfsPkxvhSPZ73X_9
    Ops1wZrXI/edit?usp=sharing.
  3. Inside this spreadsheet, click on File | Make a copy. A small confirmation window will appear.
  4. Inside the small window, give the file a name and click on the Make a copy button.
4. Set up a Google Apps Script to automate the data storage inside the spreadsheet you created.
  1. While inside the spreadsheet file, click on the option Extension | Apps Script.
    NOTE: This script must be created or accessed from inside the spreadsheet so that it is associated with it. Attempting to create a script externally might not work.
  2. Click on the Run button to run the script for the first time.
  3. Click on the Review permissions button. A new window will appear. Click on the same account used when creating the spreadsheet.
    NOTE: If this is the first time performing this step, a safety alert may appear warning the user about the app requesting access to information from the account. It is safe as the app is trying to reach the spreadsheet contents and asking permission to fill it with data. If no warnings appear, step 1.1.4.4 can be skipped.
  4. Click on Advanced | Go to From iRT to sheets (unsafe) | Allow button.
    NOTE: After the execution, a notice saying the execution was completed should appear inside the execution log.
  5. In the left sliding panel, click on the Triggers button (the fourth icon from top to bottom) | + Add Trigger button.
  6. Under Choose which function to run, choose doPost; under Select event source, select From spreadsheet; under Select event type, choose On form submit. Then, click Save. If any permission popups appear, follow steps 1.1.4.3-1.1.4.4. If the browser ends up blocking the popup, unblock it.
  7. Click on the Deploy dropdown button | New deployment.
  8. Hover the mouse over the gear icon and ensure the Web App option is selected.
  9. Write a description in the New description field, such as Deployment 1; in the Who has access field, select Anyone and then click on the Deploy button.
    NOTE: The purpose of the New description field is to organize one's script deployments. It can be named as the reader wishes, such as First deployment. The Execute as field should already appear as Me(email), where email is the email used until now.
  10. Inside the new popup, copy the Web app URL of the script deployment.
    NOTE: If for some reason, you end up losing the copied Web app URL, retrieve it by clicking on the Deploy dropdown menu | Manage deployments. The Web app URL should be there.
  11. Go to the page at https://github.com/rodrigocnstest/rodrigocnstest.github.io/edit/main/javascript/scripts.js where rodrigocnstest is the username used at GitHub. Replace the existing URL in line 5 for the copied Web app URL in step 1.1.4.10, and click the green button Commit changes….
    NOTE: The copied URL value should remain between single ' ' or double " "' quotation marks. Double-check that the URL copied is the right one from the Web app.
  12. Finally, click on the Commit changes confirmation button in the middle of the screen.
5. Ensure the process was completed correctly and the page is working.
  1. Go to the repository at https://github.com/username/username.github.io/, where username is the username used at GitHub, and check if the deployment has been updated after the changes made in step 1.4.14.
  2. Navigate to the webpage at https://username.github.io/iRT_JoVE, change username to the username used in GitHub and then click Next.
  3. Click Go, make any interaction by clicking and dragging the object on the right with the mouse, then click the DONE! button.
  4. Go back to the spreadsheet file configured in steps 1.1.3 and 1.1.4, and verify the presence of a newly added line of data for each time the DONE button was pressed.
Set up offline data acquisition (optional).
NOTE: The method intended for running and acquiring the interactive rotation task's (iRT) data is online through the cloud services configured in the steps described above. If desired (since the internet connection might be an issue or to have an alternative way to run it), it is also possible to run the test locally with or without an internet connection at the place where the test will be executed. The following steps are an optional alternative and describe how to achieve this. Otherwise, skip to step 1.3.
1. Access the GitHub repository at the link: https://github.com/rodrigocnstest/rodrigocnstest.github.io. Click on the green button < > Code | Download ZIP, and then, uncompress the downloaded files.
  NOTE: Changes made to the files stored locally will not change the files in the repository and vice versa. Any changes intended for both versions should be applied to both locations, either manually copying the updated files or through the use of git/GitHub desktop.
2. Get the latest version of Mozilla Firefox through the link: https://www.mozilla.org/en-US/firefox/new/.
3. Open the Mozilla Firefox browser, enter "about:config" in the URL slot, enter "security.fileuri.strict_origin_policy" in the search field, and change its value to false. NOTE: Now, Mozilla Firefox in the Windows operating system should be able to locally access the downloaded webpage files on your computer. Other browsers and operating systems can be configured to work locally, each one with its setup described at the link http://wiki.jmol.org/index.php/Troubleshooting/Local_Files.
Set up the data processing tool.
1. Download and install the latest version of GNU Octave at https://octave.org/download.
Set up the eye-tracking device.
1. Make sure that the recording system software is installed on the laptop.
2. Ensure that the research room is clean and well-organized to avoid distractions.
3. Use artificial illumination in the room to maintain consistent lighting throughout the day.
4. Install the computer on a table and ensure the participant can move the mouse comfortably.
5. Provide a comfortable chair for the participant, preferably a fixed chair, to minimize movement during the test.
6. Connect one USB cable to power the infrared illumination and another USB cable between the laptop/computer and the eye-tracker for the camera.
7. Place the eye tracker below the screen.

2. Data collection

Initialize the data collection software.
1. Run the eye-tracking software on the computer to receive data from the eye-tracker.
2. Select the option Screen Capture in the main window of the software to capture gaze during the experiment (it is also possible to use this software for heatmap visualization and raw export data).
3. Click on New Project to create a new project and project folder where the data should be saved.
4. Open the test page at https://rodrigocnstest.github.io/iRT_JoVE.html if using the one offered as an example or the page created in step 1.1. Alternatively, open the iRT_JoVE.html file locally from the previously configured browser in step 1.2.
5. If needed, fill the name and email fields to help with data identification, and tick the box to download a backup copy of the data produced.
  NOTE: If using the offline method (step 1.2), it is advisable to download the backup copies.
6. Try running the experiment once to make sure the browser will load the elements correctly, and there are no issues with the tasks presented or data acquisition.
Run the experiment.
1. Explain to the participant the purpose of the experiment, the technology used, and the inclusion/exclusion criteria. Be sure that the participant has understood everything. Have the participant fill in the Consent form.
2. Ask the participant to sit before the Eye-tracking System and get as comfortable as possible.
3. Move the chair to ensure an optimal distance between the participant and the camera (the ideal length is 65 cm from the eye-tracker to the participant's eyes).
4. Ask the participant to stay as still as possible during the experiment. Adjust the camera's height to correctly capture the participant's pupils (some software highlights the pupil to show the Corneal Reflection).
5. Click on Enable Auto Gain to optimize pupil tracking by changing the camera gain until the pupils are found (some software does not have this option).
6. Ask the participant to look at a series of dots on the screen and follow the dot's movement without moving their head.
7. Click on Calibrate to start calibration (it will ensure that the eye-tracker can track where the participant is looking at the screen).
  NOTE: The screen will go blank, and a calibration marker (dot) will move through five positions on the screen.
8. After calibration, a visual point-of-gaze estimate will be drawn on the screen to check the calibration accuracy. Ask the participant to look at a specific point on display to see if the gaze will display correctly.
9. If the calibration is unsatisfactory, adjust the camera and try the calibration again until the system tracks gaze appropriately.
10. Click on the Collect Data button on the right-hand side of the Eye tracking software (main menu) to activate the data collection mode. The real-time display of the captured screen will be presented with gaze data shown in the primary display window.
11. Click on the Gaze video button in the main menu to display the user's face captured by the eye tracker. Then, click on Start record to begin the experiment.
  NOTE: During the experiment, the participant's pupil is highlighted, and their eye is displayed as a dot moving across the laptop screen. Ensure that the eye tracker tracks the pupil and eye across the screen.
12. If the dot disappears or flickers frequently, stop the experiment and try to calibrate again.
13. Open the previously opened iRT's window and tell the participant to click Next.
14. Give the following instructions to the participant: "In this section, you will perform three rotation tasks. When you click on the GO! button, two objects will appear on opposite sides of the screen. Your goal is to rotate the object on the right until it closely matches the object on the left as best as you can. To rotate the object, click and drag your mouse over it. When you finish each of the three tasks, click on the DONE! button to conclude."
  NOTE: For each task, any iRT data beyond the 5 min mark (327^th second exactly) may be lost. As we develop the method further, this limit should be expanded.
15. At the end of the experiment, ensure the eye tracker is turned off from the extension cable and put the lens cap back on the camera.
Extract the data.
1. Once the eye-tracker data collection has been completed, click on Analyze Data to access the data collected.
2. Export a .csv file with all the data recorded for the user.
  NOTE: The first column of eye tracker data must be the UNIX epoch of the data as this is the only way to make different sets of data match correctly in time. If the file does not contain one, it should be converted from any other time standard used. The file can be in a ".csv" or ".xlsx" format.
3. If using the online version of the interactive rotation tasks page (step 1.1), open the Google Sheets file used to receive the online data (created in step 1.1.3) and download it by clicking on File | Download | Microsoft Excel (.xlsx).
  NOTE: These data are packaged to facilitate the transfer of data (each task corresponds to one line filled with data). To process the data inside, each line of packaged data must be "unpacked" first.

3. Data processing and analysis

Unpackage, merge, and process the data.
NOTE: The following steps describe how to process the data by using the scripts provided (refer to Supplemental File 2). The GNU Octave scripts will prompt the user inputs about their files. If the inputs are sent as blank, the default values, referencing the provided sample data if no user data has overwritten them, will be used instead. After the script finishes running, it can be closed.
1. Download and uncompress the repository being used (the user's own or the original at https://github.com/rodrigocns/rodrigocns_JoVE) if it has not yet been downloaded.
2. Ensure the scripts 1.unpacking_sheets.m, 2.data_merge_and_process.m, 3.3D rotational trajectory.m, and the folder models are inside the downloaded repository in the folder Octave, and move the data files downloaded from steps 2.3.2 and 2.3.3 to this same folder where the octave scripts are.
  NOTE: Any existing files already in the folder with the same names as the newly written files might be overwritten. Rename or move the files to another folder accordingly.
3. Open the script 1.unpacking_sheets.m with the GNU Octave Launcher. In the Editor tab, run the script by clicking on the green Save file and run button, to unpackage the data to a more readable structure.
  NOTE: If any of the requested data files are open locally, remember to close them before running the script. All .m script files were executed using the GNU Octave Launcher.
4. Two prompts will appear, one after the other. Input the name of the downloaded file inside the first prompt and the name of the unpackaged file inside the second field. Alternatively, leave both prompt fields blank to use the default names meant for the sample files included. Wait a few minutes (depending on the volume of data) for a popup informing the user that the process is complete and the new file has been written.
5. Open and run the script 2.data_merge_and_process.m to merge the data from both, eye tracker and iRT.
  NOTE: Although this script is complex, encompassing hundreds of lines of code, it is divided into three main sections: settings, functions, and scripts. All of them are thoroughly commented on and explained, facilitating future modifications, if necessary.
6. Four prompts will appear. Input the sessionID value, taskID value (both from the iRT data table), unpackaged iRT data filename (written in step 3.1.5), and eye tracker data filename (exported in step 2.3.2) or leave all of them blank to use the default values.
  NOTE: After some minutes, a help popup will indicate that the script completed the computation and the names of the files used and created. Three sample plots of angular disparity will appear during the script process: a simple plot, a plot with colored gaze data, and a plot with pupil diameter data. The two files created are output merge X Y.xlsx and output jmol console X Y.xlsx, where X is the sessionID value, and Y is the taskID value, both written at the beginning of step 3.1.6.
Render 3D rotation trajectory images.
1. Open and run the script 3.3D rotation trajectory.m.
2. Three prompts will appear. Input the sessionID value, taskID value, and unpackaged iRT data filename, or leave them blank to use the default values.
  NOTE: A 3D graph will appear. The rendered graph is the 3D rotation trajectory of the specified session and task.
Replay the animations.
1. To replay the participant's task interaction, first, go to the interactive task webpage, start the test (showing both 3D models), move the mouse pointer at the top-right corner of the screen until the mouse icon changes to text, as depicted in Supplemental File 2, and then click on the invisible Debug text, enabling the debug mode.
2. From the buttons that appear between the models, click on the timerStop button to interrupt the task and click on the console button to open the JSmol console of the model on the right. If the task from the interaction of interest was not the first one, click on the numbered buttons inside the top debug area to change the task that is being shown on the screen.
  NOTE: JSmol is the molecular modeling software used in the webpage.
3. Open the file output jmol console.xlsx and copy the entire page of Jmol commands.
  NOTE: Each page contains commands for a different scene or animation.
4. Inside the JSmol console, paste the list of commands copied and click the Run button or press Enter on the keyboard to execute it.
5. If desired, generate a .gif animation. Write the command capture "filename" SCRIPT "output" inside the JSmol console, where filename is the name of the .gif file to be created and output is the entire list of commands copied in step 3.3.3, keeping both inside the double quotation marks.
  NOTE: The more complex the commands get, with bigger models or more changes in time, and the less potent the specifications of the computer used, the slower the animation will become. Jmol is focused on visualizing chemical compounds and reactions, and the kind of animations produced with our research pushes the boundaries of Jmol's rendering capacities. These points should be considered and accounted for when doing any quantitative measures with this animation.

4. Task customization

NOTE: This entire section is optional and only recommended for those who like to experiment or understand how to code. Below, you will find some of the many customizable options available, and more options will become available as we develop the methods further.

Configure new or existing tasks.
1. Define how many interactive tasks will be performed by the participant and name each of them in the file object_configs.js inside the array task_list replacing the existing item names or adding more. Ensure that each name is unique as they are used later as identifiers.
2. Choose JSmol-compatible 3D coordinate files to perform the interactive tasks (http://wiki.jmol.org/index.php/File_formats). Copy these files to the models folder.
  NOTE: The scripts included in this article are optimized for asymmetric models using the .xyz file format. When choosing coordinate files, avoid rotation symmetries as they have ambiguous solutions⁶⁵.
3. Define the rendering settings for 3D objects within the prepMolecule(num) function.
  NOTE: All changes from one task to the next performed by JSmol go here: changing the color pattern, changing the size or the way graphic elements are rendered, orientation, translation, hiding parts of the object, loading new 3D models, etc. (for more examples, see https://chemapps.stolaf.edu/jmol/docs/examples/bonds.htm). Each task named in task_list corresponds to a case. Each command for JSmol to execute follows the structure: Jmol.script( jsmol_obj , " jsmol_command1; jsmol_command2 "); where jsmol_obj refers to the object being changed (jsmol_ref and jsmol_obj being the default for the target and interactive objects) followed by one or more commands separated by a ";".
Create new models.
1. Use any .xyz model downloaded online or built by molecular editors such as Avogadro (https://avogadro.cc/).

Representative Results

Evolution of angular disparity and other variables
As depicted in step 3.3.1 in Supplemental File 2, two canvases are presented to the participant on the video monitor screen, displaying copies of the same 3D virtual object in different orientations. On the left canvas, the target object (tObj) remains static and serves as the target position or tObj position. On the right canvas, the interactive object (iObj) is shown in a different position and allows the participant to move it over time around a fixed rotation center using a mouse (only rotations; translations are disabled). The task at hand involves adjusting iObj to closely match tObj based on the participant's judgment. The three 3D objects used can be seen in Figure 1. The solving process, although complex, can be meticulously recorded for subsequent analysis. This recording goes beyond mere video footage as each position over time is captured at fixed 0.1 s intervals as a quaternion, forming a time series that enables a complete reconstruction of the entire process. At any position, there exists a unique rotation around a specific axis, ranging from 0° up to 180°, that directly transforms the tObj position into the iObj position. While this rotation is abstract and unrelated to the participant's PR during the task, it accurately indicates the precise iObj position relative to tObj. AD is the angle of this rotation and may be calculated from the respective quaternion. As the iObj position approaches the tObj position, this value approaches zero.

After step 3.1.6 of the Data processing and analysis section, two files were created: output merge X Y.xlsx and output jmol console X Y.xlsx, where X is the sessionID value, and Y is the taskID value. If using the default values by leaving the input fields blank, the files should be named output merge 1682707472090 bolaBastao_c.xlsx and output jmol console 1682707472090 bolaBastao_c.xlsx. The output merge X Y.xlsx files contain the selected eye tracker data merged into the iRT data, aligned by the UNIX Epoch time, similar to Figure 2A if everything proceeded correctly, or Figure 2B if some problem occurred.

The output jmol console X Y.xlsx files contain up to five tabs filled with Jmol console commands that, when pasted to the Jmol console, will reproduce the participant's movements when solving the task: rotation replay reproduces the iObj rotations made by the participant; gaze replay int reproduces the iObj rotations with added fixation heatmap on the object in time by using a transparency/opaque scale; gaze replay tgt shows only the 3D fixation heatmap of tObj during the task; gaze frame int and gaze frame tgt show the overall fixation mapping of the whole process for both iObj and tObj. All of them are illustrated in Figure 3A–F. Jmol and JSmol are essentially identical, Jmol being the plugin based in Java programming language, and JSmol in the JavaScript programming language, both having the same functionalities and being used interchangeably.

Figure 4 illustrates the evolution of angular disparity as a function of time for six different scenarios involving two participants and three objects. The duration of the process can vary significantly depending on the participant's performance with the interactive task object. In any task completed correctly by the participant, AD tends to zero at the end. If the same graph does not exhibit this behavior, either the participant was unable to complete the task because they gave up or reached the time limit per task (approximately 5 min), or an error occurred in the data processing.

The combined results of the iObj PR records and the data obtained from the eye-tracking measurements are shown in Figure 5. The variation in the angular disparity between the target and the inertial objects as a function of time indicates three distinct stages in the process of solving the task given: initial observation of the models; ballistic rotation of the interactive model; fine-tuning of the rotation of the interactive model. Figure 5A shows the gaze alternating between the models in the initial phase and, more specifically, in the fine-tuning phase. Figure 5B shows that the pupil remains more dilated in the initial and fine-tuning phases. In the fine-tuning phase, the long fixation period on the interactive model (40-47s in Figure 5A) corresponds to a plateau in pupil diameter (40-47s, Figure 5B).

These results suggest that the data obtained with the method proposed here are consistent with the model of mental rotation problem solving proposed on the basis of gaze fixation data for static models¹⁴^,⁶⁶ and for interactive models²³. Such a model would encompass three stages: search, transformation and comparison, and confirmation of the match or mismatch between the models. In addition, the alternation of fixations between the target and interactive models in the comparison stages observed in Figure 5A is consistent with the results obtained in Sheppard and Metzler-type tests that use static images⁴²^,⁶⁶. However, in the case of interactive models, it is likely that these stages of search, transformation, comparison, and confirmation occur successively through interaction and repositioning of the interactive model.

3D rotation trajectories
Each rotation in a 3D space from 0° to 180° can be translated to a point inside a ball (which is understood as the volume inside a sphere) with a radius equal to 180°. Figure 6 demonstrates this correspondence with three example rotations. The distance of the point to the center of the ball is the iObj angle disparity from the tObj position, and the vector pointing from the center of the ball to the point is the rotation direction, the rotation being made in the clockwise sense viewing from the center. This translation of rotations into points in a ball allows someone to directly visualize, in a single 3D drawing, the entire trajectory of rotations made by the participant in a task. We call this drawing the 3D rotation trajectory.

Analogously to the AD measure, for any tasks correctly completed by the participant, the trajectory should approach, in the end, the center of the ball. If the trajectory reaches the sphere's boundary at a rotation of 180°, it will wrap around to the antipodal point on the sphere. Figure 7 illustrates the rotation trajectory taken by the two previously mentioned participants performing the third task (C1 and C2 in Figure 4), viewed both in perspective and in projections on the three coordinate planes. It is clear from the figure that, despite the relatively small starting AD close to 45°, participant 1 initially deviated from the target position before finding a definitive path to the solution, unlike participant 2, who completed the task faster.

3D Fixation heatmap
During the problem-solving process, the participant alternates their gaze between tObj and iObj while interacting with iObj. With the eye-tracking data, we can extract the participant's gaze position and create a heatmap of the screen regions that captured the most and least attention from the participant in any given interval. Going further, with both the eye-tracking and iRT quaternion data synchronized, we can simultaneously map in 3D space and in time, how much attention each of the object vertices is receiving, even for objects being rotated in time.

In Figure 3, the attention given to the object is represented by the opacity level of each vertex. The closer it is to the participant's gaze and the longer it remains in proximity, the more attention it receives, resulting in higher opacity in that region of the object. The spatial decrease in attention is modeled using a bivariate homogeneous Gaussian function for the gaze position and a simple homogeneous Gaussian function applied for the elapsed time. The standard deviation of these Gaussians was chosen assuming a visual angle of 2 degrees⁶⁷ and a visual short-term memory of 10 s⁶⁸. To prevent any visual artifacts with this method, the gaze proximity data is set to zero while the gaze is outside the object canvas (iObj receives no residual attention when the gaze is inside the tObj canvas or outside both). Figure 3 shows a single frame from each object of an entire replay animation and the same frames with the 3D fixation heatmap. A possible comparison between tObj and iObj by the participant during the solving process can be seen (Figure 3C,D) as the task is nearing its conclusion (time = 6.3 s). The whole process can be seen as a video in Supplemental Video S1. We report the results of the computer-mediated rotation of 3D models presented to participants as a task taken under ordinary conditions.

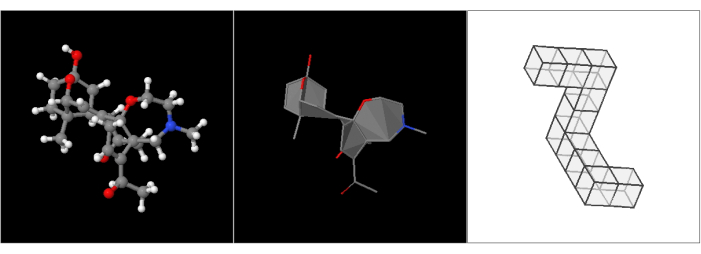
Figure 1: Target objects used. Image of the 3D models used in the webpage tasks. (A) A molecule with ball and stick representation; (B) The same molecule with filled polygons, no hydrogens, and represented by sticks only; (C) a polycube similar to one of the Shepard and Metzler figures¹³, derived from the stimuli library of Peters and Battista³⁶. Please click here to view a larger version of this figure.

Figure 2: Sheets comparison. (A,B) Images are taken from the spreadsheet output merge 1682707472090 bolaBastao_c.xlsx. Columns A to G contain iRT data values, whereas columns H to N contain eye tracker data values. In (A), everything is correct, while in (B), in the eye tracker columns, all values are constant and do not match the iRT system time values. If any problem occurs with the data synchronization process, this error will likely happen. Please click here to view a larger version of this figure.

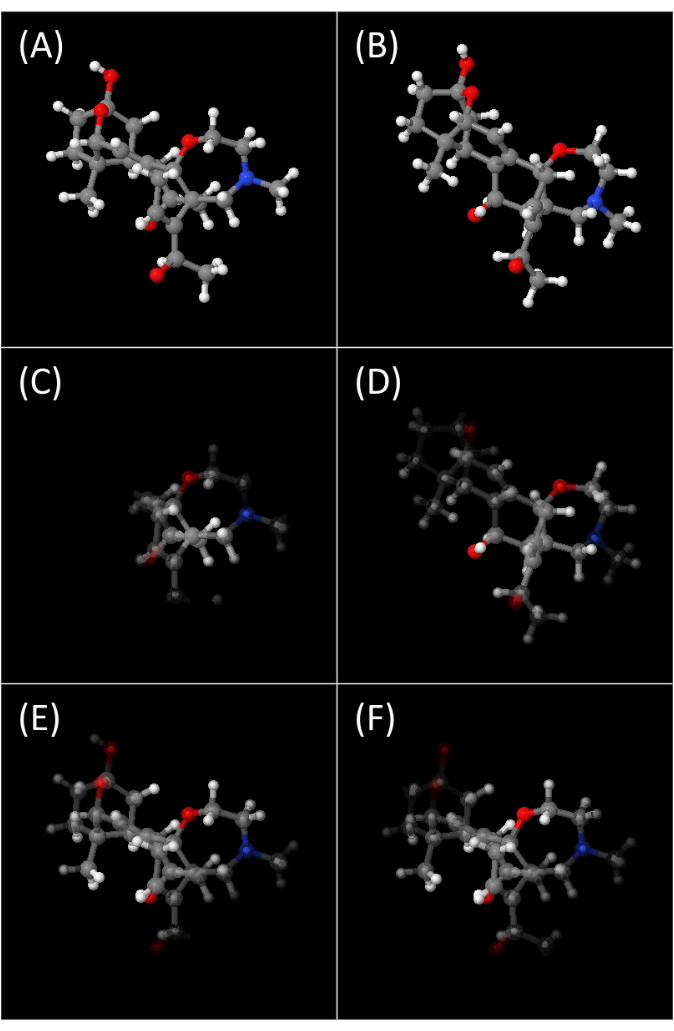
Figure 3: 3D fixation heatmap. Fixation heatmap over the 3D object using a scale of opacity, where more opaque correlates to more time spent near the participant gaze. (A,B) tObj and iObj images of the task being solved by the participant at the 6.3 s mark. (C,D) Same images as (A,B) at the same instant with the added opacity scale of the heatmap. (E,F) Fixation heatmap images considering the entire period for which the participant could see the objects. Please click here to view a larger version of this figure.

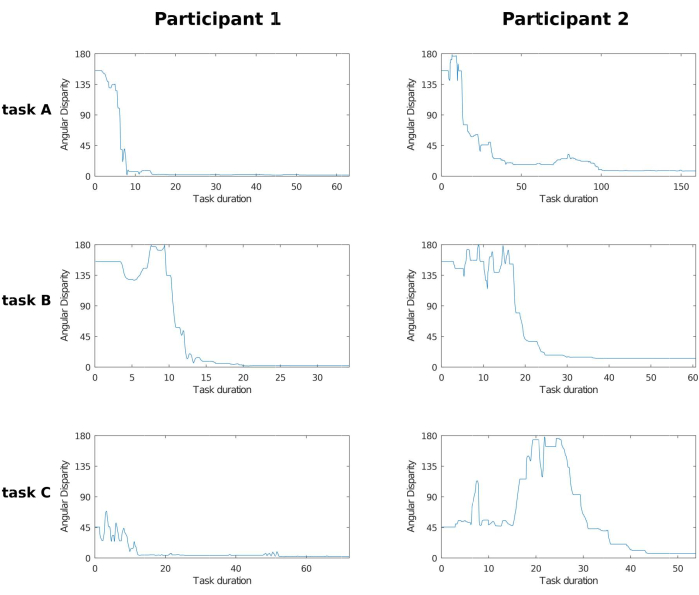
Figure 4: AD grid. Plot grid of angular disparity across two participants and three tasks. Columns represent participants 1 and 2, and rows represent the tasks solved by the participants using the three objects illustrated in Figure 3. Note that while AD varies between 0° and 180°, the time range is not fixed and varies with the participant's performance and their own decision to stop the process. As the participant rotates iObj, the AD between tObj and iObj varies as time progresses, and eventually the participant chooses the current iObj orientation as the closest to tObj. In the 1^st and 2^nd tasks, both participants seemed to have progressed in a similar manner, but participant 1 took half as much time as participant 2. And in the 3^rd task, although participant 2 took less time to complete the task, participant 1 had already solved the task before the 20 s mark and kept making small adjustments to better match iObj to tObj. Abbreviation: AD = angular disparity. Please click here to view a larger version of this figure.

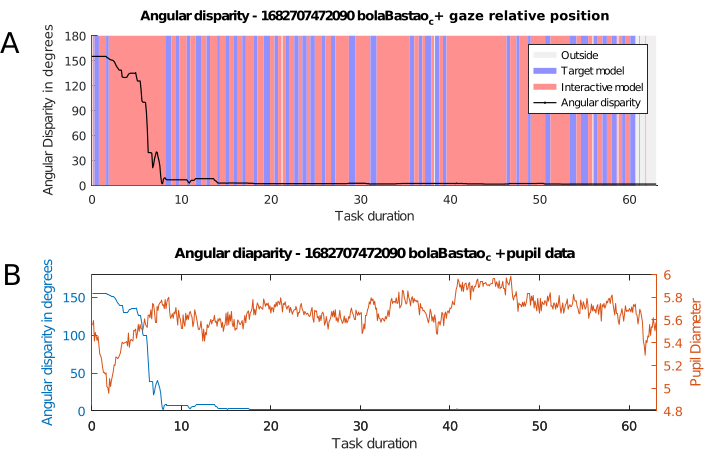
Figure 5: AD with eye-tracking data. Evolution of angular disparity combined with eye-tracker data. (A) Angular disparity and gaze position, theevolution of angular disparity between tObj and iObj, coupled with regional fixation data for each model. The graph shows what region the participant's gaze is located in: red when inside iObj canvas, blue when inside tObj canvas, and gray when outside both of them, looking at another element on the screen or looking away from it. (B) Angular disparity and pupil diameter. Angular disparity, in blue, coupled with pupil diameter data, in orange. Pupil diameter is the mean value of left and right pupils at each point in time. Abbreviation: AD = angular disparity. Please click here to view a larger version of this figure.

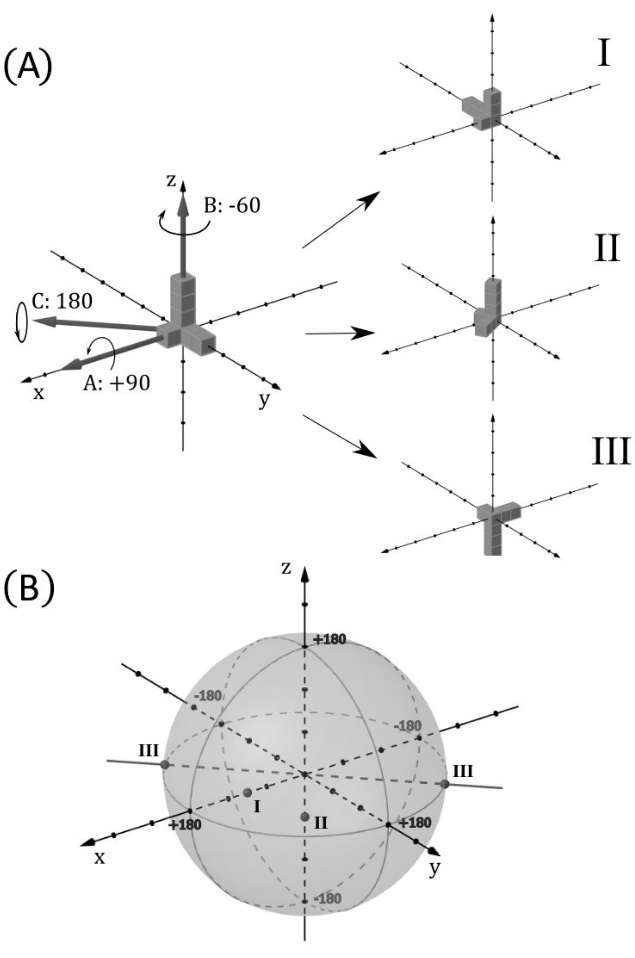
Figure 6: Ball of rotations. This figure illustrates how each possible rotation position of an object from a reference position can be represented as a point in a ball of radius 180°, allowing a complete representation of the object's rotational position in all three axes. Here, a ball is understood as the volume bounded by a sphere. (A) The object used as an example is an asymmetric union of seven cubes, depicted at the top, to the left. Three simple rotations numbered I, II, and III are applied to this object, as shown to the right. They are, respectively, +90° on the x-axis, -60° on the z-axis, and 180° on an axis between +x and -y, at 45° from both axes. (B) The ball of rotation is shown with the points corresponding to the rotations I, II, and III. The distance to the center of the ball is the angle disparity. As III achieves the maximum rotation angle (180°), it is also represented at its antipodal point, as they are essentially the same. Rotation II, being anticlockwise with respect to the positive direction of axis z, appears on the negative side. Please click here to view a larger version of this figure.

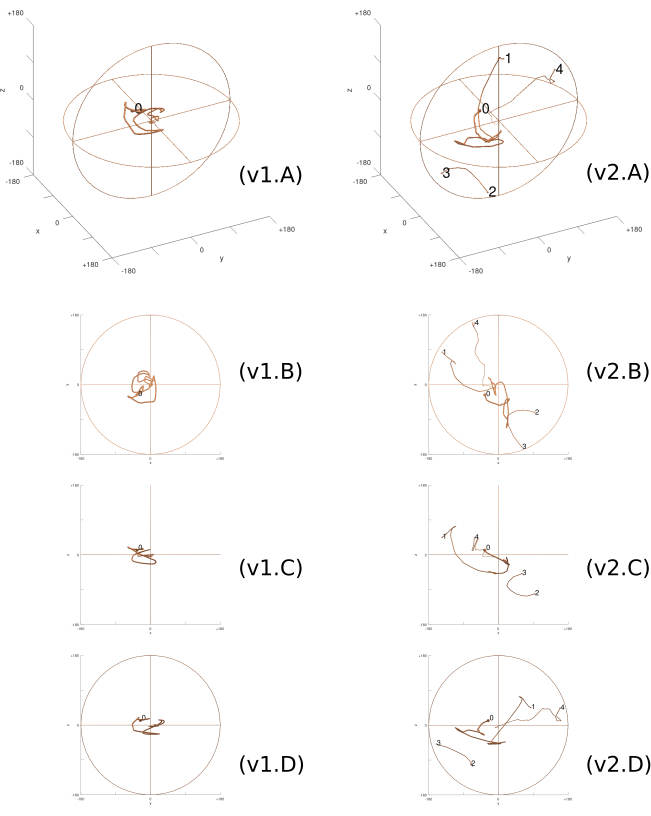
Figure 7: 3D Rotation trajectory. The rotation trajectory inside the ball of rotations taken by the two participants in the third task, viewed both in perspective (A) and in projections on the coordinate planes (B–D). Line thickness decreases over time. Each column corresponds to a participant (v1 and v2). As the trajectories approach the center of the ball, the participants are closer to solving the task. '0' indicates the initial position of the task. Subsequent numbers indicate points where the trajectory reaches the edge of the ball and continues through the antipodal point at the opposite side (1 to 2, 2 to 3, 3 to 4, etc). Please click here to view a larger version of this figure.

Supplemental Table S1: Sheet headers. List of headers in the cloned sheet file. Each header corresponds to a variable name and will receive data from this variable forming a column of values used in the processing and analysis of our data. Please click here to download this File.

Supplemental File 1: Protocol step 1 guide. A list of screenshots guiding through the steps of the protocol method "1. Preparation of data collection tools". Please click here to download this File.

Supplemental File 2: Protocol step 3 guide. A list of screenshots guiding through the steps of the protocol method "3. Data processing and analysis". Please click here to download this File.

Supplemental Video 1: Fixation mapping replay. An example of animated replays of the temporal attention mapping in 3D from iObj and tObj simultaneously. Recorded using OBS Studios and rendered using OpenShot Video Editor. Please click here to download this File.

Discussion

As previously stated, this paper aims to present a detailed procedure of real-time mapping of fixation and saccade motion data on interactive 3D objects, which is easily customizable and only uses software available for free, providing step-by-step instructions to make everything work.

While this experimental setup involved a highly interactive task, such as moving a 3D object to match another object's orientation with PR in two of the three possible axes, we ensured thorough documentation of our scripts through proper commenting to facilitate any customization. Various other types of experiments can be designed, with the eye-tracking device being only one of many other possible devices used for temporal data acquisition.

The headers in the copied file from step 1.1.3.3 define the content and location the data will be collected online. Supplemental Table S1 lists the variable names (all case-sensitive) and their meaning. These variables mirror those found in the JavaScript files within the GitHub repository. The type and variety of data and variable names, both from this sheet and the JavaScript files, should be changed according to the scope and requirements of the research.

The recording of rotation data in quaternions allows the researcher to reproduce the same movements made by the participants during the tasks, facilitating an analysis of the process and using storage space much more efficiently if compared to a screen capture. More detailed analysis, such as 3D rotation trajectory, shown in Figure 7 using the ball of rotations, is only possible through the internal quaternion data of the interactive objects. Expanding from the AD plot over time by Gardony²² and Adams²³, this new type of graph provides more detailed information, with the actual 3D rotation coordinates in time.

Another advantage comes from using a standard time measure to synchronize all data sources. Merging different layers of time-dependent information with this becomes much easier, such as superimposing graphs with multiple data sources, as in Figure 5B with the pupil dilation measurement, or in Figure 5A with colored vertical bands, denoting possible patterns in the participants' solving process, even while there was almost no rotation happening in iObj. The 3D fixation heatmap shown in Figure 3 is only possible from both quaternion data and data synchronization.

It is crucial to use synchronization through a standard time measure to ensure any integration of temporal data. The time standard chosen for our project was the UNIX Epoch, which is used in JavaScript and most other programming languages. Some type of known time standard must be in use for each data set, even if a different standard, which can later, be converted to UNIX Epoch. Temporal data that do not use any standards will most certainly be incapable of synchronization and lose their usefulness.

Another limitation is the relatively low frequency of 10 Hz used in the iRT tests in relation to the eye tracker frequency of 60 Hz. This happens partly due to data processing and transfer limitations within the browser, as any higher frequency used would proportionally reduce the maximum time limit of each task, currently at 327 s. Additionally, smoothly rendering complex animations in Jmol at this framerate already presented challenges. Supplemental Video S1 is a video recording of Jmol rendering a replay with the change of opacity in time, mapping the amount of focus each vertex received. While the video duration is almost 2 min, the actual task was completed in 63 s. Future software developments catered specifically to such functionalities instead of adapting existing ones, could address these limitations and enhance data collection and analysis capabilities.

Disclosures

The authors have nothing to disclose.

Acknowledgements

The authors are thankful to the Coordination for the Improvement of Higher Education Personnel (CAPES) – Finance Code 001 and the Federal University of ABC (UFABC). João R. Sato received financial support from the São Paulo Research Foundation (FAPESP, Grants Nos. 2018/21934-5, 2018/04654-9, and 2023/02538-0).

Materials

Firefox	Mozilla Foundation (Open Source)	Any updated modern browser that is compatible with WebGL (https://caniuse.com/webgl), and in turn with Jmol, can be used
GNU Octave	Open Source	https://octave.org/
Google Apps Script	Google LLC	script.google.com
Google Sheets	Google LLC	https://www.google.com/sheets/about/
Laptop		Any computer that can run the eye tracking system software.
Mangold Software Suite	Mangold	Software interface used for the Eye tracking device. Any Software that outputs the data with system time values can be used.
Mouse		Any mouse capable of clicking and dragging with simple movements should be compatible. Human interfaces analogous to a mouse with the same capabilities, such as a touchscreen or pointer, should be compatible, but may behave differently.
Vt3mini	EyeTech Digital Systems	60 Hz. Any working Eye Tracking device should be compatible.

References

Spearman, C. 34;General intelligence," objectively determined and measured. The American Journal of Psychology. 15, 201-292 (1904).
McGee, M. G. Human spatial abilities: psychometric studies and environmental, genetic, hormonal, and neurological influences. Psychological bulletin. 86 (5), 889-918 (1979).
Johnson, W., Bouchard, T. J. The structure of human intelligence: It is verbal, perceptual, and image rotation (VPR), not fluid and crystallized. Intelligence. 33 (4), 393-416 (2005).
Hegarty, M. Components of spatial intelligence. Psychology of Learning and Motivation. 52, 265-297 (2010).
Uttal, D. H., et al. The malleability of spatial skills: a meta-analysis of training studies. Psychological Bulletin. 139 (2), 352-402 (2013).
Linn, M. C., Petersen, A. C. Emergence and characterization of sex differences in spatial ability: a meta-analysis. Child Development. 56 (6), 1479-1498 (1985).
Johnson, S. P., Moore, D. S. Spatial thinking in infancy: Origins and development of mental rotation between 3 and 10 months of age. Cognitive Research: Principles and Implications. 5, 10 (2020).
Wai, J., Lubinski, D., Benbow, C. P. Spatial ability for STEM domains: aligning over 50 years of cumulative psychological knowledge solidifies its importance. Journal of Educational Psychology. 101 (4), 817-835 (2009).
Newcombe, N. S., Stieff, M. Six myths about spatial thinking. International Journal of Science Education. 34, 955-971 (2012).
Kell, H. J., Lubinski, D., Benbow, C. P., Steiger, J. H. Creativity and technical innovation: spatial ability’s unique role. Psychological Science. 24 (9), 1831-1836 (2013).
Geary, D. C. Spatial ability as a distinct domain of human cognition: An evolutionary perspective. Intelligence. 101616, (2022).
Shepard, R., Metzler, J. Mental rotation of three-dimensional objects. Science. 171, 701-703 (1971).
Shepard, R., Judd, S. Perceptual illusion of rotation of three-dimensional objects. Science. 191, 952-954 (1973).
Just, M. A., Carpenter, P. A. Eye fixations and cognitive processes. Cognitive Psychology. 8, 441-480 (1976).
Just, M. A., Carpenter, P. A. Cognitive coordinate systems: accounts of mental rotation and individual differences in spatial ability. Psychological Review. 92 (2), 137-172 (1985).
Shepard, S., Metzler, D. Mental rotation: effects of dimensionality of objects and type of task. Journal of Experimental Psychology: Human Perception and Performance. 14 (1), 3-11 (1988).
Biederman, I., Cooper, E. Size invariance in visual object priming. Journal of Experimental Psychology: Human Perception and Performance. 18, 121-133 (1992).
Wexler, M., Kosslyn, S. M., Berthoz, A. Motor processes in mental rotation. Cognition. 68 (1), 77-94 (1998).
Wohlschläger, A., Wohlschläger, A. Mental and manual rotation. Journal of Experimental Psychology: Human Perception and Performance. 24 (2), 397-412 (1998).
Jordan, K., W, T., Heinze, H., Peters, M., Jäncke, L. Women and men exhibit different cortical activation patterns during mental rotation tasks. Neuropsychologia. 40, 2397-2408 (2002).
Jansen-Osmann, P., Heil, M. Suitable stimuli to obtain (no) gender differences in the speed of cognitive processes involved in mental rotation. Brain and Cognition. 64, 217-227 (2007).
Gardony, A. L., Taylor, H. A., Brunyé, T. T. What does physical rotation reveal about mental rotation. Psychological Science. 25 (2), 605-612 (2014).
Adams, D. M., Stull, A. T., Hegarty, M. Effects of mental and manual rotation training on mental and manual rotation performance. Spatial Cognition & Computation. 14 (3), 169-198 (2014).
Griksiene, R., Arnatkeviciute, A., Monciunskaite, R., Koenig, T., Ruksenas, O. Mental rotation of sequentially presented 3D figures: sex and sex hormones related differences in behavioural and ERP measures. Scientific Reports. 9, 18843 (2019).
Jansen, P., Render, A., Scheer, C., Siebertz, M. Mental rotation with abstract and embodied objects as stimuli: evidence from event-related potential (ERP). Experimental Brain Research. 238, 525-535 (2020).
Noll, M. Early digital computer art at Bell Telephone Laboratories, Incorporated. Leonardo. 49 (1), 55-65 (2016).
Vandenberg, S. G., Kuse, A. R. Mental rotations, a group of three-dimensional spatial visualization. Perceptual and Motor Skills. 47, 599-604 (1978).
Hegarty, M. Ability and sex differences in spatial thinking: What does the mental rotation test really measure. Psychonomic Bulletin & Review. 25, 1212-1219 (2018).
Kozaki, T. Training effect on sex-based differences in components of the Shepard and Metzler mental rotation task. Journal of Physiological Anthropology. 41, 39 (2022).
Bartlett, K. A., Camba, J. D. Gender differences in spatial ability: a critical review. Educational Psychology Review. 35, 1-29 (2023).
Jansen, P., Schmelter, A., Quaiser-Pohl, C. M., Neuburger, S., Heil, M. Mental rotation performance in primary school age children: Are there gender differences in chronometric tests. Cognitive Development. 28, 51-62 (2013).
Techentin, C., Voyer, D., Voyer, S. D. Spatial abilities and aging: a meta-analysis. Experimental Aging Research. 40, 395-425 (2014).
Guillot, A., Champely, S., Batier, C., Thiriet, P., Collet, C. Relationship between spatial abilities, mental rotation and functional anatomy learning. Advances in Health Sciences Education. 12, 491-507 (2007).
Voyer, D., Jansen, P. Motor expertise and performance in spatial tasks: A meta-analysis. Human Movement Science. 54, 110-124 (2017).
Peters, M., et al. A redrawn Vandenberg and Kuse mental rotations test: different versions and factors that affect performance. Brain and Cognition. 28, 39-58 (1995).
Peters, M., Battista, C. Applications of mental rotation figures of the Shepard and Metzler type and description of a mental rotation stimulus library. Brain and Cognition. 66, 260-264 (2008).
Wiedenbauer, G., Schmid, J., Jansen-Osmann, P. Manual training of mental rotation. European Journal of Cognitive Psychology. 19, 17-36 (2007).
Jost, L., Jansen, P. A novel approach to analyzing all trials in chronometric mental rotation and description of a flexible extended library of stimuli. Spatial Cognition & Computation. 20 (3), 234-256 (2020).
Amorim, M. A., Isableu, B., Jarraya, M. Embodied spatial transformations:" body analogy" for the mental rotation of objects. Journal of Experimental Psychology: General. 135 (3), 327 (2006).
Bauer, R., Jost, L., Günther, B., Jansen, P. Pupillometry as a measure of cognitive load in mental rotation tasks with abstract and embodied figures. Psychological Research. 86, 1382-1396 (2022).
Heil, M., Jansen-Osmann, P. Sex differences in mental rotation with polygons of different complexity: Do men utilize holistic processes whereas women prefer piecemeal ones. The Quarterly Journal of Experimental Psychology. 61 (5), 683-689 (2008).
Larsen, A. Deconstructing mental rotation. Journal of Experimental Psychology: Human Perception and Performance. 40 (3), 1072-1091 (2014).
Ho, S., Liu, P., Palombo, D. J., Handy, T. C., Krebs, C. The role of spatial ability in mixed reality learning with the HoloLens. Anatomic Sciences Education. 15, 1074-1085 (2022).
Foster, D. H., Gilson, S. J. Recognizing novel three-dimensional objects by summing signals from parts and views. Procedures of the Royal Society London B. 269, 1939-1947 (2002).
Stieff, M., Origenes, A., DeSutter, D., Lira, M. Operational constraints on the mental rotation of STEM representations. Journal of Educational Psychology. 110 (8), 1160-1174 (2018).
Moen, K. C., et al. Strengthening spatial reasoning: elucidating the attentional and neural mechanisms associated with mental rotation skill development. Cognitive Research: Principles and Implications. 5, 20 (2020).
Guay, R. B. Purdue spatial visualization test: Rotations. Purdue Research Foundation. , (1976).
Bodner, G. M., Guay, R. B. The Purdue Visualization of Rotations Test. The Chemical Educator. 2 (4), 1-17 (1997).
Maeda, Y., Yoon, S. Y., Kim-Kang, K., Imbrie, P. K. Psychometric properties of the Revised PSVT:R for measuring First Year engineering students’ spatial ability. International Journal of Engineering Education. 29, 763-776 (2013).
Sorby, S., Veurink, N., Streiner, S. Does spatial skills instruction improve STEM outcomes? The answer is ‘yes’. Learning and Individual Differences. 67, 209-222 (2018).
Khooshabeh, P., Hegarty, M. Representations of shape during mental rotation. AAAI Spring Symposium: Cognitive Shape Processing. , 15-20 (2010).
Wetzel, S., Bertel, S., Creem-Regehr, S., Schoning, J., Klippel, A. . Spatial cognition XI. Spatial cognition 2018. Lecture Notes in Computer Science. 11034, 167-179 (2018).
Jost, L., Jansen, P. Manual training of mental rotation performance: Visual representation of rotating figures is the main driver for improvements. Quarterly Journal of Experimental Psychology. 75 (4), 695-711 (2022).
Irwin, D. E., Brockmole, J. R. Mental rotation is suppressed during saccadic eye movements. Psychonomic Bulletin & Review. 7 (4), 654-661 (2000).
Moreau, D. The role of motor processes in three-dimensional mental rotation: Shaping cognitive processing via sensorimotor experience. Learning and Individual Differences. 22, 354-359 (2021).
Kosslyn, S. M., Ganis, G., Thmpson, W. L. Neural foundations of imagery. Nature Reviews Neuroscience. 2, 635-642 (2001).
Guo, J., Song, J. H. Reciprocal facilitation between mental and visuomotor rotations. Scientific Reports. 13, 825 (2023).
Nazareth, A., Killick, R., Dick, A. S., Pruden, S. M. Strategy selection versus flexibility: Using eye-trackers to investigate strategy use during mental rotation. Journal of Experimental Psychology: Learning, Memory, and Cognition. 45 (2), 232-245 (2019).
Montag, M., Bertel, S., Koning, B. B., Zander, S. Exploration vs. limitation – An investigation of instructional design techniques for spatial ability training on mobile devices. Computers in Human Behavior. 118, 106678 (2021).
Tang, Z., et al. Eye movement characteristics in a mental rotation task presented in virtual reality. Frontiers in Neuroscience. 17, 1143006 (2023).
Münzer, S. Facilitating recognition of spatial structures through animation and the role of mental rotation ability. Learning and Individual Differences. 38, 76-82 (2015).
Gardony, A. L., Eddy, M. D., Brunyé, T. T., Taylor, H. A. Cognitive strategies in the mental rotation task revealed by EEG spectral power. Brain and Cognition. 118, 1-18 (2017).
Ruddle, R. A., Jones, D. M. Manual and virtual rotation of three-dimensional object. Journal of Experimental Psychology: Applied. 7 (4), 286-296 (2001).
Sundstedt, V., Garro, V. A Systematic review of visualization techniques and analysis tools for eye-tracking in 3D environments. Frontiers in Neuroergonomics. 3, 910019 (2022).
Sawada, T., Zaidi, Q. Rotational-symmetry in a 3D scene and its 2D image. Journal of Mathematical Psychology. 87, 108-125 (2018).
Xue, J., et al. Uncovering the cognitive processes underlying mental rotation: an eye-movement study. Scientific Reports. 7, 10076 (2017).
O’Shea, R. P. Thumb’s rule tested: Visual angle of thumb’s width is about 2 deg. Perception. 20, 415-418 (1991).
Todd, J., Marois, R. Capacity limit of visual short-term memory in human posterior parietal cortex. Nature. 428, 751-754 (2004).

Automatically Generated